matlab内部迭代函数_MATLAB：向量化编程提升值函数迭代（Value Function Iteration）的速度...

作者: 王美庭
Email: wangmeiting92@gmail.com
参考资料：我们高宏王彬老师的讲义

考虑以下贝尔曼方程：

迭代思想为：

直至值函数收敛。在编程时，我们需要对函数进行离散化。于是令

构建 矩阵：

该矩阵第 行的最大值即为 ，从而可得到下一期的 。依此类推，即可构建出值函数迭代的编程过程。最开始时，我们可能会考虑使用循环来得到 矩阵，这在思维上是比较清晰易懂、在编程中也是比较好操作的，代码可能如下：

vkk = zeros(N,N);               
 for i=1:N
     for j=1:N
         if A*k(i)^alpha-k(j)<=1e-5
             vkk(i,j) = -1e5; %如果消费为负，则使其不会被选中
         else
             vkk(i,j)= log(A*k(i)^alpha-k(j))+beta*v0(j);
         end
     end
 end

但这可能在运算上花费大量时间。如果我们采用向量化编程，代码可能如下(读者自己可以doc其中自己不太清楚的命令来理解其中的编程思想，其实这里仅仅是额外用到了repmat函数)：

ckk = repmat(A*k.^alpha,1,N) - repmat(k',N,1);
ckk(ckk<1e-5) = 1e-10;
lckk = log(ckk);
lckk(lckk<-23) = -1e5;
vkk = lckk + beta*repmat(v0',N,1);

如果是 stochastic 的情况，那你可能还需用到 permute和reshape函数。

在下方的测试代码中，向量化编程求解的速度将是循环求解的 10 倍左右。这里只是一个简单的练习，如果是 stochastic 的情况，情况会更复杂，可能会涉及到多维矩阵的构建，这时你可能需要花很多的时候来保证不出错，但是，为了后期计算速度的提升，这往往是值得的。下面附上全部代码以及运算结果图像：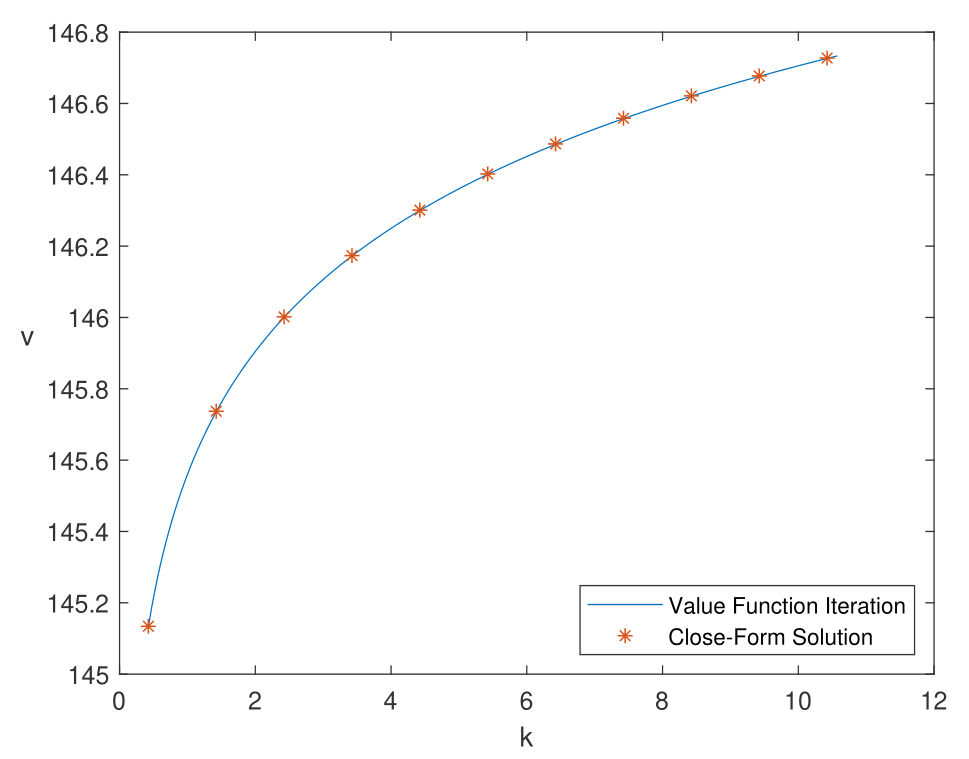

%=========================================================================
% Chapter 2
% File: vfi_wmt.m
% Purpose: solve the infinite optimal growth model
% Method: value function iteration
% Update: January 18, 2021
% Written by Meiting Wang
%=========================================================================

tic
clear all;
close all;
clc;


%% parameters
A = 5;
alpha = 1/3;
beta = 0.99;
kbar = (A*alpha*beta)^(1/(1-alpha));
k = [1/5*kbar:0.05:5*kbar]';
N = length(k);
v0 = zeros(N,1);
d0 = zeros(N,1);
tol = 1e-5;
maxI = 1e5;
diff = 2;

it = 0;  %counter of iteration


%% value function iteration
while (diff >= tol) & (it <= maxI)
    if mod(it,100) == 0
       fprintf('Iteration: %4.0f    diff: %.3en',it,diff);
    end
    
    ckk = repmat(A*k.^alpha,1,N) - repmat(k',N,1);
    ckk(ckk<1e-5) = 1e-10; %make ln(ckk) meaningful
    lckk = log(ckk);
    lckk(lckk<-23) = -1e5; %make values that consume too little will not be selected
    vkk = lckk + beta*repmat(v0',N,1); %get the vkk matrix
    
    %Get the value function and policy function in the next period
    [v1,d1] = max(vkk,[],2);
    diff = max(abs(v1-v0));
    v0 = v1;
    d0 = d1;
    it = it + 1;
end

if diff    disp('Value function iteration succeeds');
   fprintf('Iteration: %4.0f    diff: %.3en',it,diff);
else
    disp('Value function iteration fails');
    fprintf('Iteration: %4.0f    diff: %.3en',it,diff);
end

% Output the mean and variance of v0 and d0.
fprintf('MEAN of v0: %7.3f       VAR of v0: %7.3fn',mean(v0),var(v0))
fprintf('MEAN of d0: %7.3f       VAR of d0: %7.3fn',mean(d0),var(d0))
toc


%% graph
% Value Function
E = 1/(1-beta)*(log(A*(1-alpha*beta))+alpha*beta/(1-alpha*beta)*log(alpha*beta*A));
F = alpha/(1-alpha*beta);
v_closed = E + F*log(k);

figure;
P = plot(k,v0,'-',...
    k,v_closed,'*');
P(2).MarkerIndices = 1:20:length(k);
xlabel('k');
ylab = ylabel('v   ');
ylab.Rotation = 0;
legend({'Value Function Iteration','Close-Form Solution'},...
    'Location','southeast','NumColumns',1)
saveas(gcf,'1_1','pdf')

% Policy Function
k_prime_closed = A*alpha*beta*k.^alpha;

figure;
P = plot(k,k(d0),'-',...
    k,k_prime_closed,'*');
P(2).MarkerIndices = 1:20:length(k);
xlabel('k');
ylab = ylabel("k^{prime}   ");
ylab.Rotation = 0;
axis equal;
xlim([0 11]);
ylim([1 4]);
legend({'Value Function Iteration','Close-Form Solution'},...
    'Location','southeast','NumColumns',1)
saveas(gcf,'1_2','pdf')

% Saddle Path
c = A*k.^alpha - k(d0);

figure;
plot(k,c,'-',...
    [kbar kbar],[0 12],'-',...
    0:0.02:12,A*(0:0.02:12).^alpha-(0:0.02:12),'-');
xlabel('k');
ylab = ylabel('c  ');
ylab.Rotation = 0;
xlim([0 12]);
ylim([0 12]);
legend({'Saddle Path',...
    '$bar{k}=(Aalphabeta)^{frac{1}{1-alpha}}, Delta c_{t+1}=0$',...
    '$c_t = Ak_t^alpha - k_t, Delta k_{t+1}=0$'},...
    'Location','northeast','NumColumns',1,'interpreter','latex')
saveas(gcf,'1_3','pdf')