[基因遗传算法]进阶之二:最优规划问题--多种编码方式+多变量

74 阅读 0 评论 49 点赞

我是靠谱客的博主轻松鞋垫，最近开发中收集的这篇文章主要介绍[基因遗传算法]进阶之二:最优规划问题--多种编码方式+多变量，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

参考资料:
《遗传算法求解带约束优化问题（源码实现》
《有约束的遗传算法（Python代码实现）》
《遗传算法原理及其python实现》

同系列文章:
《[基因遗传算法]原理思想和python代码的结合理解之(一) :单变量》

解决的问题:线性规划最优解的问题. 可以应用在运筹学,优化问题, 最优传输理论的离散问题,深度学习中. 对于较简单的问题,应用广泛.
解决问题案例:
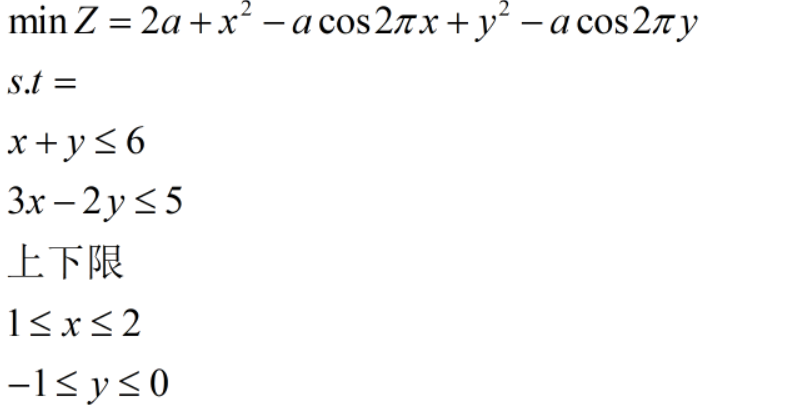
在这里插入图片描述

目标函数:最小化. 如果求最大值,目标函数添加负号-
不等式约束条件: 以小于号 $\leq$ 为主.If $\geq$ ,添加负号-,转化形态.
自变量范围: 有两个自变量 $x, y$ .分别具有自己的上下限,且好处是自变量的范围是连续的.

一、个体与种群

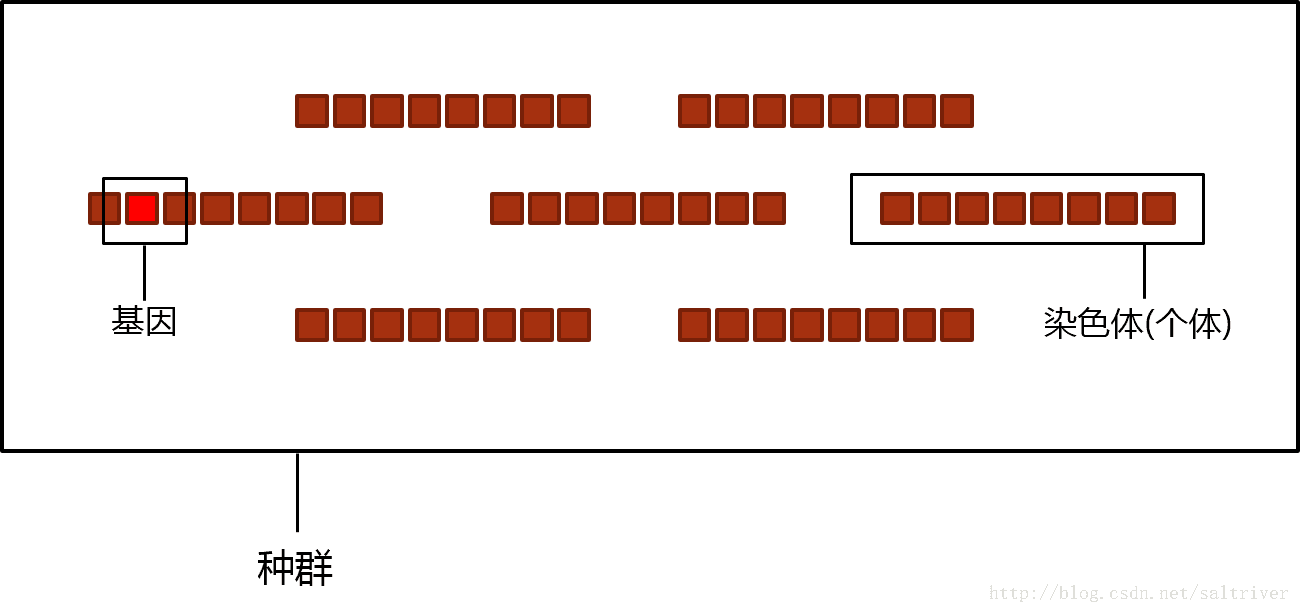
在这里插入图片描述

Fig.1 种群,个体,基因的关系

A. 个体的编码问题

在前一篇,我们采用了二进制编码的方式.其好处在于做交叉、变异的时候,代码写的非常舒服(便利).但同时其缺点明显.如果 $x$ 的定义域范围更广,要求精度更细.则其DNA的长度(存储单位)则会更长.因此对于个体编码有二进制编码、格雷编码、实数编码、符号编码。,具体可见:《万字字符长文带你了解遗传算法（有几个算例源码）》

不同的编码对应于不同的交叉和变异的代码书写思路.

B. 实数编码的交叉和变异的思路(单变量)

以上一篇的目标函数 $y = 10 \cdot s i n (5 x) + 7 \cdot c o s (4 x)$ ,定义域 $x \in [0, 5]$ 为例.

NP=5
pop=np.random.uniform(0, 5,(NP,))# 实数编码
pop

结果:
array([4.10882862, 4.50177413, 1.63557154, 3.38813064, 2.84975806])
交叉的某种方式: 节选父与母的一部分.

def crossover(parent1,parent2):
if np.random.rand() < PC:
#交叉概率
gamma=round(np.random.rand(),2)#随机产生一个(0,1)浮点数,并保留2位小数
parent1=gamma*parent1+(1-gamma)*parent2
return parent1

变异的某种方式:重新实数赋值

def mutation(child):
# 用随机赋值的方式进行变异
if np.random.rand() < PM:#变异概率
child= np.random.uniform(0,5)#重新随机赋值
return child

种群的交叉和变异:

pop_copy=pop.copy()
for i in range(NP):
#parent1=pop[i]
parent2=pop_copy[np.random.randint(NP)]# 随机产生父母2
child=crossover(pop[i],parent2)#交叉
pop[i]=mutation(child) #变异
pop

结果:
array([3.63316795, 4.50177413, 1.63557154, 3.38813064, 3.78147027])

二、多变量的问题

以目标函数 $Z=2a+x^2-acos2πx+y^2-acos2πy$ 求最小值为例. $x \in [- 5, 5], y \in [- 5, 5], a = 10$ .
当多变量的时候,相当于个体具有多条染色体,对应的染色体(表示相同特征,或说对应同一个自变量)之间才能交叉.

A.多变量的目标函数书写

def fitness_func(X):
# 目标函数，即适应度值，X是种群的表现型
a = 10
pi = np.pi
x = X[:, 0]
y = X[:, 1]
return 2 * a + x ** 2 - a * np.cos(2 * pi * x) + y ** 2 - a * np.cos(2 * 3.14 * y)

B. 二进制的编码的交叉和变异思路(多变量)

NP=5 #种群数量
DNA_SIZE=4#DNA长度,应设为20,为方便看结果缩小的
DNA_NUM=2#染色体个数
pop= np.random.randint(0, 2, (NP, DNA_SIZE*DNA_NUM))
# 随机初始化种群，为50*40的0-1矩阵
pop

结果:
在这里插入图片描述
解码方式

对单条染色体解码

def decode(x, a, b):
"""解码，即基因型到表现型,同单变量相同"""
xt = 0
for i in range(len(x)):
xt = xt + x[i] * np.power(2, i)
return a + xt * (b - a) / (np.power(2, len(x)) - 1)
# 或者
def decode(x, a, b):
"""解码，即基因型到表现型"""
DNA_SIZE=len(x)
x_d=x.dot(2 ** np.arange(DNA_SIZE)[::-1]) *(b-a)/ float(2**DNA_SIZE-1) +a
return x_d

对个体(多条染色体)解码

def decode_X(pop: np.array,lb,ub):
"""
对整个种群的基因解码，上面的decode是对某个染色体的某个变量进行解码
pop:种群(二进制基因)
lb: 变量的下限列表
ub: 变量的上限列表
"""
X =np.zeros((NP,n_dim))#解码后的种群的变量值存储,(5,2)
indivi=np.zeros(n_dim)
for i in range(NP):
for j in range(n_dim):
x =decode(pop[i,DNA_SIZE*j:DNA_SIZE*(j+1)],lb[j],ub[j])
#xi = decode(pop[i, :20], -5, 5)
indivi[j]=x
X[i, :] = indivi
return X

解码计算:

NP=5
DNA_SIZE=20#设为20
n_dim=2
pop= np.random.randint(0, 2, (NP, DNA_SIZE*n_dim))
lb=[-5,-5]
ub=[5,5]
X = decode_X(pop,lb,ub)
X

结果为:
array([[ 2.06021982, -0.35688911],
[ 2.00679494, -3.61610281],
[-4.44379753, -4.92298119],
[ 4.34191641, 4.12501252],
[-4.70489474, -0.42363684]])
(多变量)交叉与变异
与(单变量)二进制的交叉与变异类似,只是在外面多加了一套染色体个数的循环.

C.使用`sko.GA`解决问题

def aim(p):
a = 10
pi = np.pi
x,y=p
return 2 * a + x ** 2 - a * np.cos(2 * pi * x) + y ** 2 - a * np.cos(2 * 3.14 * y)
ga = GA(func=aim, n_dim=2, size_pop=50, max_iter=1000,
lb=[-5,-5], ub=[5,5], precision=1e-7)
best_result= ga.run()
print(best_result)