摘要

数据驱动范式是未来无线通信的众所周知且突出的需求。在大数据和机器学习技术的支持下，下一代数据驱动的通信系统将智能化，具有表达性、可扩展性、可解释性和不确定性感知等独特特性，在可预见的未来可以自信地涉及多样化的潜在需求和个性化服务。在本文中，我们回顾了一系列有前途的非参数贝叶斯机器学习模型，即高斯过程 (GPs)，以及它们在无线通信中的应用。由于GP模型在不确定的情况下表现出杰出的表现力和可解释的学习能力，它们特别适合于无线通信。此外，它们为协作数据和经验模型（DEM）提供了一个自然框架。具体来说，我们首先设想了使用GP模型的数据驱动的无线通信的三个层次的动机。然后，我们在协方差结构和模型推理方面介绍了GPs的背景。展示了使用各种可解释内核 (包括固定，非固定，深度和多任务内核) 的GP模型的表现力。此外，我们回顾了具有良好可扩展性的分布式GP模型，它适用于具有大量分布式边缘设备的无线网络中的应用。最后，我们列出了在各种无线通信应用中采用GP模型的代表性解决方案和有前途的技术。

关键词：无线通信；高斯过程；机器学习；核心;可解释性；不确定

I 简介

  最近，在用于无线通信的人工智能 (AI) 方面经历了爆炸式增长 [1-6]。此外，基于数学建模的传统范式 (TPs) 极大地阻碍了未来无线通信的发展，并对其新兴应用产生了负面影响，例如车联网 (IoV) [7-9]、物联网 (IoT) [10] –14]、增强/虚拟现实 (AR/VR) [15, 16] 和节能 5G [17-21]。许多新型智能互联传感器和人工智能应用越来越依赖智能实时响应和可解释的决策，例如自动驾驶汽车的紧急制动、无人机的障碍物预警、智能制造的故障诊断、环境感知用于协作多机器人系统，以及用于 AR/VR 的可预测人机交互，以减少响应时间和人为干预。这些应用程序驱动的需求要求下一代通信系统 [22-24] 具有以下受欢迎的功能: 灵活性，可扩展性，可解释性，尤其是不确定性建模，以自信地涉及潜在需求和未来的个性化服务。

  与无线通信中的传统范例相比，机器学习的一个显著优势是其获取知识和自动提取信息的能力，而不需要特定的规则[25]。然而，由于对状态预测的解释不足，黑箱决策的机器学习方法[26-28]总是混淆复杂通信系统的诊断和分析，并导致对其运行机制的被动理解。为了促进数据驱动无线通信的可解释机器学习，在本文中，我们回顾了高斯过程（GP）模型，并展示了它们在无线通信中的应用，因为它们具有不确定性的可解释学习能力。

  GP 是高斯概率分布的推广，这意味着 GP 是函数 $f(\mathbf{x})$ 上的任何分布，因此任何有限的函数值集都具有联合高斯分布 [25, 27]。GP 提供了一个模型，在该模型中，随着证据的积累，未知函数的后验分布得以保持。这使得 GPs 能够在收集大量观测数据时了解无线通信系统的基本功能。与流行的深度神经网络 (DNN) [31] 和其他学习模型相比，GP 模型显示出不确定性限定的独特属性，其封闭式的数学表达对要求可控和可理解的状态预测的数据驱动的无线系统有很大价值。在表 1 中，我们将 GP 与 DNN、强化学习 (RL) 和 TP 在模型表达性、可解释性、可扩展性、不确定性建模、样本效率以及数据和经验模型 (DEM) 的协作方面进行了比较。

1.1 相关工作

  GP可以通过设计其协方差函数（也称为核函数）来模拟一个庞大而复杂的无线通信系统，该函数编码了一个对未知函数的自动协方差的假设。因此，内核在GP模型中是至关重要的，因为它意味着函数上的分布特征。此外，可扩展推理是 GP 的另一个核心方面，因为对于大规模无线通信系统，GP 的计算复杂度是 $\mathcal{O}(n^3)$。这通常会阻止GP学习大数据问题。因此，使用GPs的无线通信最重要的进展与核函数设计和可扩展推理这两个方面有关，这两个方面得到了广泛的研究[2, 35, 36, 34]。有许多教程和调查工作回顾了无线通信中的 GP，例如 [2, 37]。在最近的一篇杂志论文[2]中，介绍了GP模型作为传统深度学习模型的替代品，以解决下一代数据驱动的无线通信系统的关键不确定性问题，然而，GP模型的技术细节被保留下来。在杂志论文[37]中，介绍了用于非线性信号处理的GP模型。其中，提出了用于无线通信的信号处理的许多说明性应用，例如概率信道均衡和非线性信道变化的跟踪。[37]的主要关注点在于展示GP模型优越的非线性映射能力，而不是模型的表达能力和可解释性。相比之下，我们的调查论文既全面概述了近年来发展的数学进步，又全面调查了受益于使用 GP 模型的无线通信应用。

  通常，对于核函数设计，在GP的现有工作中大致有四类协方差设计，包括

• 组合内核设计 [38, 39]，其中内核由几个现有的基本内核组合构建；
• 谱核学习，其中核是通过将核谱密度建模为分布的混合而得出的[40-43]；
• 深度核表示 [44,45]，其中DNN在输入空间和特征空间之间的非线性映射中起作用；
• 多任务内核[46, 47]，相邻的设备（任务）分享知识并相互作用，以获得集体智慧。

在接下来的部分中，我们将详细回顾相关工作。

  为了克服大规模无线通信系统中使用的GP [2,27，34,48] 的计算复杂性问题，可以通过探索来实现可扩展的推理(1) 低秩协方差矩阵逼近 [49,50]，(2) 核矩阵的特殊结构 [51,52]，(3) Bayesian committee machine (BCM)，它将计算分配给大量的计算单元 [53,54]，(4) 变分贝叶斯推理 [55, 56]，和 (5) 特殊优化 [57, 43]。 值得注意的是，这些可扩展的方法不是排他性的，我们可以结合其中的一些来获得更好的方法，例如，随机变分推理 (SVI) [55,56] 结合了低秩近似和变分推理的诱导点的强度。

1.2 大纲

  本次调查的主要贡献总结如下：

• 我们广泛讨论了下一代数据驱动的无线通信系统普遍期望的 AI 特性，即表现力、可扩展性、可解释性和不确定性建模。关于这些方面，我们将 GP 与其他机器学习方法进行比较，然后得出结论 GP 可以更好地覆盖这些品质（如表 1 所示）。

• 我们从数学定理和GP核表达式的角度对协方差设计进行了广泛的分析和解释，包括 (1) 平稳核，(2) 非平稳核，(3) 深度核和 (4) 多任务核。这些内核在无线通信中利用了GP模型的表现力和可解释性。

• 由于无线通信系统的可扩展性需求和分布式部署，我们回顾和评估了分布式 GP 在云智能大数据和支持 AI 的边缘设备中的可扩展推理的进展。

• 我们通过推断从现实世界的5G无线基站收集到的5G在线用户数，展示了一个示范性案例。结果显示了GPs对于数据驱动的无线通信的可表达性、可解释性和不确定性建模。

• 我们展示了一些应用GP模型的代表性无线通信场景，并进一步设想了在未来数据驱动的无线通信中使用GP的一些开放问题和挑战。

  对于本文的其余部分，我们首先在第二节中介绍使用GPs进行数据驱动的无线通信的动机，然后在第三节中给出GPs的数学背景。在第四节和第五节中，我们介绍了GPs的进展。第六节给出了使用GPs进行无线通信的演示。在第七节和第八节中，我们分别给出了现有的GP应用和无线通信的未来研究。

II 数据驱动的无线通信: 具有独特功能的动机

  在本节中，我们介绍了使用机器学习方法的下一代数据驱动的无线通信的独特功能，具有可表达性、可扩展性、不确定性建模和可解释性（见表1）。

  由于数据驱动的无线通信系统固有的智能要求，应用 GP 的动机分为三个层次。首先，低层次的动机是基于未来无线通信系统中智能、高效、灵活的决策、规划和预测的需求[3]，这一点是应用传统范式无法实现的。然后，GP与其他机器学习方法的比较带来了中层动机，并全面解释了为什么我们倾向于选择GP模型用于数据驱动的无线通信系统[25、27]。如第 VI 节所示，高级动机来自 GP 在无线通信中授权的竞争应用。具体而言，动机可以概括如下:

• 对于未来的无线通信系统，预期存在许多由多样化应用驱动的潜在需求和个性化服务。随着历史数据的增长和计算能力的不断增强，这些潜在需求和个性化服务可以通过机器学习方法进一步建模和改进。有许多描述未来无线通信的特征：(a) 表现力与模型的复杂性相关，这是多样化应用场景的结果[4, 58]; (b) 由于网络规模随着网络密集化和连接的智能设备数量的增加而不断增长，在大数据上的可扩展性[3, 59]。© 动态通信环境产生的不确定性 [60,61]; 和 (d) 可解释的知识发现和表示，用于理解复杂系统的机制 [62, 63]。特别地，不确定性建模对于无线网络中的状态预测至关重要，因为总是存在多种噪声和动态因素来干预系统的状态和移动用户的体验。

• 作为一类贝叶斯非参数模型，GP为学习内核结构编码的模式提供了一种原则性的、实用的、概率性的方法[27] 。在所有机器学习模型中，GP与各种学习模型有着紧密的联系 [25-27]，包括spline models、支持向量机 (SVMs) 、正则化最小二乘模型、相关向量机 (RVMs) 、自回归移动平均线 (ARMAs) 、和深度神经网络 (DNNs)。特别是，从贝叶斯的角度来看，GPs在模型学习的解释，模型选择和不确定性预测方面具有优势。通过使用合适的内核结构和计算近似，GP可以对无线通信系统的任何功能进行建模，具有灵活性和可扩展性。由于贝叶斯规则，具有不确定性度量的GP对过拟合问题具有更强的鲁棒性。与其他机器学习模型相比，GP 模型可以同时满足数据驱动无线通信的表达性、可扩展性、不确定性建模和可解释性 [25, 27] 的要求。

• 由于贝叶斯属性，GP模型在模型构建、选择和超参数适应方面具有引人注目的解释（见第三节）。这种解释的优势促进了大量的GP模型，以赋予多样化的无线通信应用。有五种流行的 GP 模型使用不同的内核来支持各种无线通信任务，例如具有固定光谱混合物 (SM) [40,64] 和组成核 [65] (见第4.1节) 、非平稳 (NS) 核 [66-69] (见第4.2节) 、深度核 [44,70] (见第4.3节) 的GP模型，和多任务内核 [34,46] (见第4.4节)。此外，GPs具有分布式推理的可扩展性变化，可以在大量的边缘设备上扩展大数据（见第五节）。分布式GPs可以充分利用无线网络中本地边缘设备的计算资源来获得效率的提高以及隐私的保护[35, 71]。

III 用于机器学习的高斯过程的背景

  无线通信建模存在多个不确定性问题：(1) 描述真实函数和学习模型之间差距的函数不确定性； (2) 由观测证据的数量引起的范围模糊的预测不确定性；(3) 由于在无线传播过程中产生的噪声而导致的输入不确定性; 以及 (4) 由于无线传播不稳定和测量传感器精度差而导致的输出不确定性。从理论上讲，这些不确定性以及可解释性可以用 GP 模型很好地表示。在本节中，我们从数学定义、核函数和模型推断等方面简要描述机器学习高斯过程的背景。

3.1 高斯过程的定义

  从函数空间的角度来看，高斯过程[26, 27]定义了一个函数上的分布 $p(f({\mathbf{x}}_1),f({\mathbf{x}}_2),...,f({\mathbf{x}}_n))\sim \mathcal{N}(m(\mathbf{x}),K(\mathbf{x},{\mathbf{x}}^{\prime }))$ ，完全由其一阶和二阶统计指定，即均值 $m(\mathbf{x})$ 和协方差 $K(\mathbf{x},{\mathbf{x}}^{\prime })$ 函数[72]。 对于一个实数随机过程 $f(\mathbf{x})$ 的给定输入位置$x\in {\mathbb{R}}^p$，均值 $m(\mathbf{x})$ 和协方差函数 $K(\mathbf{x},{\mathbf{x}}^{\prime })$ 定义如下:
$$m(\mathbf{x})=\mathbb{E}[f(\mathbf{x})]\text{\hspace{1em}(1a)}$$
$$k(\mathbf{x},{\mathbf{x}}^{\prime })=\mathbb{E}[f(\mathbf{x}-m(\mathbf{x}))(f({\mathbf{x}}^{\prime })-m({\mathbf{x}}^{\prime }))]\text{\hspace{1em}(1b)}$$

  因此，GP 表示为 $f(\mathbf{x})\sim \mathcal{G}\mathcal{P}(m(\mathbf{x}),k(\mathbf{x},{\mathbf{x}}^{\prime }))$。不失一般性，GP 的均值通常在任何地方都被假定为零，因为我们通常没有关于均值的任何先验知识。应用函数值之间的协方差函数（也叫核），在输入点 $X$ 上构建一个正定的协方差矩阵，用于联合高斯分布，这里用格拉姆矩阵 $K=K(X,X)$ 表示。通过在内核指定和参数初始化中使用GP先验函数，我们可以预测测试点 ${\mathbf{x}}_{\ast }$ 的未知函数值 $\stackrel{\sim }{y_{\ast }}$ 及其方差 $\mathbb{V}[y_{\ast }]$（即其不确定性）。具体来说，我们有以下GP回归的预测方程 [27,48]:
$$\stackrel{\sim }{y_{\ast }}={\mathbf{k}}_{\ast }^T(K+{\sigma }_n^{2}I{)}^{-1}\mathbf{y}\text{\hspace{1em}(2a)}$$
$$\mathbb{V}[y_{\ast }]=k({\mathbf{x}}_{\ast },{\mathbf{x}}_{\ast })-{\mathbf{k}}_{\ast }^T(K+{\sigma }_n^{2}I{)}^{-1}{\mathbf{k}}_{\ast }\text{\hspace{1em}(2b)}$$
其中，${\mathbf{k}}_{\ast }^T$ 是 ${\mathbf{x}}_{\ast }$ 和 $X$ 之间的协方差向量，${\sigma }_n^2$ 是噪声的方差，$\mathbf{y}$是与 $X$ 相对应的观测值的向量。

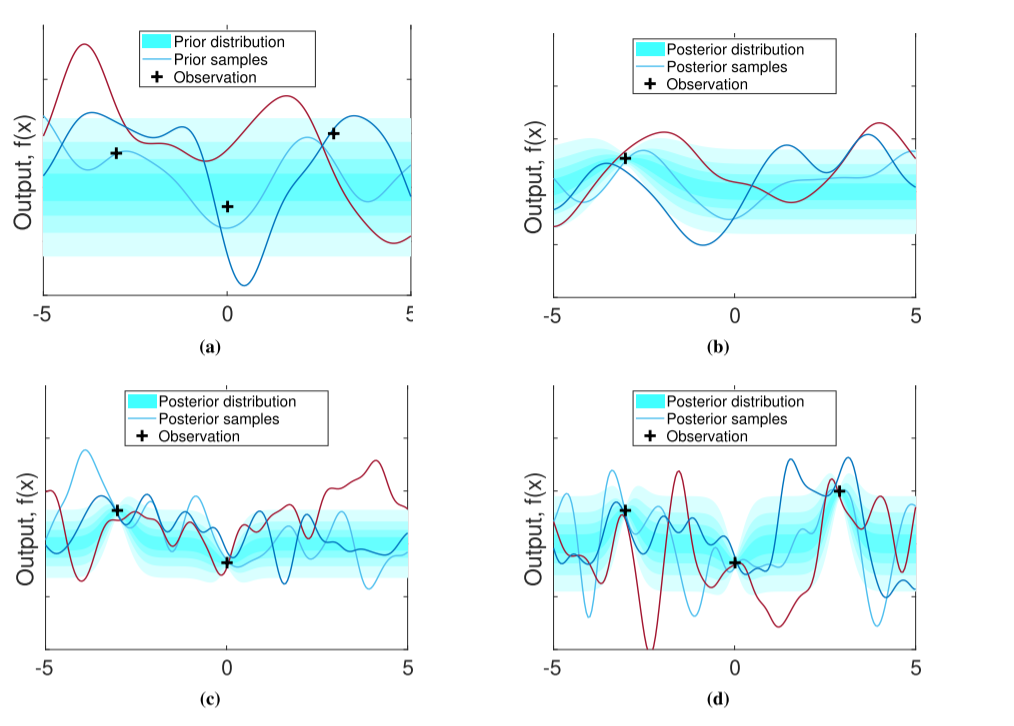
图 1. 基于三个观察（黑色十字）的 GP 先验分布和 GP 后验分布的样本。子图（a）是先验分布（青色）和采样（浅蓝色、深蓝色和红色）；子图 (b)、© 和 (d) 分别是后验分布和采样，分别具有 1 个、2 个和 3 个观测值。阴影区域（青色）可以看作是预测函数值的不确定界限。随着收集到的观察值的增加，GPs 可以非常平滑地适应底层函数空间。

3.2 高斯过程内核(Gaussian Process Kernel)

  基本上，GP的平滑性和泛化性质取决于核函数及其超参数 $\Theta$。选择适当的核函数和相应的初始超参数对于GP设计至关重要，因为后验分布对于不同的核可能会有很大差异。最广泛使用的协方差函数是平稳的。最广泛使用的协方差函数是平稳的。在后面的部分中，我们将介绍平稳和非平稳协方差函数的广义理论。对于要由GP建模的基础函数，有许多特征，例如指数衰减依赖性和周期依赖性，可以通过特定的协方差函数进行编码。

  为了使GP模型适用于实际应用，GP模型的推断也非常重要。在GP模型的推断阶段，即使事先指定了适当的协方差，模型选择的自由度也是相当大的。通常，GPs包含描述内核属性和GP噪声的超参数 $\Theta$。假设我们选择了具有超参数 ${\Theta }_k$ 的协方差函数 $k(\mathbf{x}，\mathbf{x}\prime )$。GP的推论意味着贝叶斯模型选择的可能最佳值为 Θ = { Θ k , σ n 2 } Θ = {Θ_k, σ^2_n} Θ={Θk​,σn2​}。这样的选择可以通过最小化负对数边际似然 (NLML) 来完成，${\mathcal{L}}_{NLML}=-logp(\mathbf{y}|X,\Theta )$。GP模型的推断和后验抽样如图1所示。

  NLML可用于评估GP模型的拟合度。对于GP模型的评估，我们通常使用均方误差（MSE）和平均绝对误差（MAE） 来衡量预测性能。具体来说，公式（2b）中描述的预测不确定性对预测的置信度进行评分。

IV GP内核的进展

4.1 固定谱混合核(Stationary Spectral Mixture Kernel)

   在无线通信系统中生成的数据通常会显示以下模式 :(1)工作日和周末的每周定期趋势。(2) 工作时间和业余时间的日常定期趋势。(3)小范围变化方面的衰减偏差。和（4）一些引入无序波动的噪声。这些模式通常是固定的，可以由具有灵活内核结构的GP捕获（见第六节）。然而，如果没有切实的事先信息，模式的数量和它们的信号特征对于定义和构建GP模型是不明确的。或者，我们可以应用固定内核的通用表示，然后通过优化自动推断潜在模式，这可以简化无线通信系统中机器学习的实践，提高可解释知识发现的效率。

  在本节中，我们回顾了平稳协方差函数的理论基础和最近的 GP 工作。平稳协方差被认为是 $\tau =\mathbf{x}-{\mathbf{x}}^{\prime }$ 的函数，而不是输入位置 $\mathbf{x}$，它对于输入空间中的平移是不变的 [27]。对于平稳过程的每个协方差函数，在频域中都有一个相应的表示形式，即正有限度量 $ψ $ 的傅立叶变换。参考文献[73，74]，Bochner定理指出了协方差函数与其谱密度之间的联系。

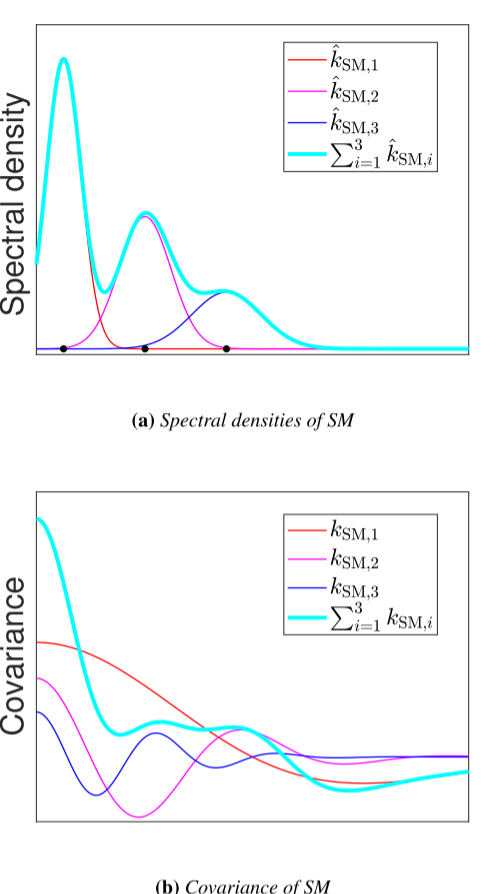
图2 谱密度（左）与高斯混合体和相应的协方差函数（右）在SM核中的谱密度。对于SM，每个分量的位置（黑点）表示功能不足的时期。

Theorem 1 (Bochner’s Theorem [73, 74]). ${\mathbb{R}}^P$上的复值函数 $k$ 是 ${\mathbb{R}}^P$ 上的弱平稳均方连续复值随机过程的协方差函数，当且仅当它可以表示为
$$k(\tau )={\int }_{{\mathbb{R}}^P}{e}^{2\pi ȷs^T\tau }\psi (d\mathbf{s})$$
其中 $\psi$ 是正有限测度并且 $ȷ$ 表示虚数单位。

  如果 $\psi$ 具有称为 $k$ 的谱密度或功率谱的密度 $\hat{k}(\mathbf{s})$，则定理 (1) 意味着以下傅里叶对偶。
$$\{\begin{array}{c}k(\tau )=\int \hat{k}(\mathbf{s})e^{2\pi ȷs^T\tau }d\mathbf{s}\\ \hat{k}(\mathbf{s})=\int k(\tau )e^{2\pi ȷs^T\tau }d\tau \end{array}\text{\hspace{1em}(3)}$$
  基于Bochner定理，提出了大量的表达平稳内核，包括光谱混合内核 (SMs) 和组合式内核。组合式内核[75, 65]有先进的内核结构，通过使用一系列的内核操作，如加法、包法和乘法操作，从普通内核的组合中构建。此外，最具代表性的固定内核之一是SM内核 [40,76，41,77，78]，因为SM可以近似具有足够数量分量的任何固定内核。 这里，我们主要介绍SM核。SM核 $k_{SM}$ 是通过用高斯混合模型（GMM）表示其频谱密度（核的傅里叶变换）而得到的（见图2），${\hat{k}}_{SM}(\mathbf{s})={\sum }_{i=1}^Q{\hat{k}}_{SM,i}(\mathbf{s})$，其中${\hat{k}}_{SM,i}(\mathbf{s})={\omega }_i[{\phi }_{SM,i}(\mathbf{s})+{\phi }_{SM,i}(-\mathbf{s})]/2$，$Q$ 是高斯的数量，$w_i$ 是第 $i$ 个高斯的权重，而且${\phi }_{SM,i}(\mathbf{s})=\mathcal{N}(\mathbf{s};{\mu }_i,{\sum }_i)$是一个标度定位的高斯分布，其平均值为 ${\mu }_i$ ，方差为 ${\sum }_i$ 。对称化使得 ${\hat{k}}_{SM,i}(\mathbf{s})$ 成为偶函数，也就是说，对于所有 ${\hat{k}}_{SM,i}(\mathbf{s})={\hat{k}}_{SM,i}(-s)$。然后，应用傅里叶逆变换，我们可以得到如下的 SM 核：
$$\begin{array}{c}\begin{array}{rl}{k}_{SM}(\tau )& ={\mathcal{F}}_{s\to \tau }^{-1}[{\hat{k}}_{SM}(\mathbf{s})](\tau )\\ & =\sum _{i=1}^Q{\omega }_i\cos (2\pi {\tau }^T{\mu }_i)\exp (-2{\pi }^2\tau \sum _i{\tau }^T)\end{array}\end{array}\text{\hspace{1em}(4)}$$
其中 ${\mathcal{F}}_{s\to \tau }^{-1}$表示从频域到时域的反傅里叶变换算子。对于SM内核，我们可以将${\omega }_i$，${\mu }_i$和 ${\sum }_i$ 分别解释为第 $i$ 个协方差分量的信号方差，逆周期和逆长度尺度。总而言之，SM内核可以看作是现有固定内核的概括。请注意，具有SM内核的GP模型已用于无线流量预测 [34]，并且受到无线通信应用的信任。在第六节中，我们通过使用带有SM内核的GP模型来预测在线5g用户的数量。

4.2 具有非平稳内核的GP

略

4.3 可解释的深度内核

略

4.4 使用多任务内核的集体智能

略

V 可扩展的分布式高斯过程

  无线通信中的分布式高斯过程 (DGP) 涉及在分布式边缘设备上的学习。使用 DGP 可以避免与中央服务器的频繁交互，并允许每个边缘设备拥有局部学习模型。对于自动驾驶汽车和无人驾驶飞机等对延迟敏感的应用，局部学习模型可以及时快速响应局部请求。特别地，当中央服务器不可用或发生网络拥塞时，DGP可以节省无线通信的总体时间成本。因此，DGP可以看作是设备上智能的一种形式，它解决了无线通信中可伸缩计算和隐私保护的主要问题。

  在本节中，我们介绍DGP的框架，该框架在计算效率方面显示出显着优势 [1,35，106，107]。选择 DGP 的原因有很多，例如将普通 GP 扩展到大型数据集、将普通 GP 应用于分布式边缘数据集、防止访问隐私敏感数据以及充分利用多核高性能计算机 (HPC)。通常，DGP将大数据拆分为多个 ( $M$ 个) 在本地计算节点上计算的较小部分，以加快整个模型的推断 [108]，从而避免集中收集和存储海量数据。 DGP的最初目标是使GP可扩展到大数据。然而，随着物联网网络中多核计算体系结构和边缘计算的发展，DGP正逐渐受到研究和工业应用的关注，因为它提供了比现有GPs更实用的机器学习框架。最近出版了一些有代表性的DGP作品 [1,35，106-109]。通过使用 Map-Reduce 框架并解耦以诱导点为条件的数据，提出了一种针对 GP 和潜在变量模型 (LVM) 的分布式变分推理 [108]。当数据大小为 $n\ge 10^7$ 时，GP的分布式变分推理仍然具有可伸缩推理的局限性。**另一个DGP基于专家混合 (MoE) 模型 [110]。MoE模型对所有本地专家模型 (node) 的预测进行加权，以给出最终的预测。**对于 MoE 来说，困惑是如何指定专家的数量和每个专家的权重。与MoE相比，增加独立 GP 专家预测的GP专家乘积模型（PoE）[109]可以避免为专家分配权重，但不可避免地会过度自信。PoEs的边际似然 $p(\mathbf{y}|X,\Theta )$ 写为:
$$p(\mathbf{y}|X,\Theta )\approx \underset{i=1}{\overset{M}{\Pi }}{p}^{(i)}({\mathbf{y}}^{(i)}|X^{(i)},\Theta )\text{\hspace{1em}(13)}$$

其中 $M$ 是GP专家的数量，$p^{(i)}(y^{(i)}|X^{(i)}，\Theta )$ 是第 $i$ 个GP专家使用数据集 { X , y } {X, mathbf y} {X,y} 的第i个分区 { X ( i ) ， y ( i ) } {X^{(i)}，y^{(i)}} {X(i)，y(i)} 的边际可能性。此外，PoE 的预测概率是独立 GP 专家的所有预测概率的乘积，
$$p(f_{\ast }|{\mathbf{x}}_{\ast },\mathbf{y},X)\approx \underset{i=1}{\overset{M}{\Pi }}{p}^{(i)}(f_{\ast }|{\mathbf{x}}^{\ast },{\mathbf{y}}^{(i)},X^{(i)})\text{\hspace{1em}(14)}$$

  类似地，贝叶斯委员会机器 (BCM) [111] 通过使用贝叶斯规则组合在不同数据集上训练的独立估计量。由于考虑了 GP 先验 $p(f_{\ast })$，BCM 具有更好的解释。此外，强大的 BCM [112] 通过结合 GP 先验和 GP 专家的重要性，概括了原始 BCM 和 PoE-GP。为了更好地近似全GP，其他改进的DGP工作包括：(1）异步分布式变异GP[107]，使用权重空间增强，将GP扩展到数十亿的样本。(2) 广义鲁棒BCM [113]，通过随机选择子集 ${\mathcal{D}}^{(1)}$ 作为与其余子集通信的全局节点，获得一致的聚合预测分布；(3) 嵌套克里格预测器，根据观察点的子集汇总子模型[114] 。

VI 使用 GP 的数据驱动无线通信示例：在线 5G 用户的预测

略

VII 基于GP的无线应用

  在本节中，为了展示 GP 在无线通信中的广泛应用，我们将进一步回顾和讨论三个典型应用：无线流量预测、定位和轨迹规划。
略

VIII 未来无线通信的 GP

  从使用 GP 进行无线通信的动机来看，我们注意到有许多新出现的困难。我们概述了未来数据驱动无线通信的 GP 模型的一些具有挑战性的未解决问题。

• 用于密集和分散无线通信系统的超大规模分布式 GP。 在未来数据驱动的无线通信中，广泛存在的传感器随时收集大量数据，从而导致大量可观的数据传输和存储。降低数据传输和存储成本的有效且务实的解决方案是进行超大规模分布式机器学习。尽管目前 GP 的可扩展性是可用的。然而，超大规模分布式GP仍然是一个开放的研究问题。
• **用于无线通信系统中多模态数据的 GP。**目前，GP模型只能从无线通信系统生成的结构化数据中学习。还有从不同类型的传感器收集的多模态数据，例如来自智能手机的数值原始数据、来自无人机超声波传感器的超声波数据、来自监控摄像机的图像和视频以及来自语音传感器的自然语言。特别地，经由LTE/5g无线网络和核心网络的接口传输的信令和数据始终是非结构化的。因此，从无线通信系统中的非结构化和多模式数据中学习是GP模型的另一个挑战。
• 无线通信系统中具有深层结构的高解译GPS。 GP的深层内核存在困难，因为它增加了GP模型的灵活性以及模型解释的难度。从平稳核和非平稳核的定理来看，频域中深核的数学定义仍然不清楚。与DNN类似，在数据驱动的无线通信中牺牲可解释性通常是学习和理解网络之间的折衷选择，这对于高复杂性状态预测而言不太可以容忍。因此，追求具有深层结构的高度可解释的GP将是未来数据驱动的无线通信中的关键问题。
• 增强隐私的GP，以解决隐私问题和法律问题。 由于机器学习模型依赖于所需训练和预测数据的共享，因此必须解决潜在的隐私泄露问题。一种隐私增强GP解决方案是完全或部分同态加密（HE）[124]，另一种隐私增强GP解决方案采用差分隐私（DP）技术[125]。然而，HE 技术可能会引入大量计算开销，而 DP 技术可能会降低训练过程的性​​能。此外，一种新兴的隐私增强技术是通过利用联邦学习 [126, 127] 来协作学习共享模型，同时将所有训练数据保存在本地设备上。然而，为无线通信设计有效的隐私保护联邦学习的 GP 仍然是一个开放的挑战。

IX 结论

  在本文中，我们从动机，GP模型的定义和构建，使用不同内核的GP表现力以及分布式GP可伸缩性方面全面回顾了使用GPs的数据驱动无线通信。具有贝叶斯性质的 GP 可以通过指定协方差函数对一大类无线通信系统进行建模。通过使用分布式方法，GP 模型能够对无线网络中的大数据执行可扩展的推理。使用 GP 的数据驱动无线通信系统可以实现所需的属性、表现力、可扩展性、可解释性和不确定性建模。由于收集到的丰富数据和无线网络中的建模复杂性，这些特征对于无线通信中的模型变得至关重要。特别是，由于其数学定义，可解释性和不确定性建模是 GP 的固有优势。从 GP 模型在无线通信中的现有应用来看，我们提出 GP 模型可以很好地涵盖上述数据驱动的无线通信的特性，这已被成功证明是有价值的。

最后

以上就是俏皮山水为你收集整理的论文阅读5 | Recent Advances in Data-Driven Wireless Communication Using Gaussian Processes: A Comprehens摘要I 简介II 数据驱动的无线通信: 具有独特功能的动机III 用于机器学习的高斯过程的背景IV GP内核的进展V 可扩展的分布式高斯过程VI 使用 GP 的数据驱动无线通信示例：在线 5G 用户的预测VII 基于GP的无线应用VIII 未来无线通信的 GPIX 结论的全部内容，希望文章能够帮你解决论文阅读5 | Recent Advances in Data-Driven Wireless Communication Using Gaussian Processes: A Comprehens摘要I 简介II 数据驱动的无线通信: 具有独特功能的动机III 用于机器学习的高斯过程的背景IV GP内核的进展V 可扩展的分布式高斯过程VI 使用 GP 的数据驱动无线通信示例：在线 5G 用户的预测VII 基于GP的无线应用VIII 未来无线通信的 GPIX 结论所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。