matlab延迟传函,[MATLAB使用练习] [教材：自动控制原理-裴润] 2.5 MATLAB用于处理系统数学模型...

MATLAB程序设计语言是一种高性能的数值计算软件。经过十几年的发展，MATLAB已经成为适合多学科，功能齐全的大型科学计算软件。目前MATLAB已经成为线性代数、自动控制理论、数理统计和数字信号处理分析、动态系统仿真等课程的基本数学工具。它的TOOLBOX工具箱与SIMUINK仿真工具，为控制系统的计算与仿真提供了一个强有力的工具，使控制系统的计算与仿真的传统方法发生了革命性的变化。MATLAB已经成为国际控制领域最流行的计算与仿真软件。

2.5.1 拉氏变换与拉氏反变换

求拉氏变换可用函数   laplace(ft,t,s)

例2.5.1 求

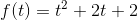 的拉氏变换

解 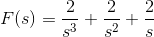 程序运行如下：

>> syms s t;

>> ft = t^2+2*t+2;

>> FS = laplace(ft,t,s)

FS =

(2*(s + 1))/s^2 + 2/s^3

其中 syms 是符号变量设置函数，其使用的格式为 syms arg1 arg2 ...;

求拉氏反变换可用函数 ilaplace(Fs,s,t)

例 2.5.2 求 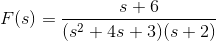 的拉式反变换

解 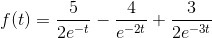    程序运行如下：

>> syms s t

>> Fs = (s+6)/((s^2+4*s+3)*(s+2));

>> ft = ilaplace(Fs,s,t)

ft =

(5*exp(-t))/2 - 4*exp(-2*t) + (3*exp(-3*t))/2

2.5.2 多项式运算

在MATLAB中采用行向量表示多项式，行向量内的各元素是按降幂次排列的多项式系数。

多项式

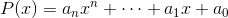 的系数行向量为 

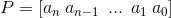
求多项式的根可以用 roots(p)函数

例 2.5.3 求多项式

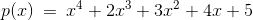的根

程序运行如下：

>> P = [1 2 3 4 5];

>> r = roots(P)

r =

-1.2878 + 0.8579i

-1.2878 - 0.8579i

0.2878 + 1.4161i

0.2878 - 1.4161i

由已知多项式的根求多项式可用函数 poly(r)

例2.5.4 已知多项式的根分别为 -1，-5，-8，试求对应的多项式

所求多项式为

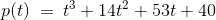 , 可进一步用 roots(p) 函数来验证结果，程序运行如下：

>> PL = poly([-1 -5 -8])

PL =

1 14 53 40

>> roots(PL)

ans =

-8.0000

-5.0000

-1.0000

2.5.3 微分方程求解

求解微分方程可采用指令 s=dslove('a_1'，'a_2'， …，‘a_n’). 其中，输入变量包括三部分内容:微分方程、初始条件、指定的独立变量。其中微分方程必不可少，其余内容看情况给。默认的独立变量是 ‘t’ ，也可用别的变量代替 ‘t’，把它放在输入变量最后即可。字母 ‘D’ 代表微分算子，即

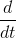 ，字母‘D’ 后面的数字表示微分的阶次，如 D2 代表  

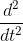，微分算子后的字母代表被微分的变量，如 D3y 代表 y(t) 的三阶微分。初始条件可按如下形式给出：‘y(a) = b’ 或 'Dy(a) = b'. 若初始条件未给定，则结果含积分常数 C1.

例 2.5.5 解微分方程 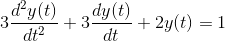   ，初始条件  

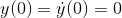
解 程序运行如下：

>> y = dsolve('3*D2y + 3*Dy + 2*y = 1','y(0)=0','Dy(0)=0')

y =

1/2 - (15^(1/2)*exp(-t/2)*sin((15^(1/2)*t)/6))/10 - (exp(-t/2)*cos((15^(1/2)*t)/6))/2

2.5.4 传递函数及形式转换的建立

传递函数两种常用的表达形式是有理分式形式和零极点形式。

有理分式形式的一般表达式为

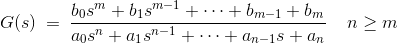
零极点形式的一般表达式为

    ，

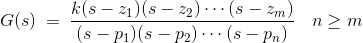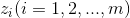  传递函数的零点；

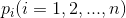   传递函数的极点；

k 零极点形式传递函数的系数。

建立有理分式形式的传递函数时，需先将传递函数分子、分母多项式的系数写成两个行向量，然后用tf()函数给出，格式为

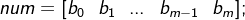
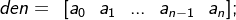
g = tf(num , den)

将传函从 有理形式 转换为 零极点形式，可用函数 zpk(g).

例 2.5.6 在MATLAB中表示多项式形式的传函 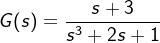  ，并将其转换为零极点形式

解 程序运行如下：

>> num =[1 3];

>> den = [1 0 2 1];

>> g = tf(num , den)

g =

s + 3

-------------

s^3 + 2 s + 1

Continuous-time transfer function.

>> zpk(g)

ans =

(s+3)

----------------------------------

(s+0.4534) (s^2 - 0.4534s + 2.206)

Continuous-time zero/pole/gain model.

若要建立零极点形式的传函可使用函数 zpk()，这时要结果传函的零点、极点 分别写成两个向量，给出传函的增益，格式为

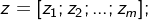
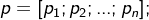
k = 增益值

g = zpk(z,p,k)

若想将传函由  零极点形式 转换为 多项式形式，可用函数 tf()，格式为 tf(g)

例 2.5.7 在MATLAB中表示零极点形式的传函 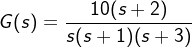，并将其转换成 多项式形式的传函

解 程序运行如下：

>> z = [-2];

>> p = [0 -1 -3];

>> k = 10;

>> g = zpk(z,p,k)

g =

10 (s+2)

-------------

s (s+1) (s+3)

Continuous-time zero/pole/gain model.

>> tf(g)

ans =

10 s + 20

-----------------

s^3 + 4 s^2 + 3 s

Continuous-time transfer function.

注意：稳定系统的极点都有负实部。若有复数的零极点，则应有共轭的零极点同时输入。输入虚部时， j 或 i 是MATLAB中约定的虚数单位符号，应与系数用 “ * ” 相乘，若传函无零点，则用 z = [ ]输入空向量。

例 2.5.8 传函极点为

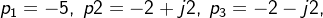 没有零点，增益为100，试建立零极点形式及多项式形式的传函。

解 程序运行如下：

>> z =[];

>> p = [-5 -2+j*2 -2-j*2];

>> k=100;

>> g = zpk(z,p,k)

g =

100

--------------------

(s+5) (s^2 + 4s + 8)

Continuous-time zero/pole/gain model.

>> tf(g)

ans =

100

-----------------------

s^3 + 9 s^2 + 28 s + 40

Continuous-time transfer function.

传函有纯时间延迟环节

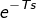，建立传函时 延迟时间赋给 变量dt，使用 tf() 函数时还要用 ‘inputdelay’说明。

例 2.5.9 已知系统传函为 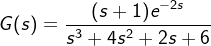 ，在MATLAB中建立传函。

解  程序运行如下：

>> num = [1 1];

>> den = [1 4 2 6];

>> dt = 2;

>> g = tf(num,den,'inputdelay',dt)

g =

s + 1

exp(-2*s) * ---------------------

s^3 + 4 s^2 + 2 s + 6

Continuous-time transfer function.

>> zpk(g)

ans =

(s+1)

exp(-2*s) * ---------------------------------

(s+3.883) (s^2 + 0.1171s + 1.545)

Continuous-time zero/pole/gain model.

2.5.5 部分分式展开

控制系统中的传函是 s 有理分式

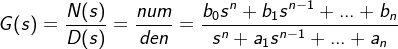      N(s)，D(s) 为传函的分子(母)多项式。

MATLAB中分别用行向量 num ， den 表示其系数，即：

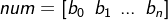
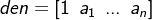
命令     [r,p,k] = residue(num,den)  可求出传函 部分分式展开式 的留数、极点、余项

部分分式展开式 如下：

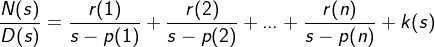，其中

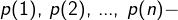 极点；

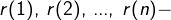 部分分式展开式的留数；

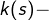 余项。

例 2.5.10 系统传函 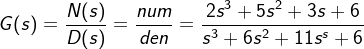 ， 试展开为部分分式。

解 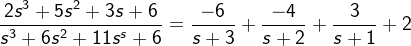        ，  程序运行如下：

>> num = [2 5 3 6];

>> den = [1 6 11 6];

>> [r p k] = residue(num,den)

r =

-6.0000

-4.0000

3.0000

p =

-3.0000

-2.0000

-1.0000

k =

2

例 2.5.11 系统传函为 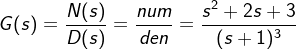  ， 将其展开成部分分式形式。

解 先将分母展开成降幂形式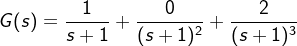，     ， 程序运行如下：

>> num = [1 2 3];

>> den = [1 3 3 1];

>> [r p k] = residue(num,den)

r =

1.0000

0.0000

2.0000

p =

-1.0000

-1.0000

-1.0000

k =

[]

2.5.6 串联、并联、反馈结构的化简

1.串联结构的化简

series()函数

例 2.5.12两个环节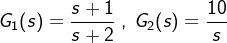  串联，求等效传函 G(s).

解 程序运行如下，函数 printsys(num,den) 用于打印传函

>> num1 = [1 1];

>> den1 = [1 2];

>> num2 = [10];

>> den2 = [1 0];

>> [num,den] = series(num1,den1,num2,den2)

num =

0 10 10

den =

1 2 0

>> printsys(num,den)

num/den =

10 s + 10

---------

s^2 + 2 s

2.并联结构的化简

Parallel()函数

例 2.5.13 两环节并联，其中 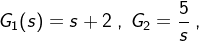  求等效传函G(s)。

解 程序运行如下：

>> num1 = [1 2];

>> den1 = [0 1];

>> num2 = [0 5];

>> den2 = [1 0];

>> [num den] = parallel(num1,den1,num2,den2)

num =

1 2 5

den =

0 1 0

>> printsys(num,den)

num/den =

s^2 + 2 s + 5

-------------

s

3.反馈结构的化简

前向通道传函 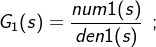 反馈通道传函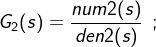 

等效闭环传函

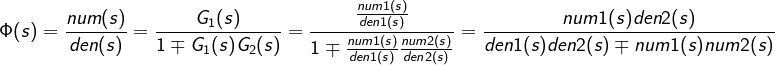
函数feedback(sys1,sys2,sign)可用来化简反馈结构，参数sign表示反馈量在相加点的符号，默认为负反馈。

例 2.5.14 反馈结构中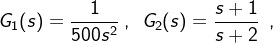，  相加点处符号为负(负反馈)，求等效闭环传函。

解 程序运行如下：

>> num1 = [1];

>> den1 = [500 0 0];

>> num2 = [1 1];

>> den2 = [1 2];

>> [num den] = feedback(num1,den1,num2,den2)

num =

0 0 1 2

den =

500 1000 1 1

>> printsys(num,den)

num/den =

s + 2

---------------------------

500 s^3 + 1000 s^2 + s + 1

第二章仿真练习先做到这里~

^_^//