matlab中ode15s函数的用法,求解刚性微分方程和 DAE - 变阶方法

ode15s 求解器是适用于大多数刚性问题的首选求解器。但是，对于特定类型的问题，其他刚性求解器可能更高效。本示例使用所有四个刚性 ODE 求解器解算刚性测试方程。

请考虑以下测试方程：

y′=-λy.

随着 λ 的量级增加，方程的刚性逐渐增强。使用 λ=1×109、初始条件 y(0)=1 和时间区间 [0 0.5]。这些值使该问题足够刚性，从而使 ode45 和 ode23 需要对该方程进行积分。此外，还使用 odeset 传入常量 Jacobian J=∂f∂y=-λ 并打开求解器统计信息的显示。

lambda = 1e9;

y0 = 1;

tspan = [0 0.5];

opts = odeset('Jacobian',-lambda,'Stats','on');

使用 ode15s、ode23s、ode23t 和 ode23tb 对方程求解。生成子图进行比较。

subplot(2,2,1)

tic, ode15s(@(t,y) -lambda*y, tspan, y0, opts), toc

104 successful steps

1 failed attempts

212 function evaluations

0 partial derivatives

21 LU decompositions

210 solutions of linear systems

Elapsed time is 2.504340 seconds.

title('ode15s')

subplot(2,2,2)

tic, ode23s(@(t,y) -lambda*y, tspan, y0, opts), toc

63 successful steps

0 failed attempts

191 function evaluations

0 partial derivatives

63 LU decompositions

189 solutions of linear systems

Elapsed time is 0.350204 seconds.

title('ode23s')

subplot(2,2,3)

tic, ode23t(@(t,y) -lambda*y, tspan, y0, opts), toc

95 successful steps

0 failed attempts

125 function evaluations

0 partial derivatives

28 LU decompositions

123 solutions of linear systems

Elapsed time is 0.591374 seconds.

title('ode23t')

subplot(2,2,4)

tic, ode23tb(@(t,y) -lambda*y, tspan, y0, opts), toc

71 successful steps

0 failed attempts

167 function evaluations

0 partial derivatives

23 LU decompositions

236 solutions of linear systems

Elapsed time is 0.573255 seconds.

title('ode23tb')

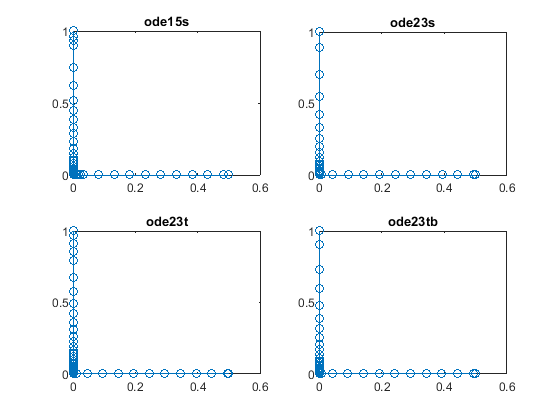
这些刚性求解器都表现不错，但对于这个特定问题，ode23s 完成积分所用的步长最少，运行速度最快。由于指定了常量 Jacobian，任何求解器都不需要计算偏导数即可计算出解。指定 Jacobian 对 ode23s 最有利，因为它通常需要在每个步长中计算 Jacobian。

对于一般的刚性问题，刚性求解器的性能因问题的形式和指定的选项而异。提供 Jacobian 矩阵或稀疏模式始终可以提高求解器解决刚性问题的效率。但是，由于刚性求解器使用 Jacobian 的方式不同，计算效率的提高程度也有很大差异。实际上，如果方程组非常大，或者要解算很多次，则非常值得研究一下不同求解器的性能，以最大程度地缩短执行时间。