(一)利用RSA进行加密
1.原理
该算法的数学基础是初等数学论中的Euler定理,其安全性建立在大整数因式分解的困难性之上,利用了单向陷门函数(如图)的原理。
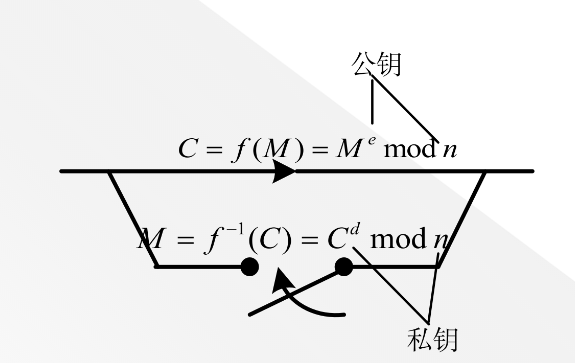
2.算法描述
明文空间P=密文空间C=Zn
密钥的生成 选择互异素数p,q,
计算 n = p ∗ q , ∅ ( n ) = ( p − 1 ) ( q − 1 ) n=p*q, emptyset(n)=(p-1)(q-1) n=p∗q,∅(n)=(p−1)(q−1)
选择整数e使 g c d ( ∅ ( n ) , e ) = 1 , 1 < e < ∅ ( n ) gcd( emptyset(n),e)=1,1<e<emptyset(n) gcd(∅(n),e)=1,1<e<∅(n)
计算d,使 d = e − 1 m o d ∅ ( n ) d=e^{-1}mod emptyset(n) d=e−1mod∅(n)
公钥Pk={e,n}
私钥Sk={d,n}
加密 (用e,n)
明文:M<n 密文: C = M e ( m o d n ) C=M^e(mod n) C=Me(modn)
解密 (用d,n)
密文:C 明文: M = C d ( m o d n ) M=C^d(mod n) M=Cd(modn)
3.安全性要求
①p与q必为足够大的素数,使 分析者没有办法在有效时间内将n分解出来。建议选择 p和q大约是100位的十进制素数。模数n的长度要求至少是 512比特。
②为了抵抗现有的整数分解算法,对RSA模n的素因子 p和q还有如下要求:
(1)|p-q|很大,通常 p和q的长度相同;
(2)p-1 和q-1分别含有大素因子p1和q1
(3)gcd(p1-1,q1-1)应该很小。
③为了提高加密速度,通常取e为特定的小整数,如EDI国际标准中规定$ e=2^{16}+1$,ISO/IEC9796中甚至允许取e=3。这时加密速度一般比解密速度快10倍以上。
4.算法总结
(1)选择两个大素数p和q,通常要求每个均大于10100。
计算n=pq和z=(p-1)(q-1)。
选择一与z互质的数、令其为d 。
找到一个e满足e×d=1 (mod z)。
(2)选好这些参数后,将明文划分成块,使得每个明文报文P 长度m满足0<m<n加密P时,计算 C = P e ( m o d n ) C=P^e(mod n) C=Pe(modn),解密C时计算 P = C d ( m o d n ) P=C^d(mod n) P=Cd(modn)。由于模运算的对称性,可以证明, 在确定的范围内,加密和解密函数是互逆的。
(3)为实现加密,需要公开(e, n),为实现解密需要(d, n)。
5.算法图

其中在解密中,欧拉定理的推理,参照:《应用密码学》/胡向东,魏琴芳,胡蓉编著. —4版. —北京:电子工业出版社,2019.6 :68
(二)利用RSA进行数字签名
签名是用自己的私钥对要签名的内容进行签名,需要进行验证的一方利用签名方的公钥进行验证

(三)加密与签名的c++源代码
注意
1.代码是写在一个头文件当中的,对RSA的加密测试,签名测试,需要在mian()里面调用
2.包含素性检测的头文件"Miller-Rabin.h",参考:素性检测(Miller-Rabin)_remandancy.h的博客-CSDN博客_素性检测
3.包欧几里得算法的头文件"Euclid.h",参考: 欧几里得函数与扩展欧几里得函数_remandancy.h的博客-CSDN博客_欧几里得函数
4.需要安装大整数集vcpkg,请参考:windows通过vcpkg安装gmp库_Fretory的博客-CSDN博客_vcpkg安装gmp,注意在安装的根目录,名录名称不要有空格
5.一份别人使用GMP写RSA的参考:基于GMP大数库用 “ 快速幂取模算法 ” + “ 扩展欧几里得算法 ”实现RSA加密算法(C++实现)_Em0s_Er1t的博客-CSDN博客
#pragma once
#include<gmp.h>
#include<gmpxx.h>
#include<iostream>
#include<vector>
#include"Miller-Rabin.h"
#include"Euclid.h"
using namespace std;
class RSA
{
public:
RSA();
~RSA();
//void Init(int len);//初始化密钥,公钥,输入为密钥的长度(素数的长度)
void Init(mp_bitcnt_t len);
void SetMeesge();//设置明文
void SetCipher();//设置密文
void Encryption();//加密
void Decryption();//解密
void Signature();//签名
void Authenticate();//认证
private:
mpz_class p, q,d;//两个大素数,私钥d
mpz_class n, e;//公钥
mpz_class eurl;//欧拉数(p-1)(q-1)
mpz_class *message, *cipher,*temp;
int textsize = 0;
int cipsize = 0;
};
RSA::RSA()
{
}
RSA::~RSA()
{
}
//inline void RSA::Init(int len)//初始化密钥,公钥,输入为密钥的生成0-len长度的密钥
//{
// //产生随机数的范围
// mpz_class temp1=1, temp2=1,subtemp=0;
// for (int i =1; i < len; i++)
// {
//
temp1 = temp1 * 10;
// }
// temp2 = temp1 * 10;
// subtemp = temp2 - temp1;
// //产生随机数
// mpz_class ran;
// gmp_randclass rr(gmp_randinit_default);//设置随机数生成算法为默认
// rr.seed(time(NULL));//设置随机化种子为当前时间;
// while (1)
// {
//
ran = rr.get_z_bits(512);//生成125bit的随机数
//
mpz_class random = ran.get_ui(); //生成随机数
//
p = random % subtemp + temp1;//生成temp1-temp2之间的随机给p
//
if (Miller_Rabin(p))
//
{
//
break;
//
}
// }
// cout << "p=" << p << endl;
// while (1)
// {
//
ran = rr.get_z_bits(512);//生成512bit的随机数
//
mpz_class random = ran.get_ui(); //生成随机数
//
q = random % subtemp + temp1;//生成temp1-temp2之间的随机数给q
//
if (Miller_Rabin(q)&&(q!=p))
//
{
//
break;
//
}
// }
// cout << "q=" << q << endl;
// n = p * q;
// cout << "n=" << n << endl;
// eurl = (p - 1)*(q - 1);
// cout << "eurl=" << eurl << endl;
// while (1)
// {
//
ran = rr.get_z_bits(512);//生成512bit的随机数
//
mpz_class random = ran.get_ui(); //生成随机数
//
e = random % (eurl - 1)+1;//生成1-euil之间的数
//
if (GCD(e, eurl) == 1)//判断是否互素
//
{
//
break;
//
}
// }
// cout << "e=" << e << endl;
// d = ExtendedEuclid(e, eurl);
// d = d + eurl;
// cout << "d=" << d << endl;
//}
inline void RSA::Init(mp_bitcnt_t len)//初始化密钥,公钥,输入为密钥的生成0-len长度(bit)的密钥
{
//产生随机数的范围
//产生随机数
mpz_class ran;
gmp_randclass rr(gmp_randinit_default);//设置随机数生成算法为默认
rr.seed(time(NULL));//设置随机化种子为当前时间;
while (1)
{
ran = rr.get_z_bits(len);//生成lenbit的随机数
p = ran.get_ui(); //生成随机数
if (Miller_Rabin(p))
{
break;
}
}
cout << "p=" << p << endl;
while (1)
{
ran = rr.get_z_bits(len);//生成512bit的随机数
q = ran.get_ui(); //生成随机数
if (Miller_Rabin(q)&&(q!=p))
{
break;
}
}
cout << "q=" << q << endl;
n = p * q;
cout << "n=" << n << endl;
eurl = (p - 1)*(q - 1);
cout << "eurl=" << eurl << endl;
e = 5;
//while (1)
//{
// ran = rr.get_z_bits(len);//生成512bit的随机数
// mpz_class random = ran.get_ui(); //生成随机数
// e = random % (eurl - 1)+1;//生成1-euil之间的数
// if (GCD(e, eurl) == 1)//判断是否互素
// {
//
break;
// }
//}
cout << "e=" << e << endl;
d = ExtendedEuclid(e, eurl);
d = d + eurl;
cout << "d=" << d << endl;
}
inline void RSA::SetMeesge()
{
cout << "请输入明文:";
string text;
cin >>text;
textsize = text.size();
message = new mpz_class[textsize];
for (int i = 0; i < textsize; i++)
{
message[i] = (int)text[i];
}
}
inline void RSA::SetCipher()
{
cout << "对密文进行解密:";
cipher = temp;
}
inline void RSA::Encryption()
{
/*cout << "请输入明文:";
string text;
cin >> text;
textsize = text.size();
message = new mpz_class[textsize];
for (int i = 0; i < textsize; i++)
{
message[i] = (int)text[i];
}*/
cout << "加密结果:";
temp = new mpz_class[textsize];
for (int i = 0; i < textsize; i++)
{
temp[i] = Quick_Power_Mod(message[i], e, n);
cout << temp[i]<<",";
}
}
inline void RSA::Decryption()
{
cout << "解密结果:";
for (int i = 0; i < textsize; i++)
{
temp[i] = Quick_Power_Mod(temp[i], d, n);
cout << (char)(temp[i].get_ui());
}
}
void RSA::Signature()
{
cout << "输出需要签名的内容:";
string text;
cin >> text;
textsize = text.size();
message = new mpz_class[textsize];
for (int i = 0; i < textsize; i++)
{
message[i] = (int)text[i];
}
//签名:
temp = new mpz_class[textsize];
for (int i = 0; i < textsize; i++)
{
temp[i] = Quick_Power_Mod(message[i], d, n);
cout << temp[i] << ",";
}
}
void RSA::Authenticate()
{
cout << endl<<"认证结果:";
for (int i = 0; i < textsize; i++)
{
temp[i] = Quick_Power_Mod(temp[i], e, n);
cout << (char)(temp[i].get_ui());
}
}
void RSATest()//加密解密
{
RSA rsa;
int len;
cout << "素数长度(bit):";
cin >> len;
rsa.Init(len);
rsa.SetMeesge();
rsa.Encryption();
cout << endl;
rsa.SetCipher();
rsa.Decryption();
}
void RSASinAndAuth()//签名与认证
{
RSA rsa;
int len;
cout << "素数长度(bit):";
cin >> len;
rsa.Init(len);
rsa.Signature();
rsa.Authenticate();
}
运行结果
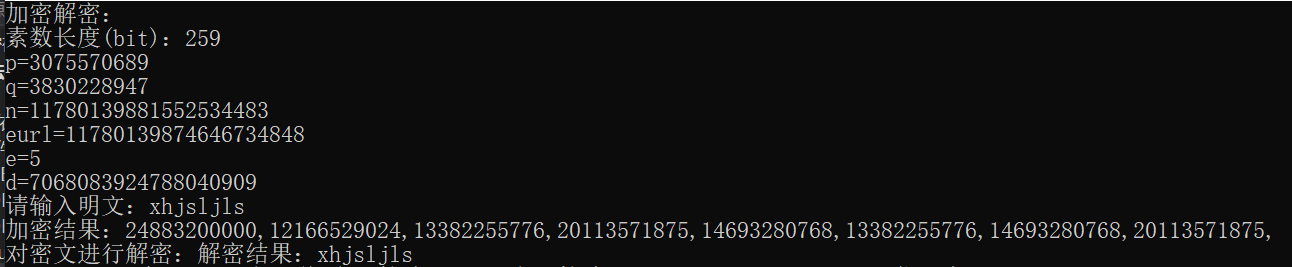

最后
以上就是帅气夕阳最近收集整理的关于RSA利用大整数实现加密解密与签名认证的全部内容,更多相关RSA利用大整数实现加密解密与签名认证内容请搜索靠谱客的其他文章。








发表评论 取消回复