一、MATLAB基本功能
1、MATLAB帮助
(1)help函数
help可用于查看对应函数的帮助文本
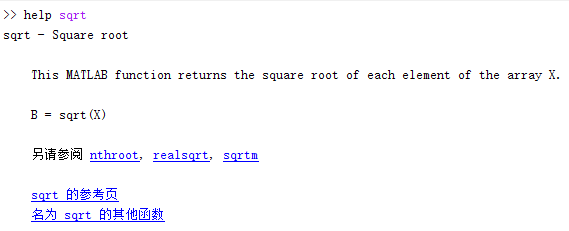
(2)lookfor函数
如果不知道具体的函数名,单知道函数相关的某个关键字,则可以使用lookfor进行查找。

(3)常见帮助命令
| help:获取帮助 | helpwin:运行帮助窗口 |
| who:列出当前工作空间中的变量 | whos:列出当前工作空间变量的更多信息 |
| what:列出当前文件夹或指定目录下的M文件、MAT文件、MEX文件 | which:显示指定函数或文件的路径 |
| exist:检查指定变量或文件的存在性 |
2、简单实例
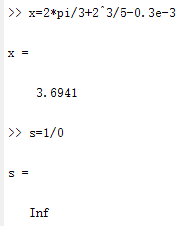
预定义变量
| 变量 | 说明 |
| eps | 计算机的最小正数 |
| pi | 圆周率 |
| inf或Inf | 无穷大 |
| NaN | 不定量 |
| i,j | 虚数单位定义i |
| flops | 浮点运算次数统计计算量 |

3、MATLAB界面
(1)MATLAB搜索路径
通过选择MATLAB主窗口的设置路径,进入“设置路径”对话框,可为MATLAB添加或删除搜索路径。
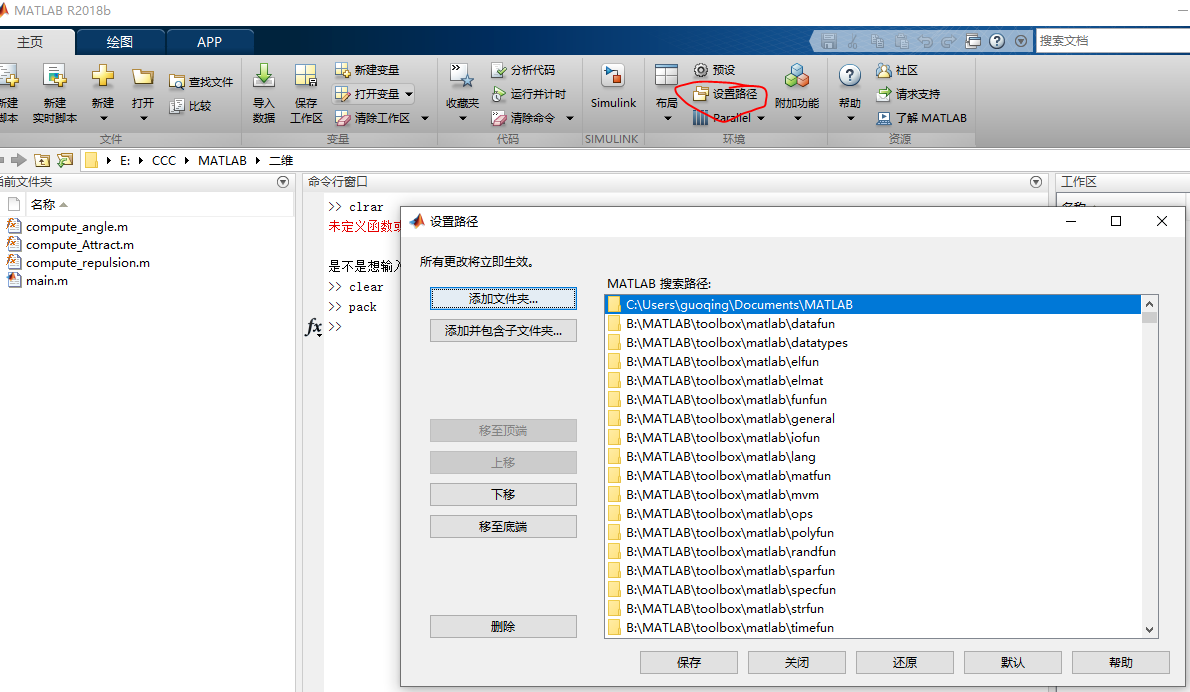
MATLAB通过设置路径来获取存储在硬盘上的文件信息。
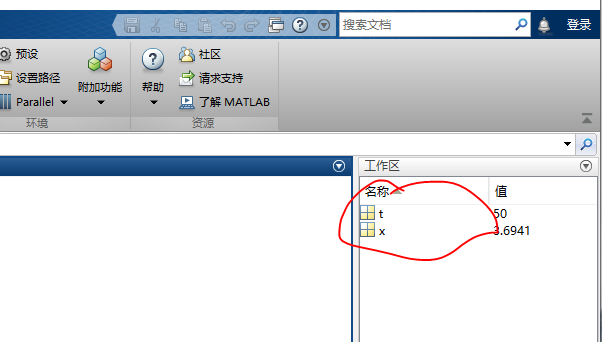
(2)工作区浏览器
MATLAB桌面左上角工作空间窗口允许用户改变工作区内容的如何一个变量的内容。
4、MATLAB基本功能
(1)命令行窗口
| 命令 | 命令说明 | 命令 | 命令说明 |
| cd | 显示或改变当前文件夹 | load | 加载指定文件的变量 |
| dir | 显示当前文件夹或指定文件夹的文件 | diary | 日志文件命令 |
| clc | 清楚工作窗中的所有显示内容 | ! | 调用DOS命令 |
| home | 将光标移至命令行窗口的最左上角 | exit | 退出MATLAB |
| clf | 清楚图形窗口 | quit | 退出MATLAB |
| type | 显示文件内容 | pack | 收集内存碎片 |
| clear | 清楚内存变量 | hold | 图形保持开关 |
| echo | 工作窗信息显示开关 | path | 显示搜索目录 |
| disp | 显示变量或文字内容 | save | 保存内存变量到指定文件 |
(2)计算器功能
| 运算 | 符号 | 运算 | 符号 |
| 加法 | + | 除法 | /或 |
| 减法 | - | 乘方 | ^ |
| 乘法 | * |
多数情况下,输入行中的空格不会对MATLAB运算产生影响。另外,在MATLAB中乘法的优先级高于加法。若没有指定输出结果名称,MATLAB将默认的运算结果命名为ans。
(3)简单矩阵的输入
MATLAB中,不必对矩阵维数做如何说明,存储将自动配置。直接输入矩阵时,矩阵元素用空格或逗号分隔,矩阵行用“;”隔离。整个矩阵放在"[ ]"中。

矩阵还可以分行输入

矩阵元素输入
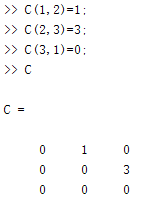
常用标点
| 名称 | 标点 | 作用 |
| 逗号 | , | 用作要显示计算结果的指令与其后指令之间的分隔; 用作输入量与输入量之间的分隔; 用作数组元素分隔符号 |
| 黑点 | . | 数组表示中,用作小数点; 用于运算符号前,构成“数组”运算符 |
| 分号 | ; | 用于指令的结尾,抑制计算结果的显示; 用作不显示计算结果指令与其后指令的分隔; 用作数组的行间分隔符 |
| 冒号 | : | 用于生成一位数组; 用作单下标援引时,表示全部元素构成的长列; 用作多下标援引时,表示那维上的全部元素 |
| 注释号 | % | 有它启首的所有物理行部分被看作非执行的注释 |
| 单引号 | ' ' | 字符串记述符 |
| 圆括号 | ( ) | 改变运算次序; 在数组援引时用; 函数指令输入宗量列表时用 |
| 方括号 | [ ] | 输入数组时用; 函数指令输入宗量列表时用 |
| 花括号 | { } | 胞元数组记述符; 图形中被控特殊字符括号 |
| 下连符 | - | 用作一个变量、函数文件名中的连字符; 图形中被控下脚标前导符 |
| 续航号 | ... | 由三个以上连续黑点构成。它把其下的物理行看作该行的逻辑继续 |
| @ | @ | 放在函数名前,形成函数句柄; 匿名函数前导符; 放在目录前,形成用户对象类目录 |
| 空格 | 用作输入量与输入朗之间的分隔符; 数组元素分隔符 |
(4)复数类型
复数的一般形式 C=a+bi,可以用赋值语句或函数complex来产生复数
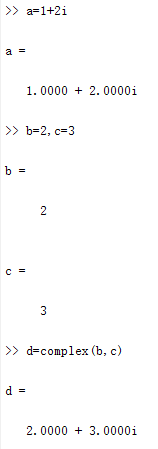
| 函数 | 描述 |
| conj(c) | 计算c的共轭复数 |
| real(c) | 返回复数c的实部 |
| imag(c) | 返回复数c的虚部 |
| isreal(c) | 如果数组c中没有一个元素有虚部,函数isreal将返回1 |
| abs(c) | 返回复数c模 |
| angle(c) | 返回数c的幅角 |
(5)初等函数运算
| 函数名 | 功能描述 | 函数名 | 功能描述 |
| sin | 正弦 | sec | 正割 |
| sind | 正弦,输入以度为单位 | secd | 正割,输入以度为单位 |
| sinh | 双曲正选 | sech | 双曲正割 |
| asin | 反正弦 | asec | 反正割 |
| asind | 反正弦,输出以度为单位 | asced | 反正割,输出以度为单位 |
| asinh | 反双曲正弦 | asech | 反双曲正割 |
| cos | 余弦 | csc | 余割 |
| cosd | 余弦,输入以度为单位 | cscd | 余割,输入以度为单位 |
| cosh | 双曲余弦 | csch | 双曲余割 |
| acos | 反余弦 | acsc | 反余割 |
| acosd | 反余弦,输出以度为单位 | acscd | 反余割,输出以度为单位 |
| acosh | 反双曲余弦 | acsch | 反双曲余割 |
| tan | 正切 | cot | 余切 |
| tand | 正切,输入以度为单位 | cotd | 余切,输入以度为单位 |
| tanh | 双曲正切 | coth | 双曲余切 |
| atan | 反正切 | acot | 反余切 |
| atand | 反正切,输出以度为单位 | acotd | 反余切,输出以度为单位 |
| atan2 | 四象限反正切 | acoth | 反双曲余切 |
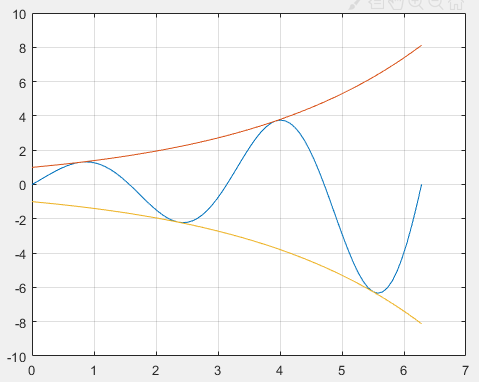
如,计算0~2的正弦函数,余弦函数
>> x=0:pi/10:2*pi;
>> y1=sin(x);
>> y2=cos(x);
>> figure(1);
>> help figure
>> plot(x,y1,'b-',x,y2,'ro-');
>> xlabel('X取值');
>> ylabel('函数值');
>> legend('正弦函数','余弦函数'); 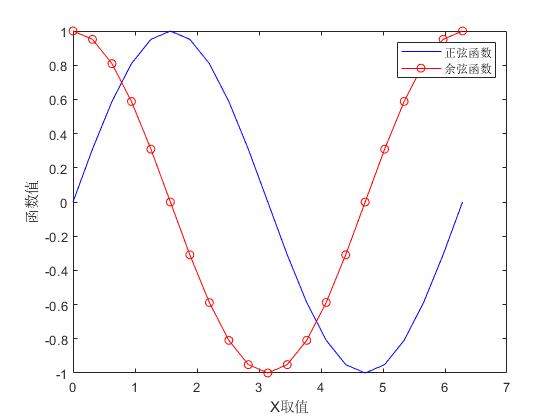
(6)指数和对数函数
| 函数名 | 功能描述 | 函数名 | 功能描述 |
| exp | 指数 | realpow | 对数,若结果是复数则报错 |
| expm1 | 准确计算exp(x)-1的值 | realog | 自然对数,若输入不是正数则报错 |
| log | 自然对数以e为底 | realsqrt | 开平方根,若输入不是正数则报错 |
| log1p | 准确计算log(1+x)的值
| sqrt | 开平方根 |
| log10 | 常用对数(以10为底) | nthroot | 求x的n次平方根 |
| log2 | 以2为底的对数 | nextpow2 | 返回满足2^p>=abs(N)的最小正整数P,其中N为输入
|
二、关系和逻辑运算
1、关系运算符
| 关系运算符 | 描述 | 关系运算符 | 描述 |
| < | 小于 | >= | 大于等于 |
| <= | 小于等于 | == | 等于(非赋值) |
| > | 大于 | ~= | 不等于 |

等于运算符(==):如果两个变量值相同将会返回变量值1,如果不同将会返回0;
不等运算符(~=):如果两个变量值不同则返回1,相同则返回0.
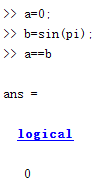
理论上a和b应该相等,但由于为近似值,故产生了round off错误,可以检测两数之间在一定的范围内是否近似相等

2、逻辑运算符
| 逻辑运算符 | 描述 |
| & | 在两个逻辑数组之间逐元素的与操作 |
| | | 在两个逻辑数组之间逐元素的或操作 |
| ~ | 对一个逻辑数组进行取反操作 |
| xor(x,y) | 逻辑异或操作,当x和y一个为0,一个不为0返回true,同时为0或为1,返回false |
| any(x) | 如x为向量,当x的任意一个元素不为0时返回true,否则返回false;如果x是数组,对于x的每一列,如果有一个元素不为0,则返回true,否则返回false |
| all(x) | 如果x都不为0时返回true,否则返回false |
三、简单数组
1、一维数组的创建
(1)直接输入:
行向量

列向量

(2)用":"生产向量
a=j:k生产的向量是a[j,j+1,..,k]
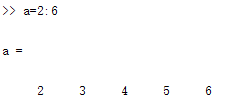
a=j:d:k生成行向量a=[j,j+d,...,j+m*d],其中m=fix((k-j)/d)
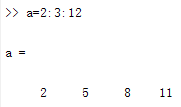
(3)函数inspace生成按等差形式排列的行向量
在X1和X2之间默认生成100个线性分布的数据,相邻两个数据的差保持不变,构成等差数列。
x=linspace(X1,X2)
x=(X1,X2,n)
在x1和x2之间生成n个线性分布的数据。相邻两个数据的差保持不变同样能构成等差数列。
2、行向量转置为列向量
(1)直接转置(')

(2)使用transpose函数

3、二维数组的创建
二维数组由实数或复数排列成矩形构成,从数据结构上看,矩阵和二维数组没有区别。
直接输入
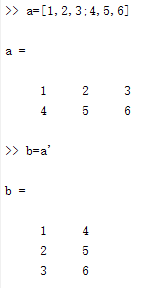

4、数组寻址
(1)对一位数组进行寻址
下标写成一个数或者一个数组即可以进行访问
对一维数组的其中一个元素进行访问

对一维数组的多个元素进行访问
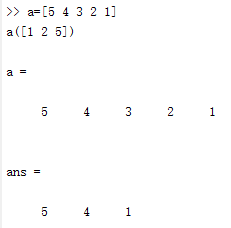
还可以使用另一种方法实现上诉功能

(2)对二维数组进行寻址
二维数组寻址与一维数组寻址一样,只不过需要考虑二维数组的行和列,二一维数组只需要考虑一个行或列,所以对二维数组有以下三种方法。
全下标法:指定行、列访问
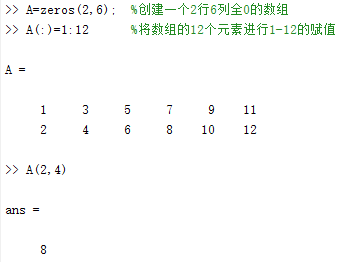
单下标法:单下标法进行访问,数组顺序为先列后行

最后
以上就是现代白羊最近收集整理的关于MATLAB工程仿真基础的全部内容,更多相关MATLAB工程仿真基础内容请搜索靠谱客的其他文章。








发表评论 取消回复