目标跟踪之ECO代码运行及原理简介

论文地址：https://arxiv.org/pdf/1611.09224.pdf
代码地址：https://github.com/martin-danelljan/ECO
ECO:（Efficient Convolution Operators for Tracking）是CVPR2017的一篇基于相关滤波的文章，本文主要对其matlab版本配置运行进行介绍，并简要分析其跟踪原理，分享自己的一些心得。

一、matlab代码运行

1、matconvnet下载

下载地址： https://github.com/vlfeat/matconvnet
下载后放置到external_libs/matconvnet/目录下

2、PDollar Toolbox下载

下载地址：https://github.com/pdollar/toolbox
下载后放置在external_libs/pdollar_toolbox/目录下

3、预训练模型imagenet-vgg-m-2048.mat下载

下载地址：https://www.vlfeat.org/matconvnet/pretrained/

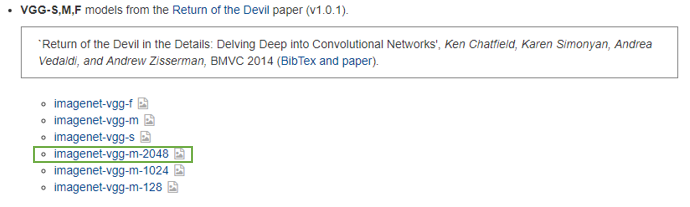
如果点击出现乱码，无法下载，建议换个浏览器下载
在feature_extraction/目录下新建文件夹networks，并将下载的网络放置底下

4、运行install.m

如果是第一次在matlab运行matconvnet可能会比较麻烦点，CPU版本运行详解步骤可以参考我的上一篇博客CCOT代码运行，如果是GPU版本运行可以参考我的另一篇博客SiameseFC的运行两者是一样的流程。如果不想装visual studio，也可以参考这篇博客
运行成功显示如下

5、跟踪

作者给了好几个版本，都可以查看效果

1. demo_ECO----CPU版本
2. demo_ECO_gpu----GPU版本
3. demo_ECO_HC----不使用CNN特征，只使用HOG+CN

三者跟踪速度差距较大，在我的matlab上跟踪速度如下：

跟踪效果如下

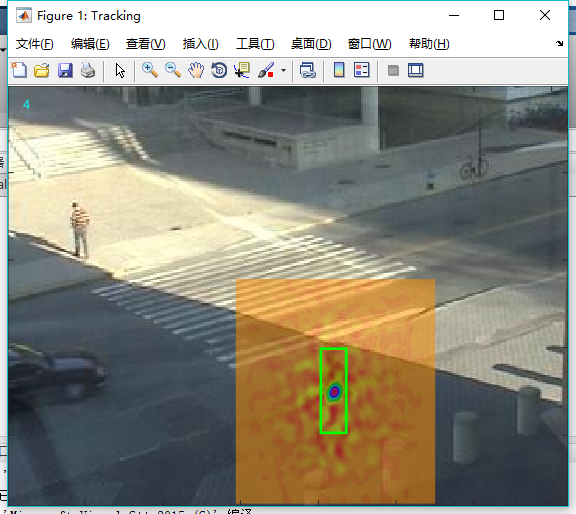
二、ECO算法简介

ECO是在CCOT的基础上进行改进的，两者也是出自同一作者，ECO主要是作者为解决CCOT过拟合、速度慢等问题进行的改进。

2.1背景

基于相关滤波的目标跟踪可以说是这几年的一个重要分支。为提高其跟踪的精度和鲁棒性，人们普遍采用1、多维度特征；2、目标尺寸预测；3、非线性核；4、对前几帧模型的存储；5、复杂的学习模型和6、减少边缘效应等手段，但这些方法都是以牺牲跟踪速度为前提的。
这些手段虽然提高了精度和跟踪鲁棒，但也带来了过拟合的风险。
为什么会过拟合？
目标跟踪通过第一帧来训练模型，训练数据相当有限，可是为了提高跟踪性能，滤波器模板越来越复杂（尤其是深度特征，数据量相当庞大），想利用有限的训练数据形成庞大复杂的训练模型，过分的训练少量的数据，导致复杂模型存在过拟合（以CCOT算法为例，每次更新模型需要改变800,000个参数）
总结起来，影响相关滤波速度的主要有
1、滤波器模型越来越大，不仅给计算带来负担，而且容易引起过拟合。
2、训练集越来越大，训练集主要用于保存之前每一帧的跟踪结果，所以每一次更新滤波器模型时，都要用到之前的样本，那么随着跟踪的进行，训练集保存的样本将越来越多，这明显不实际。一般都是丢弃老的样本，保存新的样本，但这种取舍导致模型更新过于依赖最近几帧目标的外观形状，但出现遮挡等现象，可能会污染模型，导致失败
3、模型更新策略，每帧更新模型不仅耗时，而且容易过拟合

2.2本文的三个贡献

本文主要是提出三个核心点，并解决了三个问题
1、Factorized Convolution Operator–特征的删减
先简要分析一下CCOT，CCOT的核心贡献在于将离散的feature map插值到连续域，解决了不同feature map的尺寸问题。
对离散feature map输入进行插值

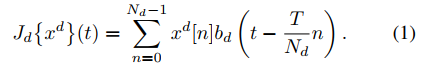
$b_d$实际是一个sinc函数
$x^d[n]$第d维特征对应的离散输入
$N^d$离散输入的数量，或者可以理解为feature map的分辨率
$J^d$插值结果，第d维对应的连续的feature map
滤波器模型预测结果：

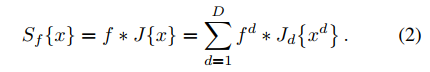
损失函数（共有M个训练样本）

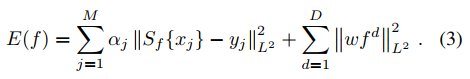
变换到频域

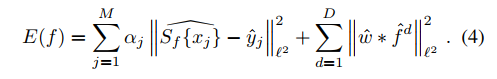
对滤波器f求导，解的

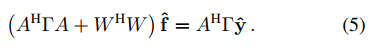
$A$：块对角矩阵，实际就是训练样本组成的矩阵，每个对角块代表一个样本
$\Gamma$:包含每个训练样本权重${\alpha }_j$的矩阵
通过Conjugate Gradient（共轭梯度）迭代计算出使损失函数最小的$\hat{f}$
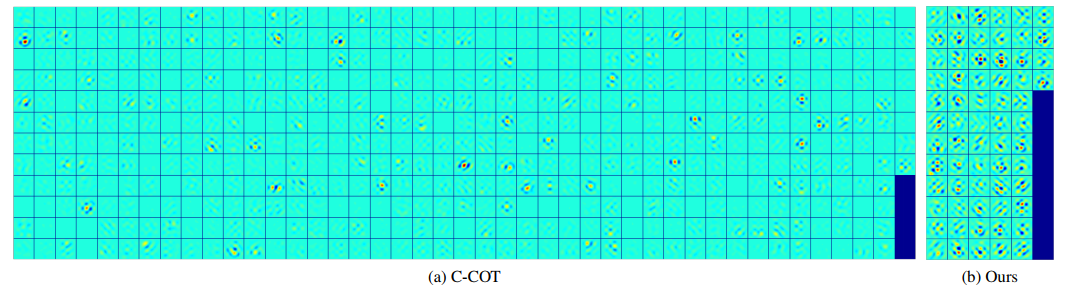
CCOT在特征提取方面相当全面CNN+CN+HOG的组合使得其性能相当出色，但作者很快发现CCOT存在大量的过拟合，如下图

因此，ECO中，作者第一个贡献就是对CCOT特征提取的简化，对于CCOT，每一维特征都对应一个特定的滤波器，但通过观察可以发现，CCOT用到的滤波器很稀疏，如下图所示，绝大部分滤波器对跟踪定位没有帮助却占用计算时间，所以Factorized Convolution Operator就是为了保留对定位有重要贡献的滤波器。

具体步骤：
主要是引入一个常数矩阵P（尺寸为D×C），该矩阵的作用在于将高维特征进行删减，原来共有D维特征，加入P后只剩下C维（P对滤波器数量的删减可以理解为对提取特征维度的删减，因为一个滤波器对应一个特征）。
预测结果：

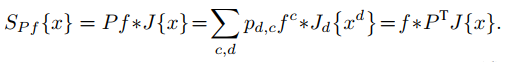
损失函数在频域中表现为：

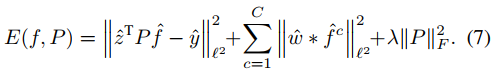
这是一个非线性最小二乘问题，相比于CCOT，作者不仅用了Conjugate Gradient（共轭梯度），还引入高斯牛顿来对矩阵P，滤波器$\hat{f}$进行展开

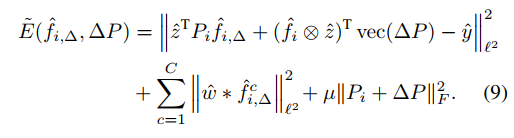
其中

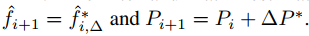
其中高斯牛顿迭代了10次，共轭梯度迭代了20次，具体原理不明白可以不深究。
第一个贡献的效果：明显降低了滤波器的维度数量

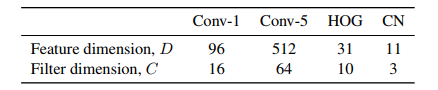
2、Generative Sample Space Model----保持样本的多样性并减少其数量
这一贡献主要是针对训练集进行改进，正如上文所提，训练集数量庞大，而且简单的舍弃老样本（如下图的第二行Baseline所示）导致滤波器模型过于依赖最近几帧的目标外观模型，且存在大量冗余。

为此作者通过样本x和预期目标输出y的联合概率分布p(x,y)，将目标函数完善为

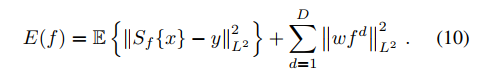
原始的损失函数（公式3）只不过是$p(x,y)={\sum }_{j=1}^M{\alpha }_j{\delta }_{x_j,y_j}(x,y)$的一个特例，另外预期目标输出y其实形状一致，只不过峰值位置发生平移，所以作者将y设置成一样，而峰值位置的平移放入x中进行考虑。所以只需要考虑p(x)，此处引入高斯混合建模（GMM）

高斯混合模型，英文全称：​​Gaussian mixture model，简称GMM。高斯混合模型就是用高斯概率密度函数（二维时也称为：正态分布曲线）精确的量化事物，将一个事物分解为若干基于高斯概率密度函数行程的模型
高斯混合模型也​被视为一种聚类方法，是机器学习中对“无标签数据”进行训练得到的分类结果。其分类结果由概率表示，概率大者，则认为属于这一类。

对GMM模型的理解
类似于傅里叶变换，自然界任何复杂曲线都可以用无数个不同形状sin和cos曲线组成，高斯函数也是如此（如下图，摘自博客），只要数量够多，高斯函数可以表征任意复杂的曲线，换成高维空间也是一个道理。

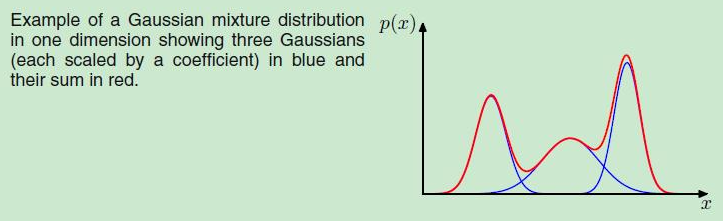
总结一句话，通过多个不同形状的高斯函数（component对应上图中蓝色的单一高斯曲线），可以拟合任意曲线（GMM模型对应上图中红色的高斯叠加曲线）。

训练集采集样本步骤：

1. 每来一帧新图片，使用${\pi }_m=\gamma$和${\mu }_m=x_j$（训练样本输入）来初始化一个新component m
2. 如果此时component的数量超过L（事先设定的值），开始简化GMM模型，反之，直接进行保存
3. 简化GMM，比较GMM各个components的${\mu }_m$，根据两者之间的距离$||{\mu }_k-{\mu }_l$，找出距离最近的两个components，并将其合为一个component，该component的$\mu$和$\pi$由下可计算得
   
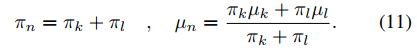
4. 持续更新，直到M个训练样本都结束完

损失函数为

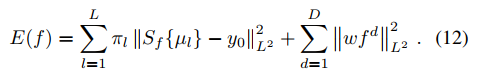
相比原来的损失函数，滤波器由M减为L（文中L=M/8）
3、Model Update Strategy----每6帧更新一次模型
模型更新没什么难理解，每隔$N_s=6$更新一次。
但这里有的需要注意得，那就是训练集样本component仍然是每帧更新的，但是GMM模型是每$N_s$更新一次

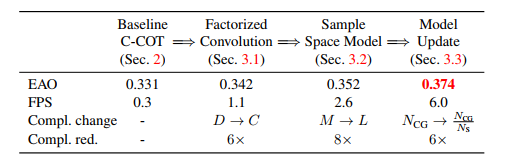
2.3跟踪效果

相比于CCOT，其精度更佳，速度更快，三个贡献都相当有效

参考博客
深度理解高斯混合模型（GMM）
目标跟踪算法二：ECO: Efficient Convolution Operators for Tracking（2016年11月）

最后

以上就是大力毛豆为你收集整理的目标跟踪之ECO代码运行及原理简介的全部内容，希望文章能够帮你解决目标跟踪之ECO代码运行及原理简介所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。