长沙理工大学第十二届ACM大赛 K.大家一起来数二叉树吧【Dp】

题目描述

某一天，Zzq正在上数据结构课。老师在讲台上面讲着二叉树，zzq在下面发着呆。

突然zzq想到一个问题：对于一个n个节点，m个叶子的二叉树，有多少种形态呐？你能告诉他吗？

对于第一组样例的解释

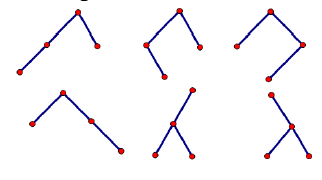
输入描述:

每一组输入一行，两个正整数n,m（n<=50）意义如题目

输出描述:

每一行输出一个数，表示相应询问的答案取模1000000007

示例1

输入

4 2
10 5

输出

6
252

备注:

a取模b等于a%b，即a除以b的余数

思路：

通俗的套路，和这个题很类似：链接

我们设定Dp【i】【j】，表示一颗i个节点的二叉树，其叶子节点数量为j个的方案数。

我们考虑每次合并两颗子树或者延展一颗子树变大来状态转移。也就是从小得到大的一种递推。

那么有：

①Dp【i】【j】+=Dp【i-1】【j】*2（放在左右两边都是一种解。我们这样转移相当于延展出一个根节点，来连接当前这个子树。）

②Dp【i】【j】+=Dp【x】【y】*Dp【a】【b】，这里x+a==i-1&&y+b==j，这样转移相当于延展出一个根节点，让一个子树作为左儿子，另一个作为右儿子，这里不乘2是因为之后xy，和ab我们在枚举的过程中肯定有所交换，所以不需要。

过程维护一下，别忘记取模就没有别的什么了。

Ac代码：

#include<stdio.h>
#include<string.h>
using namespace std;
#define ll long long int
const ll mod=1000000007;
ll dp[150][150];
void init()
{
    int n=50,m=50;
    memset(dp,0,sizeof(dp));
    dp[1][1]=1;
    for(int i=2; i<=n; i++)
    {
        for(int j=1; j<=m; j++)
        {
            dp[i][j]+=dp[i-1][j]*2;
            dp[i][j]%=mod;
            for(int k=1; k<=n&&i-k-1>=0; k++)
            {
                for(int l=1; l<=m&&j-l>=0; l++)
                {
                    dp[i][j]+=dp[k][l]*dp[i-k-1][j-l];
                    dp[i][j]%=mod;
                }
            }
        }
    }
}
int main()
{
    init();
    int n,m;
    while(~scanf("%d%d",&n,&m))
    {
        printf("%lldn",dp[n][m]);
    }
}

最后

以上就是贪玩萝莉为你收集整理的长沙理工大学第十二届ACM大赛 K.大家一起来数二叉树吧【Dp】的全部内容，希望文章能够帮你解决长沙理工大学第十二届ACM大赛 K.大家一起来数二叉树吧【Dp】所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。