matlab fx函数图像,函数的可视化与Matlab作

5. 图形窗口的创建和分割

◆观察：

【    clf，b=2*pi;x=linspace(0,b,50);

for k =1:9

y=sin(k*x);

subplot(3,3,k),plot(x,y),axis([0,2*pi,-1,1])

end                      】

2.1.2多元函数的可视化与空间解析几何(三维图形)

本节通过高等数学的几个例子观察Matlab的三维绘图功能和技巧。

1. 绘制二元函数

◆观察：绘制  的图象，作定义域的裁剪。

◆(1)观察meshgrid指令的效果。

【  a=-0.98;b=0.98;c=-1;d=1;n=10;

x=linspace(a,b,n); y=linspace(c,d,n);

[X,Y]=meshgrid(x,y);

plot(X,Y,'+')  】

★三维绘图指令mesh、meshc、surf。

◆(2)做函数的定义域裁剪，观察上述三维绘图指令的效果。

程序zxy2_4.m

【    clear,clf,

a=-1;b=1;c=-15;d=15;n=20;eps1=0.01;

x=linspace(a,b,n);y=linspace(c,d,n);

[X,Y]=meshgrid(x,y);

for i=1:n                                 %计算函数值z ，并作定义域裁剪

for j=1:n

if (1-X(i,j))

z(i,j)=NaN;                              %作定义域裁剪，定义域以外的函数值为NaN

else

z(i,j)=1000*sqrt(1-X(i,j))^-1.*log(X(i,j)-Y(i,j));

end

end

end

zz=-20*ones(1,n);plot3(x,x,zz),grid off,hold on        %画定义域的边界线

mesh(X,Y,z)                     %绘图，读者可用meshz,  surf,  meshc在此替换之

xlabel('x'),ylabel('y'),zlabel('z'),   box on      %把三维图形封闭在箱体里  】

◆运行了zxy2_4.m 以后，有关向量存储在工作空间中，在此基础上，观察上述等值线绘制指令的运行效果。

【   [cs,h]=contour(X,Y,z,15);  clabel(cs,h,'labelspacing',244)          】

2. 三元函数可视化: slice指令

◆  观察： 绘制三元函数 的可视化图形。

【     clf,x=linspace(-2,2,40); y=x; z=x;

[X,Y,Z]=meshgrid(x,y,z); w=X.^2+Y.^2+Z.^2;

slice(X,Y,Z,w,[-1,0,1],[-1,0,1],[-1,0,1]),colorbar              】

3. 空间曲线及其运动方向的表现：plot3和quiver指令

【    clf,  t=0:0.1:1.5;

Vx=2*t;Vy=2*t.^2;Vz=6*t.^3-t.^2;

x=t.^2;y=(2/3)*t.^3;z=(6/4)*t.^4-(1/3)*t.^3;  %由速度得到曲线

plot3(x,y,z,'r.-'),hold on                               %画飞行轨迹

%算数值梯度，也就是重新计算数值速度矢量，这只是为了编程的方便，不是必须的

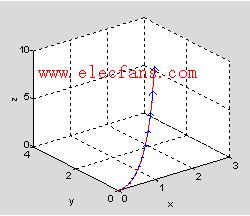
图2.12 飞机的飞行轨迹与方向

Vx=gradient(x);Vy=gradient(y);Vz=gradient(z);

quiver3(x,y,z,Vx,Vy,Vz),grid on        %画速度矢量图

xlabel('x'),ylabel('y'),zlabel('z')      】

2.2应用、思考和练习

2.2.1  线性p周期函数

zxy2_3_f.m

【  function f=zxy2_3_f(x)

f=sin(x+cos(x));               】

zxy2_3.m

【   clear，clf

a=-8;b=12;n=300;xx=linspace(a,b,n);

h=zxy2_3_f(xx);

S(1)=0;

for i=2:n

S(i)=S(i-1)+quad('zxy2_3_f',xx(i-1),xx(i));

end

subplot(1,2,1),plot(xx,S,'k-'),axis([a,b,-1.5,9])

subplot(1,2,2),plot(xx,[h;zeros(1,length(xx))],'k-'),axis([a,b,-1.5,1.5])   】

2.2.2 平面截割法和曲面交线的绘制

◆用平行截面法讨论由曲面     构成的马鞍面形状。

zxy2_6.m ( 平行截割法示例 ， 本程序的绘制两曲面交线方法可以套用)

【  clf, a=-20;eps0=1;

[x,y]=meshgrid(-10:0.2:10);  %生成平面网格

v=[-10 10 -10 10 -100 100];  %设定空间坐标系的范围

colormap(gray)               %将当前的颜色设置为灰色

z1=(x.^2-2*y.^2)+eps;     %计算马鞍面函数z1=z1(x,y)

z2=a*ones(size(x));          %计算平面 z2=z2(x,y)

r0=abs(z1-z2)<=eps0;

%计算一个和z1同维的函数r0,当abs(z1-z2)<=eps时r0 =1；当abs(z1-z2)>eps0时，r0 =0。

%可用mesh(x,y,r0)语句观察它的图形，体会它的作用，该方法可以套用。

zz=r0.*z2;xx=r0.*x;yy=r0.*y; %计算截割的双曲线及其对应的坐标

subplot(2,2,2),     %在第2图形窗口绘制双曲线

h1=plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'+');

set(h1,'markersize',2),hold on,axis(v),grid on

subplot(2,2,1),     %在第一图形窗口绘制马鞍面和平面

mesh(x,y,z1);grid,hold on;mesh(x,y,z2);

h2=plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'.'); %画出二者的交线

set(h2,'markersize',6),hold on,axis(v),

for i=1:5           %以下程序和上面是类似的，通过循环绘制一系列的平面去截割马鞍面

a=70-i*30;      %在这里改变截割平面

z2=a*ones(size(x)); r0=abs(z1-z2)<=1;  zz=r0.*z2;yy=r0.*y;xx=r0.*x;

subplot(2,2,3),

mesh(x,y,z1);grid,hold on;mesh(x,y,z2);hidden off

h2=plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'.'); axis(v),grid

subplot(2,2,4),

h4=plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'o');

set(h4,'markersize',2),hold on,axis(v),grid on

end               】

2.2.3 微分方程的斜率场

◆ 绘制微分方程  的斜率场，并将解曲线画在图中，观察斜率场和解曲线的关系。

zxy2_5.m   ( 绘制一阶微分方程的斜率场和解曲线)

【      clf,clear        %清除当前所有图形窗口的图像，清除当前工作空间的内存变量。

a=0;b=4;c=0;d=4;n=15;

[X,Y]=meshgrid(linspace(a,b,n),linspace(c,d,n));   %生成区域中的网格。

z=X.*Y;                                               %计算斜率函数。

Fx=cos(atan(X.*Y));Fy=sqrt(1-Fx.^2);  %计算切线斜率矢量。

quiver(X,Y,Fx,Fy,0.5),hold on,axis([a,b,c,d])

%在每一网格点画出相应的斜率矢量，0.5是控制矢量大小的控制参数，可以调整。

[x,y]=ode45('zxy2_5f',[0,4],0.4);    %求解微分方程。

%zxy2_5f.m是方程相应函数f(x,y)的程序，单独编制；[x0,xs]=[0,4]为求解区间；

%y0=0.4为初始值；输出变量x,y分别为解轨线自变量和因变量数组。

plot(x,y,'r.-')   %画解轨线  】

zxy2_5f.m (微分方程的函数子程序)

【    function dy=zxy2_5f(x,y)

dy=x.*y;          】

2.2.4颜色控制和渲染及特殊绘图指令

1.地球表面的气温分布(sphere指令)

◆

【 [a,b,c]=sphere(40);t=max(max(abs(c)))-abs(c);surf(a,b,c,t);

axis('equal'),colormap('hot'), shading flat,colorbar   】

2.旋转曲面的生成：柱面指令cylinder和光照控制指令surfl

◆

【       x=0:0.1:10;z=x;y=1./(x.^3-2.*x+4);

[u,v,w]=cylinder(y);surfl(u,v,w,[45,45]);

shading interp    】

3.若干特殊图形

◆ 运行下面程序，了解各指令的用法和效果。

【    x=[1:10]; y=[5 6 3 4 8 1 10 3 5 6];

subplot(2,3,1),bar(x,y),axis([1 10 1 11])

subplot(2,3,2),hist(y,x),axis([1 10 1 4])

subplot(2,3,3),stem(x,y,'k'),axis([1 10 1 11])

subplot(2,3,4),stairs(x,y,'k'),  axis([1 10 1 11])

subplot(2,3,5), x = [1 3 0.5 5];explode = [0 0 0 1];pie(x,explode)

subplot(2,3,6),z=0:0.1:100; x=sin(z);y=cos(z).*10;

comet3(x,y,z)                      】