聚类有效性的评价标准有两种:一是外部标准,通过测量聚类结果和参考标准的一致性来评价聚类结果的优良;另一种是内部指标,用于评价同一聚类算法在不同聚类数条件下聚类结果的优良程度,通常用来确定数据集的最佳聚类数。
一 最佳聚类数判定的方法
对于内部指标,通常分为三种类型:基于数据集模糊划分的指标;基于数据集样本几何结构的指标;基于数据集统计信息的指标。基于数据集样本几何结构的指标根据数据集本身和聚类结果的统计特征对聚类结果进行评估,并根据聚类结果的优劣选取最佳聚类数,这些指标有Calinski-Harabasz(CH)指标,Davies-Bouldin(DB)指标Weighted inter-intra(Wint)指标,Krzanowski-Lai(KL)指标,Hartigan(Hart)指标,In-Group Proportion(IGP)指标等。本文主要介绍Calinski-Harabasz(CH)指标和Davies-Bouldin(DB)指标。
(1) CH指标
CH指标通过类内离差矩阵描述紧密度,类间离差矩阵描述分离度,指标定义为
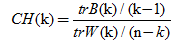
其中,n表示聚类的数目 ,k 表示当前的类, trB(k)表示类间离差矩阵的迹, trW(k) 表示类内离差矩阵的迹。有关公式更详细的解释可参考论文“ A dendrite method for cluster analysis ”。
可以得出 CH越大代表着类自身越紧密,类与类之间越分散,即更优的聚类结果。
(2) DB指标
DB指标通过描述样本的类内散度与各聚类中心的间距,定义为
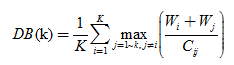
其中,K是聚类数目,Wi表示类Ci中的所有样本到其聚类中心的平均距离,Wj表示类Ci中的所有样本到类Cj中心的平均距离,Cij表示类Ci和Cj中心之间的距离。可以看出,DB越小表示类与类之间的相似度越低,从而对应越佳的聚类结果。
最佳聚类数的确定过程一般是这样的:给定K 的范围[Kmin,Kmax],对数据集使用不同的聚类数K运行同一聚类算法,得到一系列聚类结果,对每个结果计算其有效性指标的值,最后比较各个指标值,对应最佳指标值的聚类数即为最佳聚类数。
二 实验结果
在Matlab中,函数evalclusters提供了四种方法进行聚类效果的评估,包括’CalinskiHarabasz’ 、 ‘DaviesBouldin’ 、’gap’ 、 ‘silhouette’。选取一组数据,进行聚类效果评估。这里分别选用’CalinskiHarabasz’ 、 ‘DaviesBouldin’指标,聚类算法选择k-means.
(1) CH指标
给定K值范围1~3,计算每个聚类结果的CH 指标,最大指标值对应的K 值为最优值。
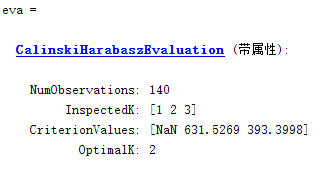
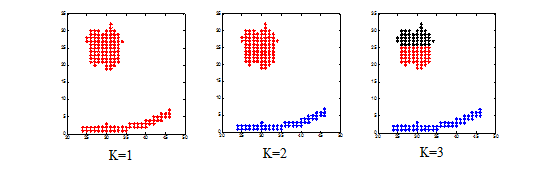
(2) DB指标
给定K值范围1~3,计算每个聚类结果的DB 指标,最大指标值对应的K 值为最优值。
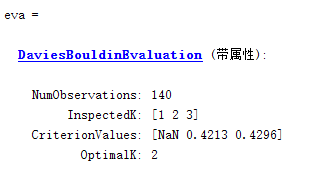
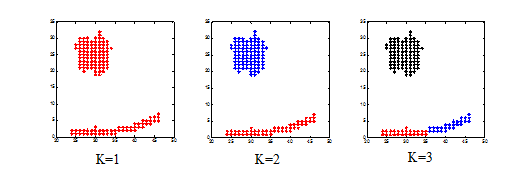
备注:出现NAN是因为这两种方法均不适用与聚类数为1的情况。
Matlab代码
cluster = zeros(size(data,1),3);
for i=1:3
cluster(:,i) = kmeans(data,i,'replicate',5); %%%保存每次聚类结果
end
eva = evalclusters(data,cluster,'DaviesBouldin');
subplot(1,3,1);
plot(data(cluster(:,1)==1,1),data(cluster(:,1)==1,2),'r*');
hold on
subplot(1,3,2);
plot(data(cluster(:,2)==1,1),data(cluster(:,2)==1,2),'r*');
hold on
plot(data(cluster(:,2)==2,1),data(cluster(:,2)==2,2),'b*');
hold on
subplot(1,3,3);
data=[c1 r1];
[idx,ctrs] = kmeans(data,3);
plot(data(cluster(:,3)==1,1),data(cluster(:,3)==1,2),'r*');
hold on
plot(data(cluster(:,3)==2,1),data(cluster(:,3)==2,2),'b*');
hold on
plot(data(cluster(:,3)==3,1),data(cluster(:,3)==3,2),'k*');
hold on
最后
以上就是高贵流沙最近收集整理的关于聚类有效性——最佳聚类数的全部内容,更多相关聚类有效性——最佳聚类数内容请搜索靠谱客的其他文章。








发表评论 取消回复