目录

一、前言

二、问题提出

 三、问题求解

3.1 线性规划（忽视整数条件）

3.2 整数线性规划

3.2.1 对x1进行分枝求解

3.2.2 在x范围下对x2进行分支求解

3.2.3 求解最大值

3.2.4 结果

一、前言

在川川前面两篇的推送中，学习到了如何求解线性规划最大值与最小值问题，但相关参数均以最优形式出现，那么在实际工程问题或者生活中，大部分要求为整数，因此本文将探讨线性整数规划问题。

二、问题提出

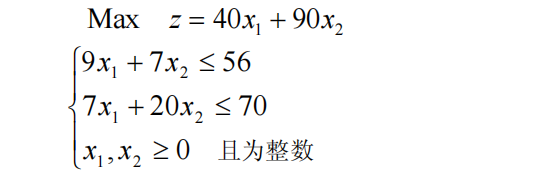
 三、问题求解

3.1 线性规划（忽视整数条件）

忽略整数这一限制条件，即仍为前两天所考虑的线性规划问题，给出如下代码：

clc
clear all
c=[40 90];%目标函数确定
a=[9,7;7,20];
b=[56,70];%两个不等式约束条件
aeq=[];
beq=[];%没有等式约束
lb=[0;0];%大于等于0
ub=[inf;inf];
[x,fval]=linprog(-c,a,b,aeq,beq,lb,ub);
x
best=c*x

运行所得结果如下：

Optimal solution found.


x =

    4.8092
    1.8168


best =

  355.8779

3.2 整数线性规划

在3.1中可以看到，z的最大值为355.9779那么我们可以将z的范围暂定为0≤z≤356，同样由于3.1中未考虑x1和x2的整数问题，而x1在4-5的整数范围内无其他整数，因此需要通过分枝方法来解决。

3.2.1 对x1进行分枝求解

（1）0≤x1≤4情况下代码如下：

clc
clear all
c=[40 90];%目标函数确定
a=[9,7;7,20];
b=[56,70];%两个不等式约束条件
aeq=[];
beq=[];%没有等式约束
lb=[0;0];%大于等于0
ub=[4;inf];%x1的上限改为4，x2没有上限
[x,fval]=linprog(-c,a,b,aeq,beq,lb,ub);
x
best=c*x

结果为：

Optimal solution found.


x =

    4.0000
    2.1000


best =

   349

（2）x1≥5情况下代码如下：

clc
clear all
c=[40 90];%目标函数确定
a=[9,7;7,20];
b=[56,70];%两个不等式约束条件
aeq=[];
beq=[];%没有等式约束
lb=[5;0];%大于等于0
ub=[inf;inf];%x1的上限改为4，x2没有上限
[x,fval]=linprog(-c,a,b,aeq,beq,lb,ub);
x
best=c*x

结果为：

Optimal solution found.


x =

    5.0000
    1.5714


best =

  341.4286

（3）符合条件最大值范围的再次确定：0≤z≤349

3.2.2 在x范围下对x2进行分支求解

（1）在0≤x1≤4情况下,对0≤x2≤2分支情况下代码如下：

clc
clear all
c=[40 90];%目标函数确定
a=[9,7;7,20];
b=[56,70];%两个不等式约束条件
aeq=[];
beq=[];%没有等式约束
lb=[0;0];%大于等于0
ub=[4;2];%x1的上限改为4，x2上限为2
[x,fval]=linprog(-c,a,b,aeq,beq,lb,ub);
x
best=c*x

结果为：

Optimal solution found.


x =

     4
     2


best =

   340

（1）在0≤x1≤4情况下,对x2≥3分支情况下代码如下：

clc
clear all
c=[40 90];%目标函数确定
a=[9,7;7,20];
b=[56,70];%两个不等式约束条件
aeq=[];
beq=[];%没有等式约束
lb=[0;3];%x1大于等于0，x2大于等于3
ub=[4;inf];%x1的上限改为4，x2无上限
[x,fval]=linprog(-c,a,b,aeq,beq,lb,ub);
x
best=c*x

结果为：

Optimal solution found.


x =

    1.4286
    3.0000


best =

  327.1429

（3）符合条件最大值范围的再次确定：340≤z≤349

3.2.3 求解最大值

在前面两步中，我们将x1的范围缩至大于等于5，接下来我们对x2进行分支

(1)0≤x2≤1

clc
clear all
c=[40 90];%目标函数确定
a=[9,7;7,20];
b=[56,70];%两个不等式约束条件
aeq=[];
beq=[];%没有等式约束
lb=[5;0];%x1大于等于5
ub=[inf;1];%x1的上限改为4，x2上限改为1
[x,fval]=linprog(-c,a,b,aeq,beq,lb,ub);
x
best=c*x

结果为：

Optimal solution found.


x =

    5.4444
    1.0000


best =

  307.7778

（2）x2≥2

clc
clear all
c=[40 90];%目标函数确定
a=[9,7;7,20];
b=[56,70];%两个不等式约束条件
aeq=[];
beq=[];%没有等式约束
lb=[5;2];%x1大于等于5，x2大于等于2
ub=[inf;inf];%x1的上限改为4，x2没有上限
[x,fval]=linprog(-c,a,b,aeq,beq,lb,ub);
x
best=c*x

结果为：

No feasible solution found.

Linprog stopped because no point satisfies the constraints.


x =

     []

错误使用  * 
用于矩阵乘法的维度不正确。请检查并确保第一个矩阵中的列数与第二个矩阵中的行数
匹配。要执行按元素相乘，请使用 '.*'。
 
>> 

在此条件下并无解。

3.2.4 结果

综上所述，整个题目最优解为x1=4,x2=2时，zmax=340.

最后

以上就是天真星月为你收集整理的跟着川川学数模-Day2一、前言二、问题提出 三、问题求解的全部内容，希望文章能够帮你解决跟着川川学数模-Day2一、前言二、问题提出 三、问题求解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。