R语言第七讲 线性回归分析案例

题目

          MASS 库中包含 Boston (波士顿房价)数据集，它记录了波士顿周围 506 个街区的 medv (房价中位数)。我们将设法用 13 个预测变量如 rm (每栋住宅的平均房间数)， age (平均房 龄)， lstat (社会经济地位低的家庭所占比例)等来预测 medv (房价中位数)。

************************************************MASS是R语言自带的库********************************************************

library(MASS) #加载MASS程序包
library(ISLR) #加载ISLR程序包，确保事先已经下载install.packages("ISLR")
fix(Boston) #打开Boston房价数据，excel
names(Boston) #查看所有的数据特征，即：列属性
# [1] "crim"    "zn"      "indus"   "chas"    "nox"     "rm"     
# [7] "age"     "dis"     "rad"     "tax"     "ptratio" "black"  
# [13] "lstat"   "medv"  
?Boston#查看Boston的更多数据信息(帮助文档)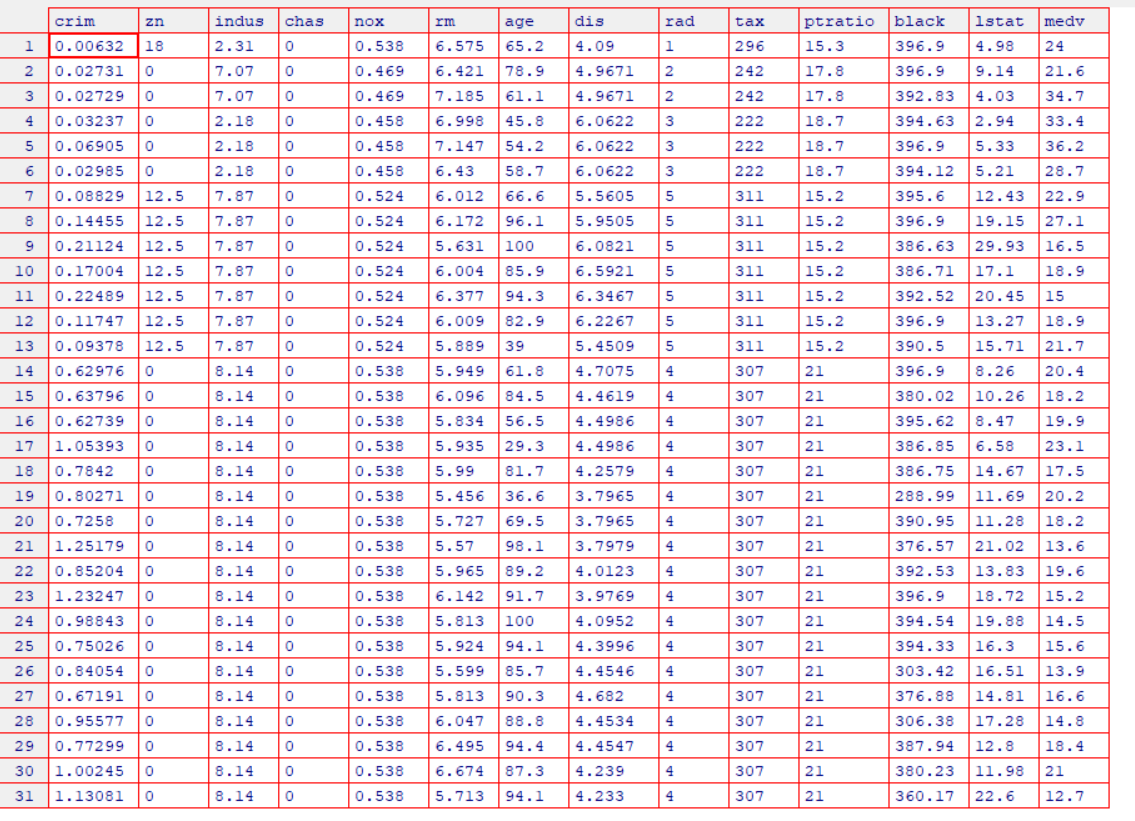

       准备好了数据集，我们开始用 lm ()函数拟合一个简单线性回归模型开始，将 lstat 作为预测变量， medv 作 为响应变量。基本句法是 lm (y ~ x , data) ，其中 y 是响应变量， x 是预测变量， data 是这 两个变量所属的数据集。

lm.fit=lm(medv~lstat)

       发现提示错误：Error in eval(predvars, data, env) : 找不到对象'medv'

因为 R 不知道哪里可以找到变量 medv 和 lstat。下一行命令告诉 R，变 量在 Bosto日数据集中。如果绑定 Boston 数据集， R 就能识别变量，此时第一行语句可以正 常工作。

lm.fit=lm(medv~lstat,data=Boston)
attach(Boston)
lm.fit=lm(medv~lstat)
lm.fit

# Call:
# lm(formula = medv ~ lstat)

# Coefficients : 系数
# (Intercept)        lstat  
#       34.55        -0.95 

       如果我们输入 lm. fit ，则会输出模型的一些基本信息，这给出了预测的线性函数的截距以及系数。那么预测的线性函数就已经出来了。

summary(lm.fit)
Call:
lm(formula = medv ~ lstat)

Residuals:      残差
    Min      1Q  Median      3Q     Max 
-15.168  -3.990  -1.318   2.034  24.500 

Coefficients: 
            Estimate Std. Error t value Pr(>|t|)   #估计标准误差t值 
(Intercept) 34.55384    0.56263   61.41   <2e-16 ***
lstat       -0.95005    0.03873  -24.53   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 6.216 on 504 degrees of freedom #预测的残差标准误 

#Coefficient of determination(有的译为“决定性系数”)。 
Multiple R-squared:  0.5441,	Adjusted R-squared:  0.5432  

#F统计量  P值
F-statistic: 601.6 on 1 and 504 DF,  p-value: < 2.2e-16

这一句会列出系数的p值和标准误，以及模型R^2统计量和F统计量。

Residuals:      残差
    Min      1Q  Median      3Q     Max 
-15.168  -3.990  -1.318   2.034  24.500 

上方的代表残差。 通过将预测结果(通过函数计算）  减去  对应的目标变量 (预测变量的真实值）的真实值，便可获得残差值。

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

       显著性标记   * * * 极度显著，* * 高度显著，*显著，圆点不太显著，没有记号不显著简而言之，*越多代表效果越好，下面估计的系数，代表就极度显著，就是很准确的意思。

Coefficients: 
            Estimate Std. Error t value Pr(>|t|)   #估计标准误差t值 
(Intercept) 34.55384    0.56263   61.41   <2e-16 ***
lstat       -0.95005    0.03873  -24.53   <2e-16 ***

      第一列代表34.55384代表的是截距，-0.95005代表斜率
      第二列：推算的系数的标准差
      第三列：t值，t统计量
      第四列：p值，是一个验证假设是否成立的值。比如身高体重模型，假设身高height与weight无关系，也就是在原始的模型中呢，体重=常数+0*height，height前面系数为0，由此我们可以通过R算出一个统计量t值，Pr表示t值以外的面积，也就是下面谈到的p值

    估计标准误差（Se）是说明实际值与其估计值之间相对偏离程度的指标，主要用来衡量回归方程的代表性。估计标准误差，即因变量y的实际值与回归方程求出的估计值之间的标准误差，估计标准误差越小，回归方程拟合程度越好。

估计标准误差的值越小，则估计量与其真实值的近似误差越小，但不能认为估计量与真实值之间的绝对误差就是估计标准误差。估计标准误差与判定系数相反，se反映了预测值与真实值之间误差的大小，se越大说明拟合度越低。

Residual standard error: 6.216 on 504 degrees of freedom #预测的残差标准误

       残差标准误即计算标准误的样本是样本数值的残差。

       标准误，即样本均数的标准差，是描述均数抽样分布的离散程度及衡量均数抽样误差大小的尺度，反映的是样本均数之间的变异。标准误不是标准差，是多个样本平均数的标准差。

标准误用来衡量抽样误差。标准误越小，表明样本统计量与总体参数的值越接近，样本对总体越有代表性，用样本统计量推断总体参数的可靠度越大。因此，标准误是统计推断可靠性的指标。

#Coefficient of determination(有的译为“决定性系数”)。 
Multiple R-squared:  0.5441,	Adjusted R-squared:  0.5432  

       这里的决定性系数R方，我经常与函数的相关系数R弄混，今天将两者简单谈一下。

1、 相关系数 R

      定义： 变量之间线性相关的度量。

      计算：

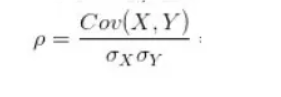
解释：

自变量X和因变量Y的协方差/标准差的乘积。
* 协方差：两个变量变化是同方向的还是异方向的。X高Y也高，协方差就是正，相反，则是负。
* 为什么要除标准差：标准化。即消除了X和Y自身变化的影响，只讨论两者之间关系。
* 因此，相关系数是一种特殊的协方差。

2、决定性系数 R方

      定义：对模型进行线性回归后，评价回归模型系数拟合优度。

      公式：R方=(TSS-RSS)/TSS=1-RSS/TSS 

                 TSS (total sum of squares)：总平方和,即：用真实值-真实值的平均值的平方 

                                                               
                 RSS (regression sum of squares)：残差平方和

                                                                 
          在简单回归模型中，R方是响应变量Y和预测变量X相关系数的平方.在多元线性回归中，是响应值Y和线性拟合值，相关系数的平方。

          综上：R方接近于1，则表明该模型能解释大部分响应变量的方差。

#F统计量  P值
F-statistic: 601.6 on 1 and 504 DF,  p-value: < 2.2e-16

 1、 P值

        P值即概率，反映某一事件发生的可能性大小。统计学根据显著性检验方法所得到的P 值，一般以P < 0.05 为有统计学差异， P<0.01 为有显著统计学差异，P<0.001为有极其显著的统计学差异。其含义是样本间的差异由抽样误差所致的概率小于0.05 、0.01、0.001。实际上，P值不能赋予数据任何重要性，只能说明某事件发生的几率。统计结果中显示Pr > F，也可写成Pr( >F)，P = P{ F0.05 > F}或P = P{ F0.01 > F}。

      计算：

      一般呢，我们进行线性拟合时：拟合出来的公式为 Y(预测） =  b(预测) + a(预测）x  。

但是b(预测)与真实的b会有一定误差，a(预测)也如此，差距如何衡量？

      计算a，b的标准误差可以使用以下公式   

        σ 是变量 Y 的每个实现值 Yi 的标准差。

        计算p值，还需要引入t统计量。

        t统计量

         定义：用于测量 了 β1 偏离 0 的标准偏差。即：测量函数是一个常数函数还是一个一元函数。

         计算：  

         以0为中心，左右对称的单峰分布；t分布是一簇曲线，其形态变化与n（确切地说与自由度df）大小有关。自由度df越小，t分布曲线越低平；自由度df越大，t分布曲线越接近标准正态分布（u分布）曲线；随着自由度逐渐增大，t分布逐渐接近标准正态分布。

      （自由度：估计的样本数据中有n个点，其中有a个点的取值不受其他点的影响，则自由度为a，所谓受影响即：变量x的取值如果不会影响的变量z的取值，比如z不是根据x来计算出来的。那么称z与x没有关系，则没有影响）

        P值定义： 计算任意观测值大于等于 I t I 的概率就十分简单了，我们称这个概率为 p 值 。

        解释：:一个很小的 p 值表示，在预测变量和响应变量之间的真实关系 未知的情况下，不太可能完全由于偶然而观察到预测变量和响应变量之间的强相关。因此，如 果看到一个很小的 p 值，就可以推断预测变量和响应变量问存在关联。

  2、F统计量

       F统计量定义：用来检测响应变量Y与预测变量X之间是否有关系。对于多元一次函数分析用了超过一个参数的统计模型，以                                 判断该模型中的全部或一部分参数是否适合用来估计母体。

       计算：     

               这里把选择忽略的变量放在了列表末尾。在这种情况下，我们用除最后 q 个变量 之外的所有变量建立第二个模型。假                   设该模型的残差平方为 RSSo 

       解释：当响应变量与预测变量时F统计量应该接近于1。

       回到实验，我们可以使用names ()函数找出 lm. fit 中存储的其他信息。虽然可以用名称提取这些量 例 如: lm. fit $ coefficients但用提取功能如 coef ()访问它们会更安全。

 > names(lm.fit)
 [1] "coefficients"  "residuals"     "effects"       "rank"         
 [5] "fitted.values" "assign"        "qr"            "df.residual"  
 [9] "xlevels"       "call"          "terms"         "model"    
> coef(lm.fit)#这样访问更加安全
(Intercept)       lstat 
 34.5538409  -0.9500494 

> confint(lm.fit)#得到系数估计值的置信区间
                2.5 %     97.5 %
(Intercept) 33.448457 35.6592247  #截距估计
lstat       -1.026148 -0.8739505  #一次项系数估计

> predict(lm.fit,data.frame(lstat=(c(5,10,15))), interval="confidence")#计算置信区间
       fit      lwr      upr
1 29.80359 29.00741 30.59978
2 25.05335 24.47413 25.63256
3 20.30310 19.73159 20.87461
> predict(lm.fit,data.frame(lstat=(c(5,10,15))), interval="prediction")#计算预测区间
       fit       lwr      upr
1 29.80359 17.565675 42.04151
2 25.05335 12.827626 37.27907
3 20.30310  8.077742 32.52846

         由以上数据可以看出：如当 lstat 等于 10 时，相应的 95% 置信区间为 (24. 47 , 25. 63) ，相应的 95% 预测区 间为 (12.828 ， 37.28) 。正如预期的那样，置信区间和预测区间有相同的中心点(当 lstat 等于 10 时， medv 的预测值是 25.05) ，但后者要宽得多。 

       用函数 plot ()和 abline ()绘制 medv 和 lstat 的散点图以及最小二乘回归 直线。 

plot(lstat,medv)
abline(lm.fit)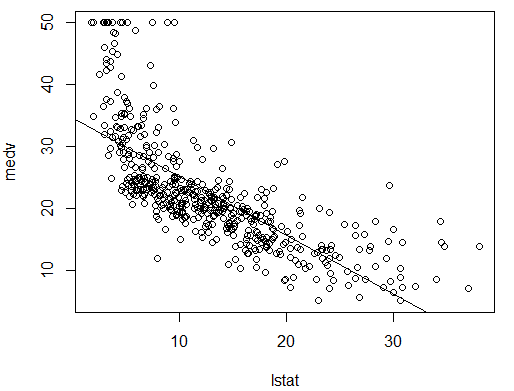

abline(lm.fit,lwd=3)
abline(lm.fit,lwd=3,col="red")
plot(lstat,medv,col="red")
plot(lstat,medv,pch=20)
plot(lstat,medv,pch="+")
plot(1:20,1:20,pch=1:20)

  以上命令，分别是改变线条的宽度，线的颜色，散点图的点的形状，点的大小、颜色等。

     接下来我们检查一些诊断图。对lm ( )的输出直接用 plot ()命令将自动生成四幅诊断图。一般情况下，这个命令每次生成一幅图，按下回车键 (Enter) 将生成下一幅图。然而，同时查看所有 4 幅图通常比较方便。可以用 par ()函数做到 这一点，它指示 R 将显示屏分割成独立的面板，所以可以同时查看多个图。例如， par (mfrow = c (2 , 2)) 把绘图区域划分成 2 x2 的网格面板。

par(mfrow=c(2,2))
plot(lm.fit)#生成4幅诊断图
plot(predict(lm.fit), residuals(lm.fit))
plot(predict(lm.fit), rstudent(lm.fit))

plot(hatvalues(lm.fit))
which.max(hatvalues(lm.fit))
375 
375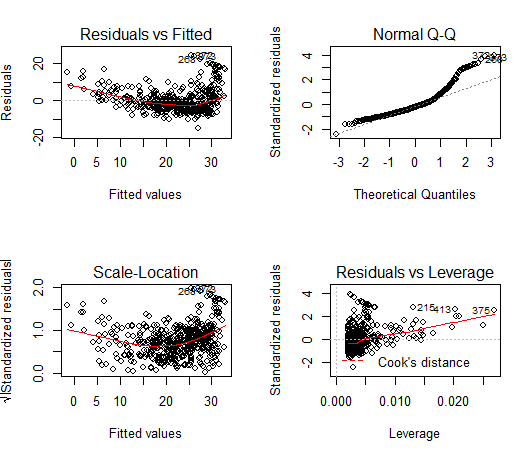 

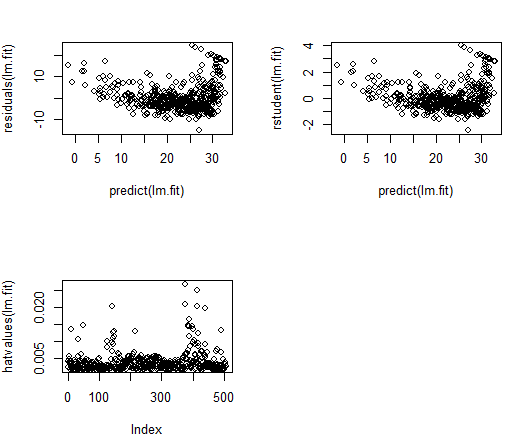
      以用 residuals ()函数计算线性回归拟合的残差。函数 rstudent ()可计算学生化 残差，我们也可以用这个函数绘制残差对拟合值的散点图。

      残差图中的一些证据表明数据有非线性。杠杆统计量可以由 hatva1ues ()函数为任意多 个预测变量来计算。

      which. max ()函数可识别出向量中最大元素的索引。在本例中，它告诉我们哪个观测具 有最大的杠杆统计量。


                 

最后

以上就是自觉月光为你收集整理的R语言第七讲 线性回归分析案例的全部内容，希望文章能够帮你解决R语言第七讲 线性回归分析案例所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。