1.2.2 十进制数转换成非十进制数
十进制数转换成非十进制数的方法是:整数部分的转换用“除基取余法”,也就是用基数相除,然后反序(由后向前取)取余数;小数部分的转换用“乘基取整法”,也就是用基数相乘,然后正序(由前向后取)取整数。这里的“基数”就是对应的数制,如二进制的基数为2,八进制的基数为8,十六进制的基数为16。
1.十进制转换为二进制
这里分别对十进制整数和十进制小数转换成二进制进行介绍。
1)十进制整数转换成二进制的方法
十进制整数转换为二进制的方法是:采用“除2逆序取余”法(采用短除法进行)。也就是先将十进制数除以2,得到一个商数(也是下一步的被除数)和余数;然后再将商数除以2,又得到一个商数和余数;以此类推,直到商数为小于2的数为止。然后从最后一步得到的小于2的商数开始将其他各步所得的余数(也都是小于2的0或1)排列起来(俗称“逆序排列”)就得到了对应的二进制数。
注意 这里与下面的小数转换有些不一样,这里要包括最后得到的小于2的商数,而小数转换中是不需要包括最后的积的,只包括各步得到的整数部分,后面的十进制整数转换为八进制、十六进制也一样。
图1-1所示为十进制整数48转换成二进制数时依次除2的过程,在每步的最右边显示的是各步商数除2所得到的余数,最后一步的商数为1,因为它小于2,所以不能再除了。然后从最后得到商数(1)开始依次向上把其他各步除2得到的余数排列起来,就得到最后48转换成二进制时的结果为(110000)2。同理,图1-2所示的十进制数250转换成二进制数后的结果就为(11111010)2。
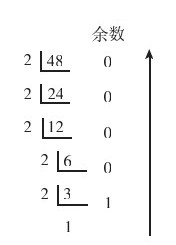
图1-1 十进制整数48转换成二进制整数的步骤
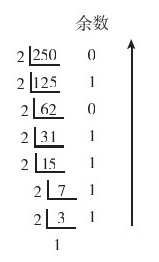
图1-2 十进制整数250转换成二进制整数的步骤
2)十进制小数转换成二进制的方法
十进制小数转换为二进制的方法是采用“乘2正序取整”法。也就是用2乘十进制小数,得到一个积,然后将积的整数部分取出作为相应步骤得到的整数;再用2乘余下的小数部分,又得到一个积;然后再将这个积的整数部分取出;以此类推,直到积中的小数部分为零,或者达到所要求的精度为止;最后把各步取出的整数部分(仅需要各步得到的整数部分,不需要最后没有取整的小数部分)按正序排列起来,即先取的整数作为二进制小数的高位,后取的整数作为低位。
图1-3的左、右图是分别将十进制小数0.125和0.625转换成二进制的过程,最后得到的二进制数就是从最开始得到的整数值开始,一直到最后得到的整数值(也就是自上而下的顺序,与整数转换中取余的顺序相反)。0.125和0.625最后的二进制值分别为(0.001)2和(0.101)2(注意,一定要记得在整数部分加上“0.”,因为十进制小数转换成二进制后仍是小数)。
注意 有些十进制小数乘以2后是个无穷循环数,永远不会有完整的整数,此时就要看所需的精度如何了,按所需位数精度取值即可。如0.825就是这样一个数,如果仅要求是小数点后3位,则相应的二进制数为(0.110)2,如果要求为4位,则对应的二进制值为(0.1101)2。具体如图1-4所示。
如果一个十进制同时有整数和小数部分,则要对整数和小数部分分别按以上介绍的对应方法进行二进制转换。
2.十进制转换成八进制
八进制数的基数为8,因此八进制数中的数码有0、1、2、3、4、5、6、7,共八个。十进制转换成八进制的方法与前面介绍的十进制数转换成二进制的方法类似,只不过这里的基数是8(而不再是2)。十进制转换成八进制当然也分整数部分和小数部分两种不同的转换方法。
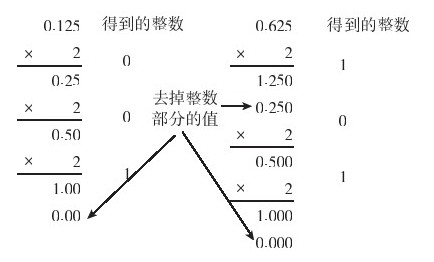
图1-3 0.125和0.625十进制小数转换成二进制小数的步骤

图1-4 不同精确度要求的取值示例
十进制整数转换为八进制整数采用“除8逆序取余”的方法,直到所得的商小于8,然后把余数(包括最后一步中得到的小于8的商数)按逆序排列即可;十进制小数转换为八进制小数是采用“乘8正序取整”法,直到所得到的积小数部分为0,或者在规定的精度范围内,然后把所得到的整数正序排列起来即可。
图1-5左、右图是分别将十进制整数65和2467按“除8逆序取余”的方法转换成八进制的步骤,得到的结果分别是(101)8和(463)8。
图1-6左、右图所示的是两个十进制小数0.125和0.8125通过“乘8正序取整”的方法转换成八进制的步骤,得到的结果分别是(0.1)8和(0.64)8(是正序排列,一定要记得在整数部分加上“0.”)。
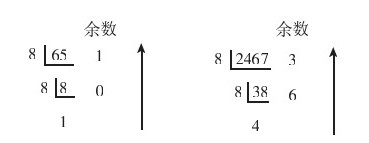
图1-5 两个十进制整数转换成八进制整数的步骤

图1-6 两个十进制小数转换成八进制小数的步骤
3.十进制转换成十六进制
十六进制数的基数为16,十六进制数中的数码有0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F,共十六个。
十进制转换成十六进制与十进制转换成二进制类似,将十进制整数转换为十六进制的方法是采用“除16逆序取余”法,直到所得的商小于16,然后把余数(包括最后一步中得到的小于16的商数)按逆序排列即可;十进制小数转换为十六进制的方法是采用“乘16正序取整”法,直到所得到的积小数部分为0,或者在规定的精度范围内,然后把所得到的整数正序排列起来即可。
图1-7左、右图是分别将十进制整数45和3456按“除16逆序取余”的方法转换成十六进制的步骤,得到的结果分别是(2D)16和(D80)16(注意,其中的13用十六进制的D表示了)。
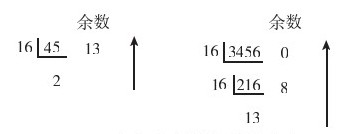
图1-7 两个十进制整数转换成十六进制整数的步骤
图1-8左、右图是将十进制小数0.125和0.825通过“乘16正序取整”的方法转换成十六进制的步骤,得到的结果分别是(0.2)16和(0.D33)16(精确到小数点后面三位)(注意:是正序排列,也一定要记得在整数部分加上“0.”,仍是小数)。

图1-8 两个十进制小数转换成十六进制小数的步骤
4.同步练习
1)把十进制数825、10815.6转换成二进制;
2)把十进制数658、9240.65转换成八进制;
3)把十进制数2508、5420.82转换成十六进制。
最后
以上就是犹豫汉堡最近收集整理的关于深入了解计算机网络,《深入理解计算机网络》的全部内容,更多相关深入了解计算机网络内容请搜索靠谱客的其他文章。








发表评论 取消回复