概述
最近在做传感器融合方面的研究，但相关的资料甚少，想着分解一块一块地实现（补充知识），总之道阻且长，一步步来叭
坐标系转换
世界坐标系
由于摄像机与被摄物体可以放置在环境中的任意位置，这样就需要在环境中建立一个坐标系，来表示摄像机和被摄物体的位置，这个坐标就称为世界坐标系
相机坐标系
也是一个三维直角坐标系，原点位于镜头的光心处，x,y轴分别与相面的两边平行，z轴为镜头的光轴，与像平面垂直
世界坐标系到相机坐标系
旋转
旋转的表示
- 旋转矩阵
- 欧拉角
- 四元数
- 轴角
- 李群与李代数
旋转的应用场景
惯性导航 机器人学 （机械臂，无人机，SLAM)
步骤
- 先旋转对齐
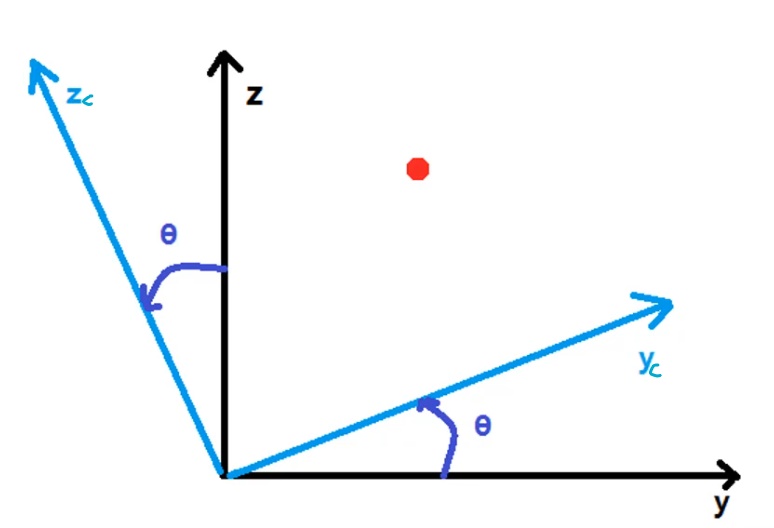
[ x c y c z c ] = [ 1 0 0 0 cos θ sin θ 0 − sin θ cos θ ] [ x y z ] begin{bmatrix} x_{c} \ y_{c} \ z_{c} end{bmatrix}=begin{bmatrix} 1 & 0 & 0 \ 0 & cos theta & sin theta \ 0 & -sin theta & cos theta end{bmatrix}begin{bmatrix} x \ y \ z end{bmatrix} ⎣⎡xcyczc⎦⎤=⎣⎡1000cosθ−sinθ0sinθcosθ⎦⎤⎣⎡xyz⎦⎤
具体推导
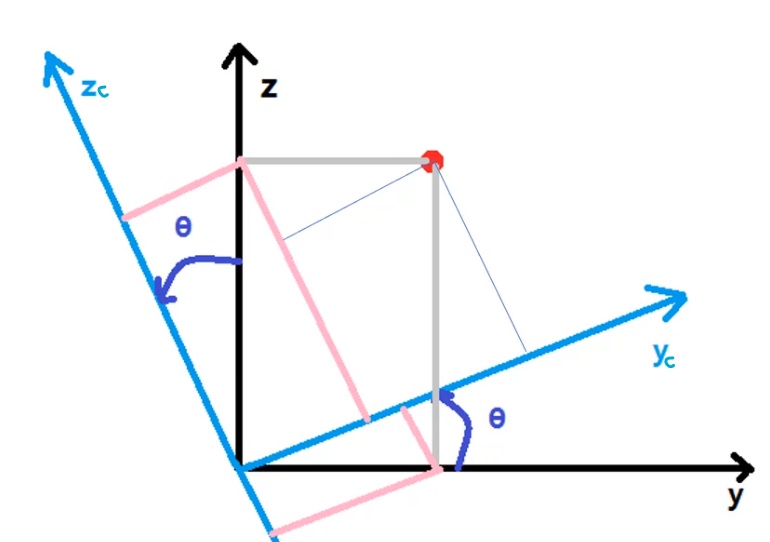
{ X c = X Y c = cos θ ⋅ Y + sin θ ⋅ Z Z c = − sin θ ⋅ Y + cos θ ⋅ Z begin{cases}X_{c}=X\ Y_{c}=cos theta cdot Y+sin theta cdot Z\ Z_{c}=-sin theta cdot Y+cos theta cdot Zend{cases} ⎩⎪⎨⎪⎧Xc=XYc=cosθ⋅Y+sinθ⋅ZZc=−sinθ⋅Y+cosθ⋅Z
所有的分解都满足欧式距离不变性
其他旋转矩阵
- 绕X轴
R ( X A , θ ) = [ 1 0 0 0 cos θ − sin θ 0 sin θ cos θ ] Rleft( X_{A},theta right) =begin{bmatrix} 1 & 0 & 0 \ 0 & cos theta & -sin theta \ 0 & sin theta & cos theta end{bmatrix} R(XA,θ)=⎣⎡10 00cosθsinθ0−sinθcosθ⎦⎤ - 绕Y轴
R ( Y A , θ ) = [ cos θ 0 sin θ 0 1 0 − sin θ 0 cos θ ] Rleft( Y_{A},theta right) =begin{bmatrix} cos theta & 0 & sin theta \ 0 & 1 & 0 \ -sin theta & 0 & cos theta end{bmatrix} R(YA,θ)=⎣⎡cosθ0 −sinθ010sinθ0cosθ⎦⎤ - 绕Z轴
R ( Z A , θ ) = [ cos θ − sin θ 0 sin θ cos θ 0 0 0 1 ] Rleft( Z_{A},theta right) =begin{bmatrix} cos theta & -sin theta & 0 \ sin theta & cos theta & 0 \ 0 & 0 & 1 end{bmatrix} R(ZA,θ)=⎣⎡cosθsinθ 0−sinθcosθ0001⎦⎤
把三个绕不同方向的旋转进行相乘
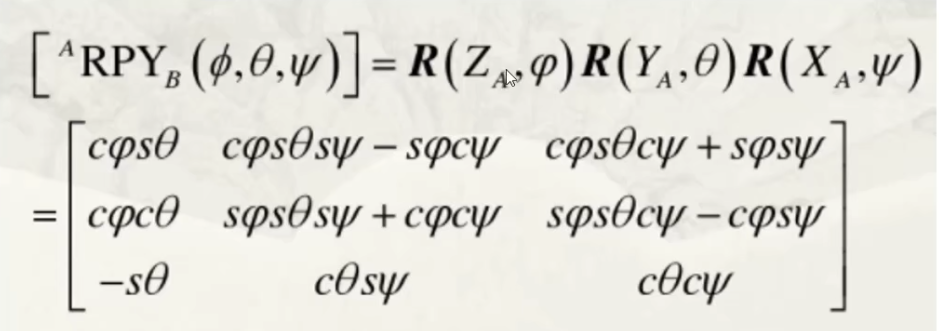
这样可以表示空间中任意方向中的旋转
左乘还是右乘
- 左乘：相对于固定坐标系进行变换
V ′ = R × V = ( R Z × R Y × R X ) × V V'=Rtimes V=left( R_{Z}times R_{Y}times R_{X}right) times V V′=R×V=(RZ×RY×RX)×V
对每个固定的坐标系进行变换 - 右乘：相对于自身（活跃/变化）的坐标系进行变换
每一次变换后按新的（自身的）坐标系进行变换
详细参考这篇文章
旋转的左乘与右乘
平移
我们把旋转矩阵称为R，T为X,Y,Z三轴方向的平移，（R，T即为相机的外参）
[
X
c
Y
c
Z
c
]
=
R
[
X
w
Y
w
Z
w
]
+
T
begin{bmatrix} X_{c} \ Y_{c} \ Z_{c} end{bmatrix}=Rbegin{bmatrix} X_{w} \ Y_{w} \ Z_{w} end{bmatrix}+T
⎣⎡XcYcZc⎦⎤=R⎣⎡XwYwZw⎦⎤+T
= [ r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 ] [ X w Y w Z w ] + [ t x t y t z ] =begin{bmatrix} r_{11} & r_{12} & r_{13} \ r_{21} & r_{22} & r_{23} \ r_{31} & r_{32} & r_{33} end{bmatrix}begin{bmatrix} X_{w} \ Y_{w} \ Z_{w} end{bmatrix}+begin{bmatrix} tx \ ty \ tz end{bmatrix} =⎣⎡r11r21r31r12r22r32r13r23r33⎦⎤⎣⎡XwYwZw⎦⎤+⎣⎡txtytz⎦⎤
齐次方程形式
[
x
c
y
c
z
c
1
]
=
[
R
t
0
1
]
[
x
w
y
w
z
w
1
]
begin{bmatrix} x_{c}\ y_{c} \ z_{c} \ 1 end{bmatrix}=begin{bmatrix} R & t \ 0 & 1 end{bmatrix}begin{bmatrix} x_{w} \ y_{w} \ z_{w} \ 1 end{bmatrix}
⎣⎢⎢⎡xcyczc1⎦⎥⎥⎤=[R0t1]⎣⎢⎢⎡xwywzw1⎦⎥⎥⎤
总结
- 世界坐标系变换到相机坐标系，是为了将像素点与世界点联系起来
- 世界点：我们需要待测量物体到机器人的距离和位置关系，世界坐标系一般定在机器人上，或者是机器人工作的场景之中
- 世界坐标系与相机坐标系的关系就是相机的外参
最后
以上就是沉默黄豆为你收集整理的Sensor fusion学习-1.坐标系转换理论坐标系转换的全部内容，希望文章能够帮你解决Sensor fusion学习-1.坐标系转换理论坐标系转换所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复