Outlier Detection异常检测算法学习笔记基于统计学的方法基于相似度的方法集成方法

63 阅读 0 评论 42 点赞

我是靠谱客的博主心灵美帽子，最近开发中收集的这篇文章主要介绍Outlier Detection异常检测算法学习笔记基于统计学的方法基于相似度的方法集成方法，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

基于统计学的方法

HBOS

1.Histogram-based Outlier Score。它是⼀种单变量⽅法的组合，不能对特征之间的依赖关系进⾏建模，但是计算速度较快，对⼤数据集友好。其基本假设是数据集的每个维度相互独⽴。然后对每个维度进⾏区间(bin)划分，区间的密度越⾼，异常评分越低。
2.为每个数据维度做出数据直⽅图。对分类数据统计每个值的频数并计算相对频率。
3.对每个维度都计算了⼀个独⽴的直⽅图，其中每个箱⼦的⾼度表⽰密度的估计。然后为了使得最⼤⾼度为1（确保了每个特征与异常值得分的权重相等），对直⽅图进⾏归⼀化处理。最后，每⼀个实例的HBOS值由以下公式计算：

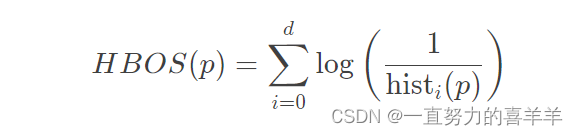
在这里插入图片描述

HBOS这个算法原理简单，复杂度低，在大数据场景比较好用，但是异常识别的效果一般，且针对特征间比较独立的场景，简单点讲该算法就是把数据划分为多个区间，然后根据每个区间的频次根据概率密度函数转化为对应的出现概率，在将这个概率转化为异常分数，以此来区分异常数据

因此HBOS在全局异常检测问题上表现良好，但在局部异常的检测上效果一般。

链接：https://blog.csdn.net/fengdu78/article/details/124013405?spm=1001.2101.3001.6661.1&utm_medium=distribute.pc_relevant_t0.none-task-blog-2%7Edefault%7ECTRLIST%7Edefault-1-124013405-blog-112687881.pc_relevant_aa&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-2%7Edefault%7ECTRLIST%7Edefault-1-124013405-blog-112687881.pc_relevant_aa&utm_relevant_index=1

链接:https://blog.csdn.net/qq_35692819/article/details/112687881

基于相似度的方法

基于簇的检测

如DBSCAN等聚类算法
聚类的主要目的通常是为了寻找成簇的数据，而将异常值和噪声一同作为无价值的数据而忽略或丢弃，在专门的异常点检测中使用较少。
聚类算法的优缺点：
（1）能够较好发现小簇的异常；
（2）通常用于簇的发现，而对异常值采取丢弃处理，对异常值的处理不够友好；
（3）产生的离群点集和它们的得分可能非常依赖所用的簇的个数和数据中离群点的存在性；
（4）聚类算法产生的簇的质量对该算法产生的离群点的质量影响非常大。

基于距离的度量

如k近邻算法
为了使模型更加稳定，距离值的计算通常使用k个最近邻的平均距离。
k近邻算法的优缺点：
（1）简单；
（2）基于邻近度的方法需要O(m2)时间，大数据集不适用；
（3）对参数的选择敏感；
（4）不能处理具有不同密度区域的数据集，因为它使用全局阈值，不能考虑这种密度的变化。

基于密度的度量

如LOF（局部离群因子）算法
局部离群因子（LOF）算法与k近邻类似，不同的是它以相对于其邻居的局部密度偏差而不是距离来进行度量。它将相邻点之间的距离进一步转化为“邻域”，从而得到邻域中点的数量（即密度），认为密度远低于其邻居的样本为异常值。
LOF（局部离群因子）算法的优缺点：
（1）给出了对离群度的定量度量；
（2）能够很好地处理不同密度区域的数据；
（3）对参数的选择敏感。
可达距离

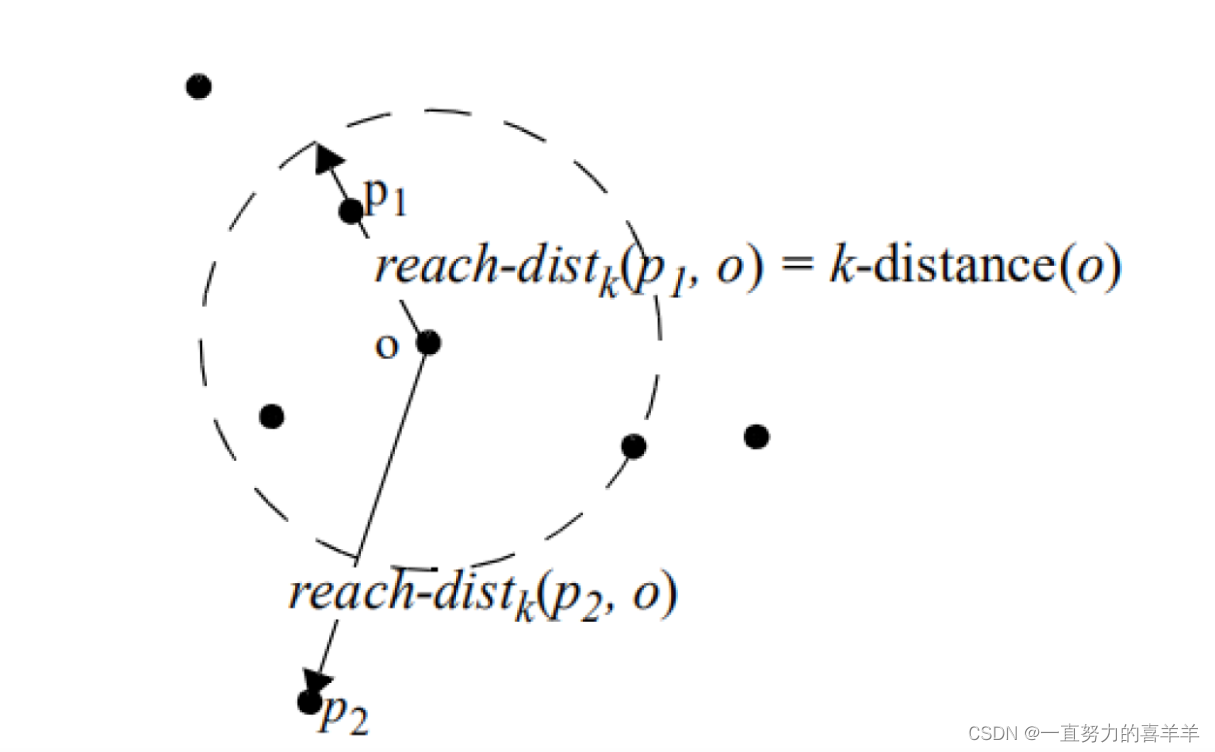
如果p点在k邻域外，那么可达距离就是真实距离，如果在k邻域内，那么就是k-距离。
局部可达密度
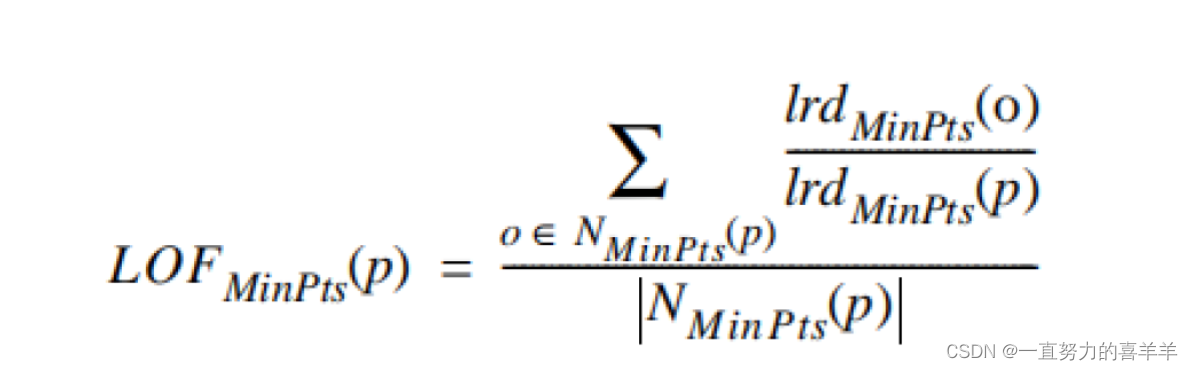
在这里插入图片描述
表示点p的邻域内其他点的局部可达密度与点p的局部可达密度之⽐的平均数。如果这个⽐值越接近1，说明o的邻域点密度差不多，o可能和邻域同属⼀簇；如果这个⽐值小于1，说明o的密度⾼于其邻域点密度，o为密集点；如果这个⽐值⼤于1，说明o的密度小于其邻域点密度，o可能是异常点。最终得出的LOF数值，就是我们所需要的离群点分数。在sklearn中有LocalOutlierFactor库，可以
直接调⽤。
参考链接：https://blog.csdn.net/qq_35692819/article/details/112973427

集成方法

集成是提高数据挖掘算法精度的常用方法。集成方法将多个算法或多个基检测器的输出结合起来。其基本思想是一些算法在某些子集上表现很好，一些算法在其他子集上表现很好，然后集成起来使得输出更加鲁棒。集成方法与基于子空间方法有着天然的相似性，子空间与不同的点集相关，而集成方法使用基检测器来探索不同维度的子集，将这些基学习器集合起来。

Feature bagging

Feature Bagging，基本思想与bagging相似，只是对象是feature。feature bagging属于集成方法的一种。集成方法的设计有以下两个主要步骤：

1.选择基检测器。这些基本检测器可以彼此完全不同，或不同的参数设置，或使用不同采样的子数据集。Feature bagging常用lof算法为基算法。
2.分数标准化和组合方法。不同检测器可能会在不同的尺度上产生分数。例如，平均k近邻检测器会输出原始距离分数，而LOF算法会输出归一化值。另外，尽管一般情况是输出较大的异常值分数，但有些检测器会输出较小的异常值分数。因此，需要将来自各种检测器的分数转换成可以有意义的组合的归一化值。分数标准化之后，还要选择一个组合函数将不同基本检测器的得分进行组合，最常见的选择包括平均和最大化组合函数。
两个feature bagging两个不同的组合分数方法：广度优先累积求和
基探测器的设计及其组合方法都取决于特定集成方法的特定目标。很多时候，我们无法得知数据的原始分布，只能通过部分数据去学习。除此以外，算法本身也可能存在一定问题使得其无法学习到数据完整的信息。这些问题造成的误差通常分为偏差和方差两种。

方差：是指算法输出结果与算法输出期望之间的误差，描述模型的离散程度，数据波动性。
偏差：是指预测值与真实值之间的差距。即使在离群点检测问题中没有可用的基本真值。

IForest

2008 ICDM 最佳论文
iForest （Isolation Forest）孤立森林是一个基于Ensemble的快速异常检测方法，具有线性时间复杂度和高精准度，是符合大数据处理要求的state-of-the-art算法。iForest 适用与连续数据（Continuous numerical data）的异常检测，将异常定义为“容易被孤立的离群点 (more likely to be separated)”——可以理解为分布稀疏且离密度高的群体较远的点。iForest属于Non-parametric和unsupervised的方法，即不用定义数学模型也不需要有标记的训练。
孤立森林假设我们用一个随机超平面来切割数据空间，切一次可以生成两个子空间。然后我们继续用随机超平面来切割每个子空间并循环，直到每个子空间只有一个数据点为止。直观上来讲，那些具有高密度的簇需要被切很多次才会将其分离，而那些低密度的点很快就被单独分配到一个子空间了。孤立森林认为这些很快被孤立的点就是异常点。
怎么来切这个数据空间是iForest的设计核心思想，本文仅介绍最基本的方法。由于切割是随机的，所以需要用ensemble的方法来得到一个收敛值（蒙特卡洛方法），即反复从头开始切，然后平均每次切的结果。iForest 由t个iTree（Isolation Tree）孤立树组成，每个iTree是一个二叉树结构，其实现步骤如下：

从训练数据中随机选择Ψ个点样本点作为subsample，放入树的根节点。
随机指定一个维度（attribute），在当前节点数据中随机产生一个切割点p——切割点产生于当前节点数据中指定维度的最大值和最小值之间。
以此切割点生成了一个超平面，然后将当前节点数据空间划分为2个子空间：把指定维度里小于p的数据放在当前节点的左孩子，把大于等于p的数据放在当前节点的右孩子。
在孩子节点中递归步骤2和3，不断构造新的孩子节点，直到孩子节点中只有一个数据（无法再继续切割）或孩子节点已到达限定高度。

获得t个iTree之后，iForest 训练就结束，然后我们可以用生成的iForest来评估测试数据了。对于一个训练数据x，我们令其遍历每一棵iTree，然后计算x最终落在每个树第几层（x在树的高度）。然后我们可以得出x在每棵树的高度平均值，即 the average path length over t iTrees。获得每个测试数据的average path length后，我们可以设置一个阈值（边界值），average path length 低于此阈值的测试数据即为异常。也就是说 “iForest identifies anomalies as instances having the shortest average path lengths in a dataset ”(异常在这些树中只有很短的平均高度). *值得注意的是，论文中对树的高度做了归一化，并得出一个0到1的数值，即越短的高度越接近1（异常的可能性越高）。
iForest算法默认参数设置如下：subsample size: 256 ;Tree height： 8;Number of trees: 100
通俗解释就是——建100棵iTree，每棵iTree最高8层，且每棵iTree都是独立随机选择256个数据样本建成。
优缺点：

iForest具有线性时间复杂度。因为是ensemble的方法，所以可以用在含有海量数据的数据集上面。通常树的数量越多，算法越稳定。由于每棵树都是互相独立生成的，因此可以部署在大规模分布式系统上来加速运算。
iForest不适用于特别高维的数据。由于每次切数据空间都是随机选取一个维度，建完树后仍然有大量的维度信息没有被使用，导致算法可靠性降低。高维空间还可能存在大量噪音维度或无关维度（irrelevant attributes），影响树的构建。对这类数据，建议使用子空间异常检测（Subspace Anomaly Detection）技术。此外，切割平面默认是axis-parallel的，也可以随机生成各种角度的切割平面，详见“On Detecting Clustered Anomalies Using SCiForest”。
iForest仅对Global Anomaly 敏感，即全局稀疏点敏感，不擅长处理局部的相对稀疏点（Local Anomaly）。目前已有改进方法发表于Computational Intelligence，详见“Isolation‐based anomaly detection using nearest‐neighbor ensembles”。
iForest推动了重心估计（Mass Estimation）理论发展，目前在分类聚类和异常检测中都取得显著效果，发表于各大顶级数据挖掘会议和期刊（如SIGKDD，ICDM，ECML）。

参考链接：https://www.jianshu.com/p/5af3c66e0410
参考链接：https://blog.csdn.net/qq_43720646/article/details/112603310

INNE

孤立森林在数值型数据上面临4大问题：

iForest仅对Global Anomaly 敏感，即全局稀疏点敏感，不擅长处理局部的相对稀疏点（Local Anomaly）。
iForest不适用于特别高维的数据。由于每次切数据空间都是随机选取一个维度，建完树后仍然有大量的维度信息没有被使用，导致算法可靠性降低。
iForest不善于找到和坐标轴平行的簇中的异常。这是因为每次建子树的时候都是按坐单个标轴进行分割，异常可能会藏在某个维度中数据分布比较密的地方。
iForest不适用于含有多个高密度分布区域的数据

为了解决以上问题，我们仍然借鉴数据数据孤立机制，并结合最近邻距离计算方法，开发出了算法iNNE (Isolation‐based anomaly detection using nearest‐neighbor ensembles)。该算法采用多维超球体切割数据空间来实现孤立机制，并考虑了数据局部分布特性即使用最近邻的距离比率来计算数据的异常指标。
从训练数据中随机选择Ψ个点样本点作为subsample，然后每个样本点都各自找到自己在其他（Ψ-1）个点样本点中离自己最近的点（俗称最近邻），以到该最近邻的距离为半径，自己为圆心画出Ψ个超球。
因为数据分布越密的地方取得的样本点也越多，所以这种以样本点画球的方法可以理解为，数据空间中数据点越密的地方画的球会越多而且体积越小，数据分布越稀疏的地方球越少且体积越大，也就是说半径越大的超球越容易被孤立。
从训练数据中随机选择Ψ个点样本点继续按步骤1画超球，重复该步骤 t 次直到我们最后可以得到 t 组超球。每次样本点都是独立从所有原始数据中随机抽样产生。
当把一个测试数据放进一组超球中的时候，评估过程如下：
5. 如果该测试数据不在任何一个超球的覆盖范围，那该测试数据的异常值就是1，直接当做孤立点了。
6. 如果该测试数据在某个超球Q的覆盖范围，首先记录超球Q的半径为q，之后再找到离超球Q最近的超球P，记录其半径为p，这个测试数据的异常值为 1 - p/q。

按照该规则，把测试数据分别放进每组超球中进行评估，得出 t 个异常值，然后用他们的平均值做为最后的异常指标。其实异常值就是两个最近超球的半径比值组成，也就是俩个最近邻距离的比值。如果测试数据在某个大半径的超球内，且附近超球半径都比较小，则越容易被孤立，因此异常值也就高了。简而言之，该方法可以把局部密度分布比较稀疏的数据点找出来当做异常。iNNE都可以把这些球的边缘赋予更高的异常值,因此iNNE可以有效的克服iForest无法查找局部异常的缺陷。

参考链接：https://www.jianshu.com/p/379a5898beb6