前言
对卷积网络进行放大可以获得更好的精度,但这一过程还未被完全理解,目前通用的几种方式是放大卷积网络的深度、宽度和分辨率,并且通常只放大这三个维度中的一种。虽然任意放大两个或三个维度也是可行的,但这需要繁琐的人工调参,并且可能不能达到最优的精度和效率。
本文研究了放大卷积网络这一过程,关注了一个核心问题:是否存在一个原则性的方法来放大卷积网络,从而能够达到更好的精度和效率? 本文的实验表明平衡网络的深度、宽度和分辨率这三个维度是非常重要的,并且仅用一组常量比率分别对每个维度进行缩放,就能实现这样的平衡。基于此,本文提出一种简单高效的复合缩放方法,使用一组固定的缩放系数来对网络的深度、宽度和分辨率进行统一缩放。下图说明了本文的缩放方法与传统方法之间的不同,(a)是基础网络,(b)-(d)是传统缩放方法,仅缩放一个维度,(e)是本文的复合缩放方法。
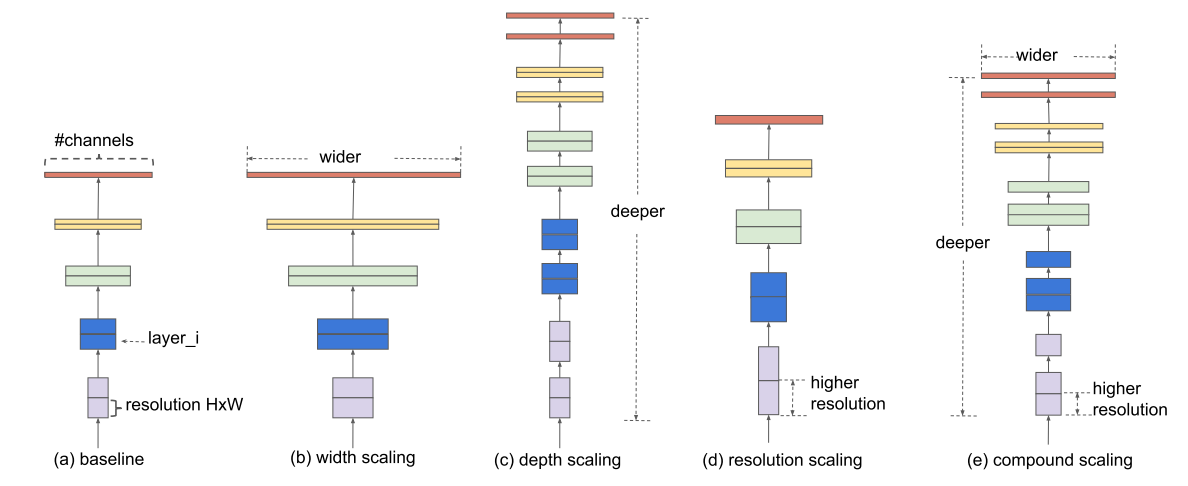
作者认为这种复合缩放方法是有用的,因为如果输入图像较大,那么网络需要更多的层(深度)以增大感受野,需要更多通道(宽度)以捕获更多细粒度信息。之前的一些工作证明网络的深度和宽度之间存在一定的关系,而本文对网络的深度、宽度和分辨率这三个维度之间的关系进行了量化。
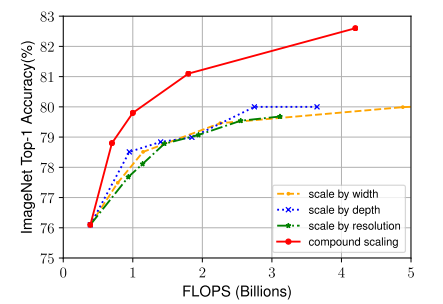
本文的复合缩放方法严重依赖于基础网络,因此为了进一步的提升,本文还使用神经架构搜索(NAS)找出了一种新的基础网络,并在此基础上进行放大,以获得一系列模型,称为EfficientNets,下图总结了不同模型在ImageNet上的表现,可以看到EfficientNets优于其它卷积网络:
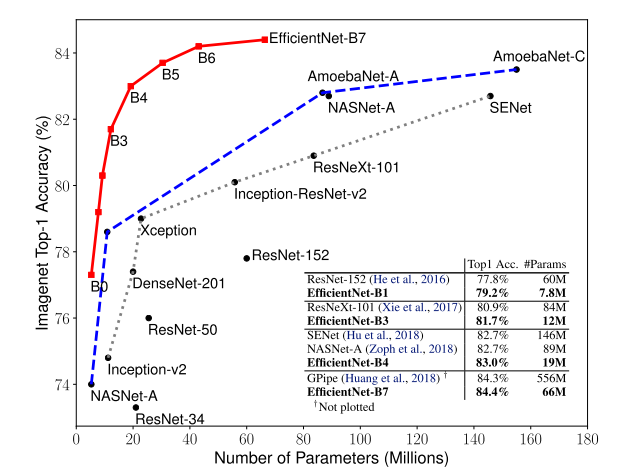
复合缩放方法
1. 问题描述
卷积层
i
i
i可以用函数描述为:
Y
i
=
F
i
(
X
i
)
Y_i=F_i(X_i)
Yi=Fi(Xi),
F
i
F_i
Fi是卷积操作,
Y
i
Y_i
Yi是输出张量,
X
i
X_i
Xi是输入张量,形状为
<
H
i
,
W
i
,
C
i
>
<H_i,W_i,C_i>
<Hi,Wi,Ci>,
H
i
H_i
Hi和
W
i
W_i
Wi是特征图的尺度,
C
i
C_i
Ci是特征图的输入通道数。那么卷积网络
N
N
N可以表示为:
N
=
F
k
⨀
.
.
.
⨀
F
2
⨀
F
1
(
X
1
)
=
⨀
j
=
1...
k
F
j
(
X
1
)
N=F_k bigodot ... bigodot F_2 bigodot F_1(X_1)= bigodot_{j=1...k}F_j(X_1)
N=Fk⨀...⨀F2⨀F1(X1)=⨀j=1...kFj(X1)。而在实际中,卷积层通常会被划分为多个stage,并且每个stage中的所有层共享相同的结构。那么,卷积网络可以被定义为:
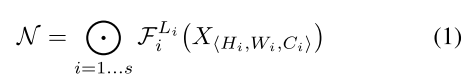
F
i
L
i
F_i^{L_i}
FiLi表示在stage
i
i
i中,卷积层
F
i
F_i
Fi重复了
L
i
L_i
Li次。从下图中可以看出,在典型的卷积网络中,其空间维度,也就是特征图的尺度会逐渐减小,而通道维数是逐层增加的。
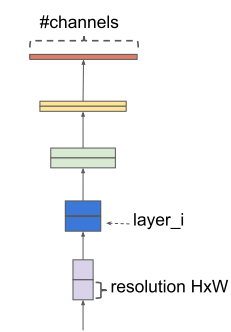
常规的卷积网络设计大多数关注如何才能使层结构
F
i
F_i
Fi达到最好,而模型的缩放是在不改变基础网络中
F
i
F_i
Fi的预设结构的情况下,试着扩展网络的深度(
L
i
L_i
Li),宽度(
C
i
C_i
Ci)和分辨率(
H
i
,
W
i
H_i,W_i
Hi,Wi)。通过固定
F
i
F_i
Fi,可以简化设计问题,但对于每层的
L
i
,
C
i
,
H
i
,
W
i
L_i,C_i,H_i,W_i
Li,Ci,Hi,Wi来说,仍然有很大的设计空间。因此,为了进一步减小设计空间,要对所有层施加一个限制,即所有层必须以一定的常量比例进行统一缩放。 那么我们的目标就是在给定任意资源预算的情况下,最大化模型的精度,也就是说变成了一个优化问题:
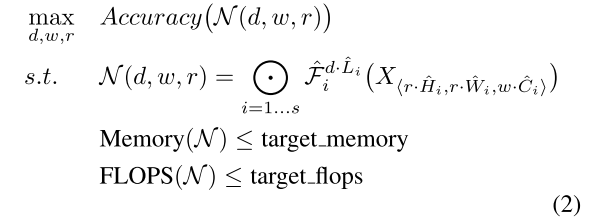
w
,
d
,
r
w,d,r
w,d,r分别是缩放网络的宽度、深度和分辨率时的系数,
F
i
^
,
L
i
^
,
H
i
^
,
W
i
^
,
C
i
^
hat{F_i},hat{L_i},hat{H_i},hat{W_i},hat{C_i}
Fi^,Li^,Hi^,Wi^,Ci^是基础网络中预设的参数。
2. 对三种维度分别进行缩放
下面说一下只缩放深度、宽度和分辨率其中的一个维度,会带来什么结果:
深度( d d d):
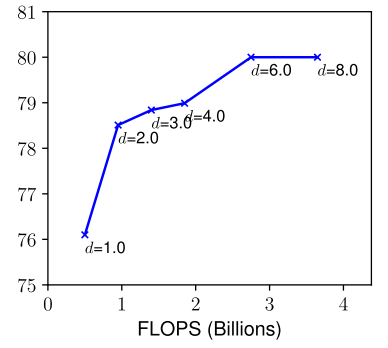
对深度进行缩放是一种最常用的方式,因为通常来说更深的网络能够捕获更丰富且更复杂的特征。但是,由于随着网络深度的增大,梯度会逐渐消失,因此更深的网络也更难训练。虽然跳层连接、批归一化等可以有效缓解训练问题,但在很深的网络中,精度的提升是非常有限的。比如ResNet-1000和ResNet-101的精度是相似的,虽然前者有更多的层。下图说明了使用不同深度系数
d
d
d来缩放基础网络的研究结果,进一步表明在非常深的卷积网络中,精度回报会逐渐减弱。
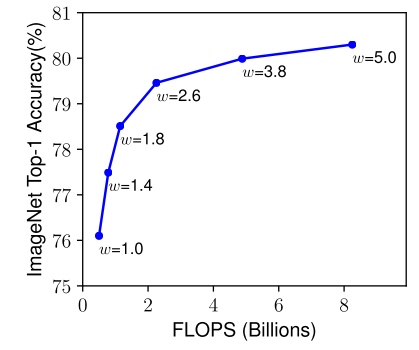
宽度( w w w):
缩放网络的宽度常用于一些较小的模型中,更宽的网络能够捕获更多细粒度特征,并且易于训练。但是,如果网络极宽,但是却很浅,那么在捕获高层级特征时是很困难的。本文的实验结果也说明了当网络宽度随着
w
w
w变大时,精度很快就饱和了。
分辨率( r r r):
输入图像的分辨率越高,卷积网络越能捕获到更多的细粒度信息。早期卷积网络使用
224
×
224
224 times 224
224×224的输入,现在有些卷积网络为了获得更好的精度,使用
299
×
299
299 times 299
299×299或
331
×
331
331 times 331
331×331作为输入。目前
600
×
600
600 times 600
600×600也被广泛使用在目标检测网络中。下图说明了缩放网络分辨率的结果,更高的分辨率确实能够提升精度,但同样在非常高的分辨率时网络的精度回报会减弱。
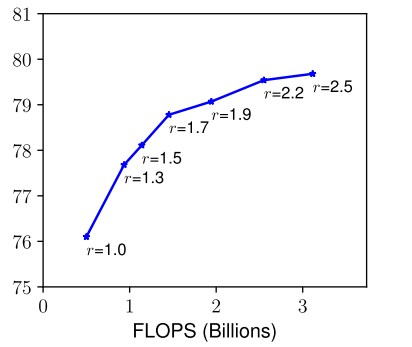
基于以上分析,可以得到observation 1:对网络的宽度、深度和分辨率中的任何一个维度进行放大都能够提升网络精度,但当模型足够大时,精度的收益会减弱,也就是精度会逐渐趋于饱和。
3. 复合缩放
通过上面的实验可以观察到不同的缩放维度之间其实是有一定关系的,比如对于更高分辨率的图像来说,应该增加网络的深度,从而能有更大的感受野,有助于捕获更多像素点间的相似特征;与此同时也应该增大网络的宽度以捕获更多细粒度特征。也就是说协调平衡不同的缩放维度,比单一维度的缩放更重要。
为了验证这一点,本文在不同的网络深度和分辨率下比较了宽度变化的影响,如下图所示。可以看到,如果只缩放宽度而不去改变深度和分辨率(
d
=
1.0
,
r
=
1.0
d=1.0,r=1.0
d=1.0,r=1.0),那么精度很快就饱和了(蓝线)。而在更深(
d
=
2.0
d=2.0
d=2.0)和更高分辨率(
r
=
1.3
r=1.3
r=1.3)的情况下,缩放宽度可以得到更好的精度,并且FLOPS与之前相比是相同的(红线)。
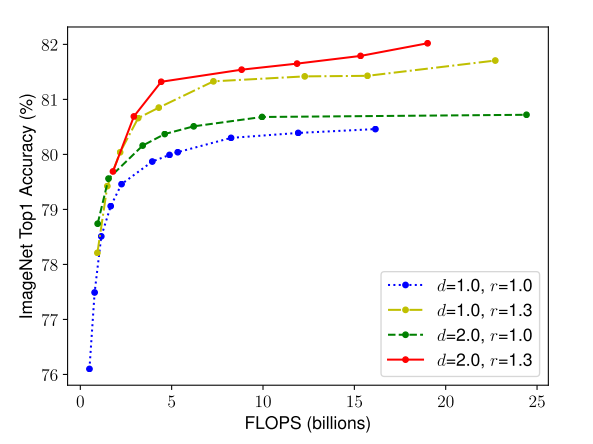
基于此,可以得到observation 2:为了获得更好的精度和效率,在缩放过程中平衡网络的所有维度是至关重要的。
虽然之前的一些工作已经试着去平衡网络的深度和宽度,但这些方法都需要繁琐的人工调参。本文提出了一种新的复合缩放方法,使用复合系数
ϕ
phi
ϕ对网络的深度、宽度和分辨率进行统一缩放:
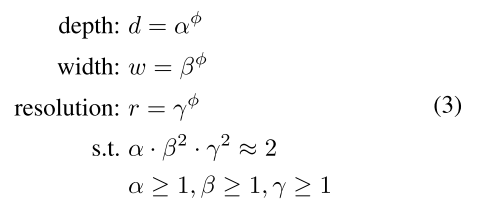
α
,
β
,
γ
alpha , beta , gamma
α,β,γ是常量,可以通过small grid search得到。直观上来看,
ϕ
phi
ϕ是一个特定的系数,用于控制模型缩放所能使用的资源数量;而
α
,
β
,
γ
alpha , beta , gamma
α,β,γ决定了如何将这些资源分别分配给网络的深度、宽度和分辨率。常规的卷积op计算量(FLOPS)是和
d
,
w
2
,
r
2
d,w^2,r^2
d,w2,r2成正比的,深度加倍会使得FLOPS加倍,而宽度和分辨率加倍会使得FLOPS变为原来的4倍。由于卷积ops通常占据了卷积网络大部分的计算,因此使用式(3)对卷积网络进行缩放将会使得整体FLOPS近似增加
(
α
⋅
β
⋅
γ
)
ϕ
(alpha cdot beta cdot gamma)^{phi}
(α⋅β⋅γ)ϕ倍。本文施加约束为
α
⋅
β
2
⋅
γ
2
≈
2
alpha cdot beta^2 cdot gamma^2 approx 2
α⋅β2⋅γ2≈2,因此对于任意
ϕ
phi
ϕ,整体的FLOPS近似增加
2
ϕ
2^{phi}
2ϕ倍。
4. EfficientNet的结构
由于模型的尺度变化并不会改变基础网络中卷积操作 F i ^ hat{F_i} Fi^,因此有一个好的基础网络是很重要的。受MansNet的启发,本文利用多目标神经架构搜索找出一种新的基础网络,同时对精度和FLOPS进行优化。本文使用的搜索空间与MansNet相同,优化目标为 A C C ( m ) × [ F L O P S ( m ) / T ] w ACC(m) times [FLOPS(m)/T]^w ACC(m)×[FLOPS(m)/T]w, A C C ( m ) ACC(m) ACC(m)和 F L O P S ( m ) FLOPS(m) FLOPS(m)分别表示模型 m m m的精度和FLOPS, T T T是目标FLOPS, w = − 0.07 w=-0.07 w=−0.07是一个超参数,用于控制精度和FLOPS之间的trade-off。与MansNet中的优化目标不同,这里优化的是FLOP而不是延迟,因为本文并没有说在某个特定的硬件平台上做加速。
通过搜索可以产生一个高效的网络,称为EfficientNet-B0,它和MnasNet的结构是相似的,但是由于FLOPS预算比MnasNet中大,因此EfficientNet-B0也稍微大了点。下标说明了EfficientNet-B0的结构,它主要由mobil inverted bottleneck MBConv组成,也添加了squeeze-and-excitation操作:
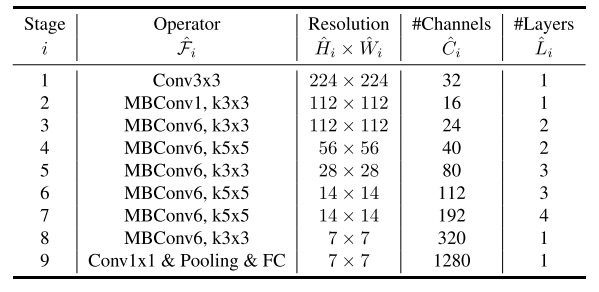
从基础网络EfficientNet-B0开始,对其应用复合缩放方法以进行放大,主要有两个步骤:
- 第一步:固定 ϕ = 1 phi=1 ϕ=1,假设有相当于原来两倍的资源可以用,基于式(2)和(3)对 α , β , γ alpha,beta,gamma α,β,γ做small grid search,然后发现,对于EfficientNet-B0来说最优值为 α = 1.2 , β = 1.1 , γ = 1.15 alpha=1.2,beta=1.1,gamma=1.15 α=1.2,β=1.1,γ=1.15,当然要在 α ⋅ β 2 ⋅ γ 2 ≈ 2 alpha cdot beta^2 cdot gamma^2 approx 2 α⋅β2⋅γ2≈2这一约束下进行;
- 第二步:然后固定
α
,
β
,
γ
alpha,beta,gamma
α,β,γ作为常量,使用式(3)来利用不同的
ϕ
phi
ϕ值对基础网络进行放大,获得Efficient-B1到B7,如下表所示:
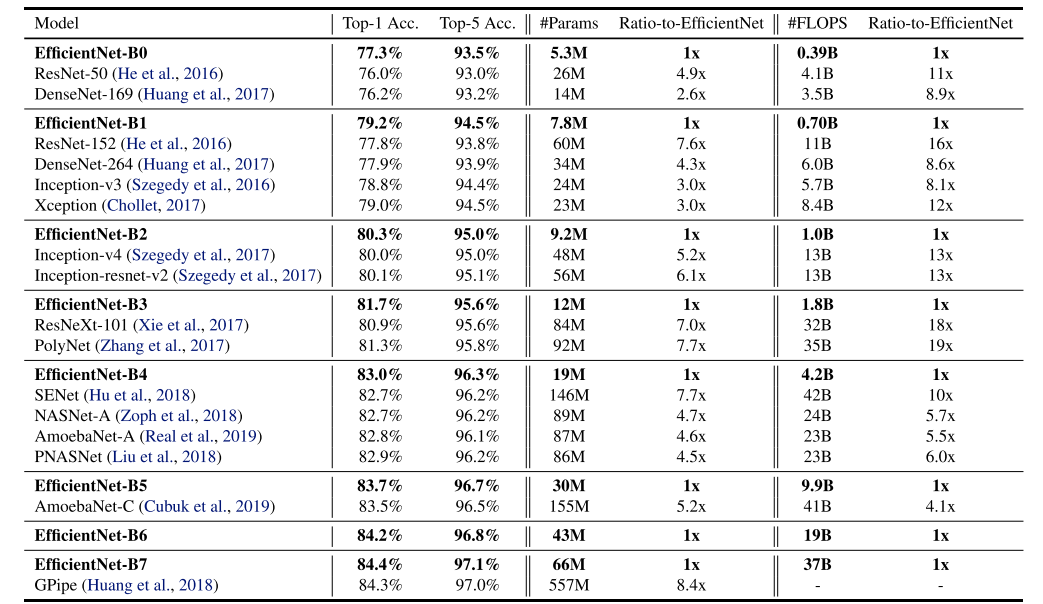
虽然直接在一个大型模型上搜索 α , β , γ alpha,beta,gamma α,β,γ可能会达到更好的性能,但这样的话搜索成本会很高。本文的方法解决了这个问题,即仅在较小的基础网络上做了一次搜索得到 α , β , γ alpha,beta,gamma α,β,γ(第一步),然后通过变换 ϕ phi ϕ的大小来调整模型(第二步)。
讨论
为了说明本文提出的复合缩放方法的作用,下表比较了不同缩放方法在EfficientNet-B0上的ImageNet的性能,可以看到所有的缩放方法都能提高精度,FLOPS的成本也更多,但复合缩放方法能够进一步提升精度,大概有2.5%
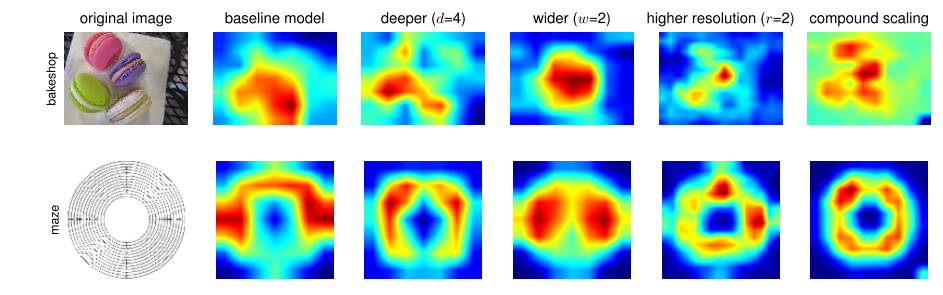
为了进一步说明为什么本文的复合缩放方法比其它的方法好,下图比较了使用不同缩放方法的模型得到的class activation map,所有的模型都是在相同的基础网络上进行缩放得到的,原始图像是从ImageNet验证集中随机得到的。可以看到,使用复合缩放方法的模型更关注与更多目标细节相关的区域,而其他的模型要么缺少目标细节,要么无法捕获图像中的所有目标。
结论
本文对网络的三个维度:宽度、深度和分辨率进行统一缩放,提出一种复合缩放方法,同时为了让这种方法发挥更好的作用,还利用神经架构搜索找出一种新的基础网络EfficientNet,在这个网络的基础上利用复合缩放方法得到了一系列高效的网络。
最后
以上就是狂野钥匙最近收集整理的关于EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks 论文笔记前言复合缩放方法讨论结论的全部内容,更多相关EfficientNet:内容请搜索靠谱客的其他文章。








发表评论 取消回复