目录
- 多智能体编队基本分类
- 多智能体编队的其他分类方式
- 基于位置的编队控制:
- 基于位移的编队控制
- 基于距离的编队控制
- 基于无向图的双积分模型:
多智能体编队基本分类
基于位置的编队控制:智能体感知自己相对于全局坐标系的位置。它们主动控制自己的位置,以实现所需的队形,这是由相对于全局坐标系的所需位置规定的。
基于位移的编队控制:智能体主动控制其相邻智能体的位移以实现所需的队形,这个队形是在假设每个智能体能够感知其相邻智能体相对于全局坐标系的相对位置的情况下,由相对于全局坐标系的期望位移指定的。这意味着智能体只需要知道全局坐标系的方向,既不需要全局坐标系本身的信息,也不需要它们相对于坐标系的位置。
基于距离的编队控制:主动控制智能体间距离,以实现所需的编队,这是由所需的智能体间距离给出的。假设单个智能体能够感知其相邻智能体相对于其本地坐标系的相对位置。局部坐标系的方向不一定相互对齐。
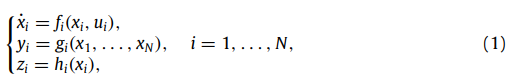
xi表示状态量,yi表示系统的测量量,zi表示观测量,ui表示控制量
一般的编队控制问题:通过仅使用测量值yi设计控制律,使得系统的观测值等于期望观测值,即使多智能体系统是渐近稳定的。
通过仅使用测量值设计控制律,使得:
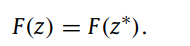
我们在以下方面描述了基于位置、位移和距离的编队控制问题:
基于位置的问题:测量值包含一些相对于全局坐标系感测的绝对变量。智能体直接控制zi 即F(z) = z;
基于位移的问题:测量值包含相对于全局坐标系感测的相关变量。但是,它们不包含任何需要相对于全球坐标系进行检测的绝对变量。智能体控制 (zi - zj),对于平移不变。即F(z) = […(zi - zj)… ] =F(z*)
基于距离的问题:在基于距离的控制问题中,测量值仅包含相对于智能体的局部坐标系可感测的相对变量。它们不包含任何需要相对于全局坐标系感测的绝对和相对变量。智能体控制 ||zi - zj||,对平移,旋转不变。即F(z) = […||zi - zj||… ] =F(z*)
我们注意到,一致性通常可以被视为一种特殊的编队控制,如期望的z* =0,F(z) = […(zi - zj)… ]
多智能体编队的其他分类方式
根据队形是否随时间变化,分为①编队产生问题:即智能体达到规定的队形;②编队跟踪问题:规定了智能体的参考轨迹,并控制智能体跟踪轨迹。
根据控制方案的基本思想,将编队控制分为①领导者-追随者:至少有一个智能体扮演领导者的角色,其余智能体被指定为追随者。领导者跟踪它的期望轨迹时,跟随者跟踪满足一定条件后的领导者的位置。②行为方法:在这种方法中,为智能体规定了几种期望的行为。此类预期行为可能包括内聚、避碰、避障等。③虚拟结构方法:队形的形成由虚拟结构确定。给出了虚拟结构的期望运动。智能体所需的运动由虚拟结构的运动确定。
根据是否明确规定了所需的编队形状,分为①固定编队控制:所需队形由所需智能体位置、所需智能体间位移、所需智能体间距离等明确规定。②无定形编队控制:在没有明确规定的预期编队的情况下,为代理提供了期望的行为,如内聚、避免碰撞等。无定形形成控制与上述行为方法有关。
基于位置的编队控制:
•感知能力:智能体通常需要有一个全局坐标系。它们需要感知它们相对于全局坐标系的绝对位置。
•交互拓扑:所需的队形由智能体的所需绝对位置指定。在这种情况下,不一定需要交互,因为所需的队形可以通过单个智能体的位置控制来实现。在基于位置的控制中,可以引入智能体之间的交互,以提高控制性能或实现其他目标,如保持队形。
研究方向:①引入智能体之间的交互来提高编队控制的性能。这种交互结果是有益的。②引入一个全局协调器,从智能体获取反馈,并为智能体提供适当的协调命令。如理的驱动能力有限或受到干扰,这种反馈协调是有益的。
例子:
单积分模型: p’i = ui (i=1,2,3,…) 已知p*,定义ep=p*-p;①定义ep的导数为-Kpep;故控制量u = Kpep;在这种控制量下,ep是以指数级趋近0;②定义ep的导数为-Kpep - (L⊗In)ep;故控制量u = Kpep + (L⊗In)ep;在这种控制量下,ep是以指数级趋近0;其中L是拉普拉斯矩阵,若L中的特征值都大于等于0(即图包含生成树),则上述控制时有益的。 (Kp>0)
双积分模型; p’'i = ui (i=1,2,3,…) 已知p*,定义ep=p*-p;定义ep的二阶导为 −Ka(Kvep + Kpep) − (L ⊗ In)(Kvep + Kpep);故控制量u = Ka(Kvep + Kpep) + (L ⊗ In)(Kvep + Kpep) ; (Ka,Kp,Kv都大于0)
基于位移的编队控制
•传感能力:要求智能体拥有自己的本地坐标系,其方向与全局坐标系的方向一致。然而,他们不必知道全局坐标系的原点。对于局部坐标系,代理需要感知其邻居相对于全局坐标系的相对位置(位移),这意味着交互的存在。注意,由于坐标系对齐,相对于局部坐标系的相对位置与相对于全局坐标系的相对位置相同。
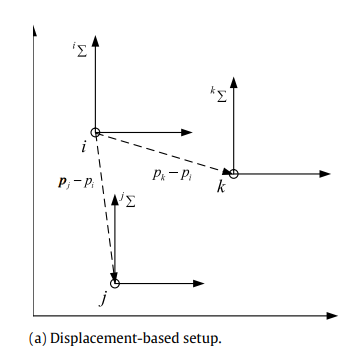
•交互拓扑:智能体的期望队形由从任何智能体到其他智能体的期望位移指定。为了达到预期的队形,智能体主动控制其邻居的位移。因此,交互图需要通过仅控制其邻域的位移来确保实现所需的队形,它可以用生成树的连通性或存在性来表征。在交互图的边是时变的情况下,一致连通性刻画了图的条件。
单积分模型: p’i = ui (i=1,2,3,…) 已知p*,定义ep=p*-p;①定义ep的导数为 - Kp(L⊗ In)ep;故控制量u= Kp(L⊗ In)ep
双积分模型; 如下:
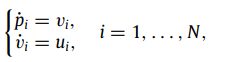
选择控制量如下:
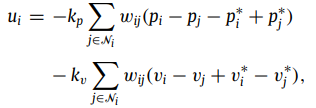
定义ep=p*-p,定义ep的导数满足如下等式:
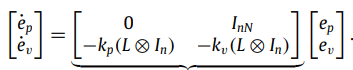
线性模型:

假设只有少数智能体能够感知其绝对位置。与基于位置的控制不同,假设此类智能体的数量远小于代理的总数。

基于距离的编队控制
•感应能力:智能体需要有自己的机体坐标系。坐标系的方向不需要彼此对齐。此外,智能体不需要有共同的方向感。要求智能体感知其邻居的相对位置,这意味着代理之间存在交互。
•交互拓扑:任何一对智能体之间的期望距离指定了期望的队形。也就是说,可以将所需的形状视为给定的刚体。因此,所需的队形对于应用于相应位置的平移和旋转的组合是不变的。为了通过控制智能体之间的距离来实现期望位置,交互图需要是刚性的或持久的,
在基于距离的控制中,即使智能体模型是线性的,控制律也是非线性的。此外,在基于距离的控制律下分析多智能体系统的不变集具有挑战性。这些事实使基于距离的编队控制复杂化。在下文中,我们将回顾无向和定向编队的基于距离的控制。
基于无向图:单积分模型



改进:

基于无向图的双积分模型:
模型如下:
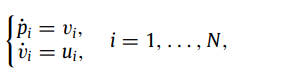
控制量: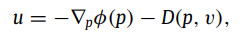
其中:
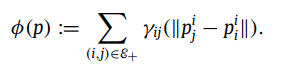
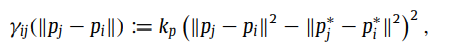
D(p,v) 满足如下:
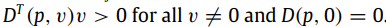
证明在:Olfati-Saber, R., & Murray, R.M. (2002). Distributed cooperative control of multiple
vehicle formations using structural potential functions. In Proceedings of the
15th IFAC world congress (pp. 346–352).
改进:
定义
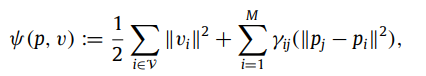
则可以得到:

基于距离的有向图的编队控制
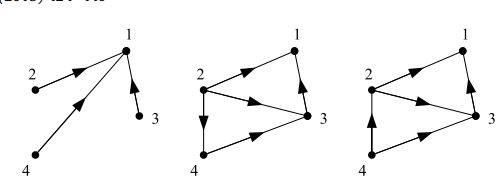
下图表明了基于距离的控制在编队上对有向图的要求,图1是非刚性的,编队是绝对无法完成的,图3相比于图2,每个节点的任务量都比较小。
最后
以上就是无限香氛最近收集整理的关于论文:多智能体编队控制综述多智能体编队基本分类多智能体编队的其他分类方式基于位置的编队控制:基于位移的编队控制基于距离的编队控制基于无向图的双积分模型:的全部内容,更多相关论文:多智能体编队控制综述多智能体编队基本分类多智能体编队内容请搜索靠谱客的其他文章。








发表评论 取消回复