刷题：《七月在线》机器学习笔试部分（一）

87 阅读 0 评论 58 点赞

我是靠谱客的博主孝顺烤鸡，最近开发中收集的这篇文章主要介绍刷题：《七月在线》机器学习笔试部分（一），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1. 以下哪种方法属于判别式模型(discriminative model)（D ）

A：隐马模型(HMM)；B：朴素贝叶斯；C：LDA；D：支持向量机

解：

判别式模型（Discriminative Model）是直接对条件概率p(y|x;θ)建模。常见的判别式模型有线性回归模型、线性判别分析、支持向量机SVM、神经网络等。

　　生成式模型（Generative Model）则会对x和y的联合分布p(x,y)建模，然后通过贝叶斯公式来求得p(yi|x)，然后选取使得p(yi|x)最大的yi，即：

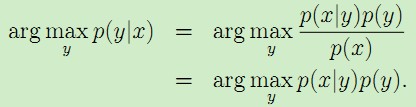
常见的生成式模型有隐马尔可夫模型HMM、朴素贝叶斯模型、高斯混合模型GMM、LDA等。

2.如下表是用户是否使用某产品的调查结果（）请计算年龄、地区、学历、收入中对用户是否使用调查产品信息增益最大的属性。（）

A：年龄；B：地区；C：学历；D：收入

解：信息增益最大，也就是分类以后信息最少，熵最小。没有划分时，原始数据熵为，如果按照年龄进行划分，划分后的熵为，分别按照熵的方法计算出划分以后的熵值，可以发现按照学历划分以后，熵为0，其他选项都大于0。因此，信息增益最大的属性是学历。

https://blog.csdn.net/u011956147/article/details/78967145

3.如果线性回归模型中的随机误差存在异方差性，那么参数的OLS估计量是（）

A 无偏的，有效的；B无偏的，非有效的；C 有偏的，有效的；D 有偏的，非有效的

解：OLS最小二乘法，通常用于线性回归模型。在满足回归假设的前提下，是具有最小方差的线性无偏估计量。随机误差中存在异方差性不会影响其无偏性，而有效性证明中涉及同方差性，即异方差会影响参数OLS估计量的有效性。对于同方差和异方差的理解：随机误差项具有相同的方差，则称线性回归模型存在同方差性。　随机误差项具有不同的方差，则称线性回归模型存在异方差。

4. 在其它条件不变的前提下，以下哪种做法容易引起机器学习中的过拟合问题（）

A增加训练集数量；B 减少神经网络隐藏层节点数；C删除稀疏的特征；D SVM算法中使用高斯核/RBF核代替

解：由此对应的降低过拟合的方法有：（1）简化模型假设，或者使用惩罚项限制模型复杂度；（2）进行数据清洗，减少噪声；（3）收集更多训练数据。

A属于增加训练数据；B属于简化模型，C属于数据清洗，而D是增加了模型的复杂度，更容易过拟合。

5.下面关于ID3算法中说法错误的是（）

AID3算法要求特征必须离散化；B信息增益可以用熵，而不是GINI系数来计算；C选取信息增益最大的特征，作为树的根节点

D ID3算法是一个二叉树模型

解：ID3算法（IterativeDichotomiser3迭代二叉树3代）是一个由RossQuinlan发明的用于决策树的算法。可以归纳为以下几点：使用所有没有使用的属性并计算与之相关的样本熵值选取其中熵值最小的属性生成包含该属性的节点。D3算法对数据的要求： 1)所有属性必须为离散量； 2)所有的训练例的所有属性必须有一个明确的值； 3)相同的因素必须得到相同的结论且训练例必须唯一。

6.在二分类问题中，当测试集的正例和负例数量不均衡时，以下评价方案哪个是相对不合理的（）（假设precision=TP/(TP+FP),recall=TP/(TP+FN)。）

A Accuracy:(TP+TN)/all；B F-value:2*recall*precision/(recall+precision)； C G-mean:sqrt(precision*recall)； D AUC:ROC曲线下面积

解：要认真学习机器学习算法中的评价指标。对于分类器，主要的评价指标有precision，recall，F-score，以及ROC曲线等。在二分类问题中，我们主要关注的是测试集的正样本能否正确分类。当样本不均衡时，比如样本中负样本数量远远多于正样本，此时如果负样本能够全部正确分类，而正样本只能部分正确分类，那么(TP+TN)可以得到很高的值，也就是Accuracy是个较大的值，但是正样本并没有取得良好的分类效果。因此A选项是不合理的。在样本不均衡时，可以采用BCD选项方法来评价。

7.隐马尔可夫模型（HMM），设其观察值空间为，状态空间为，如果用维特比算法(Viterbi algorithm)进行解码，时间复杂度为（）