毫米波Saleh-Valenzuela信道模型的array response详细推导

71 阅读 0 评论 47 点赞

我是靠谱客的博主温暖小伙，最近开发中收集的这篇文章主要介绍毫米波Saleh-Valenzuela信道模型的array response详细推导，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

在解决毫米波物理层相关问题的时候，总是不可避免地会碰到信道建模，而比较常见的毫米波信道模型就是S-V模型，在介绍信道模型之前，我们先确定天线的类型和空间位置，文献中比较常见的是线阵ULA和面阵UPA，本文侧重与UPA，天线总数是M， $m=m_{mathrm{v}} m_{mathrm{h}}$ ，天线的空间坐标系如下图所示：

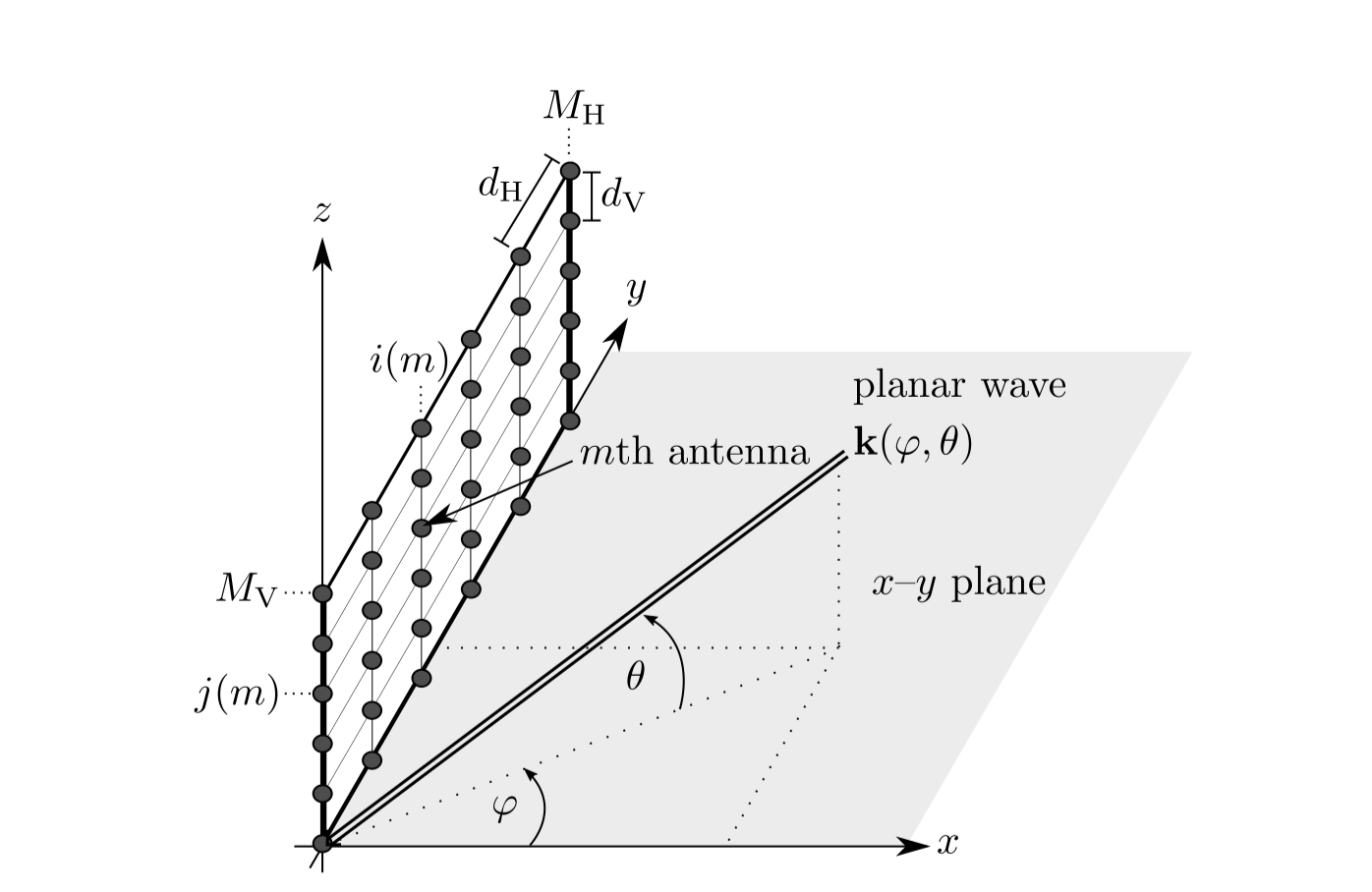
需要注意的有两点，第一，此处UPA位于yz平面，这样推导出来的array response与在其他平面的array response是不一样的，但是推导过程类似。第二，方位角 $varphi$ 和仰角 $theta$ 是如何确定的，不同的文献中可能会有不同的确定方式，在公式推导和代码过程中都是需要我们注意的。

首先，给出LOS信道的基本形式：

$mathbf{h}=sqrt{beta}left[begin{array}{ccc} e^{jmathbf{k}(varphi,theta)^{t}mathbf{u}_{1}}, & ldots, & e^{jmathbf{k}(varphi,theta)mathbf{u}_{1}}end{array}right]$ （1）

其中， $beta$ 描述了宏观的大规模衰落，并假定对于所有天线都是相同的（即阵列孔径与传播距离相比较小）；后面矩阵中就是array response，记为 $mathbf{a}(varphi,theta)$ 。

而其中的 $mathbf{k}(varphi, theta)$ 是波长为 $lambda$ 的平面波wave vector波形矢量，方位角和仰角的范围分别是 $varphi in[-pi, pi)$ ， $theta in[-pi / 2, pi / 2)$ 。

$mathbf{k}(varphi, theta)=frac{2 pi}{lambda}left[begin{array}{c} cos (theta) cos (varphi) \ cos (theta) sin (varphi) \ sin (theta) end{array}right]$ （2）

波形矢量的物理意义是描述了平面波相对于笛卡尔坐标系的相位变化，如上图所示，所以在观察点 $mathbf{u} in mathbb{r}^{3}$ 处的波wave相较于原点经历了 $mathbf{k}(varphi, theta)^{mathrm{t}} mathbf{u}$ 的相位变化。

如果我们把wave观察点的坐标表示出来， $（a,b,c）$ $(a,b,c)$ ，观察点到原点的距离为d，那么公式（2）可以改写为：

$mathbf{k}(varphi, theta)=frac{2 pi}{lambda}left[begin{array}{c} a/d \ b/d \ c /d end{array}right]$ （3）

如果天线是ULA，意味着没有仰角， $theta = 0$ ，天线是在y轴上的，天线间隔是 $d_{h}$ ，那么此时的第m个天线的位置可以表示为

$mathbf{u}_{m}=left[0, lambda(m-1) d_{mathrm{h}}, 0right]^{mathrm{t}}$ （4）

将公式（2）和（4）代入（1），array response

$mathbf{a}left(varphi,thetaright)=left[1,e^{j2pi d_{h}sin(varphi)},ldots,e^{j2pi d_{h}sin(varphi)}right]$ (5)

如果天线是UPA，位于y-z平面，天线间隔是 $d_{h}$ 和 $d_{v}$ ,那么此时的第m个天线的位置可以表示为

$mathbf{u}_{m}=left[begin{array}{c} 0 \ i(m) d_{mathrm{h}} lambda \ j(m) d_{mathrm{v}} lambda end{array}right]$ (6)

操作步骤同上，那么此时的array response可以表示为

$mathbf{a}left(varphi,thetaright)=left[1,ldots,e^{j2pi/lambda(i(m)d_{h}sin(varphi)cos(theta)+j(m)d_{v}sin(theta))},ldotsright]$ （7）

S-V信道的生成代码可以参考https://github.com/yuxianghao/Alternating-minimization-algorithms-for-hybrid-precoding-in-millimeter-wave-MIMO-systems

但是这里的代码与公式推导的部分有一些出入，因为坐标系的选取不同，所以有需求还是按照需求更改代码即可。

主要参考：Massive MIMO Networks: Spectral, Energy, and Hardware Eﬃciency, https://ebjornson.com/research/

https://blog.csdn.net/weixin_39274659/article/details/108894763?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522160612065419195264721461%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=160612065419195264721461&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_v2~rank_blog_default-1-108894763.pc_v2_rank_blog_default&utm_term=DFT&spm=1018.2118.3001.4450