matlab描述线性系统传递函数

1.连续线性系统的数学模型与MATLAB表示

1.1传递函数模型

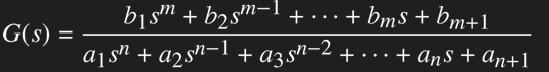
方法一：

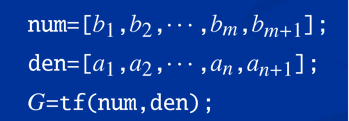
方法二：tf('s')算子

示例：

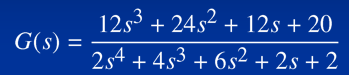
%方法一：
B=[0 12 24 12 20];A=[2 4 6 2 2];%降幂排列，注意系数对齐
G=tf(B,A)

%方法二：
s=tf('s')
G=(12*s^3+24*s^4+12*s+20)/(2*s^4+4*s^3+6*s^2+2*s+2)

1.2状态方程模型

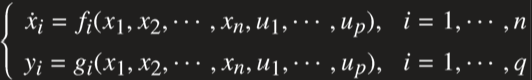
线性状态方程：

线性时不变模型的matlab描述：

G=ss(A,B,C,D）

示例：

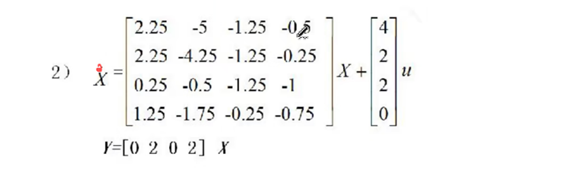
A=[2.25 -5 -1.25 -0.5;2.25 -4.25 -1.25 -0.25;0.25 -0.5 -1.25 -1;1.25 -1.75 -0.25 -0.75]
B=[4;2;2;0]
C=[0 2 0 2]
D=[]
G=ss(A,B,C,D)%D其实可以省略

1.3零极点模型

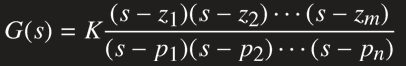
matlab表示：G=zpk(z,p,k)，pzmap(G)可以绘制零极点分布图

2.线性离散系统的数学模型

2.1离散传递函数模型

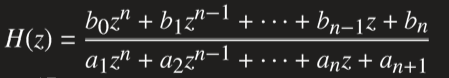
方法一：

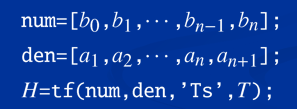
方法二：z=tf('z',T)算子输入法

2.2离散状态方程

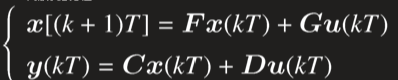
H=ss(F,G,C,D,'Ts','T')

• 离散延迟系统的状态方程

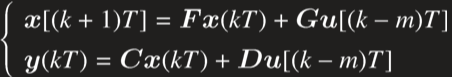
H=ss(F,G,C,D,'Ts','T','ioDelay',m)

3.方框图

3.1串并联

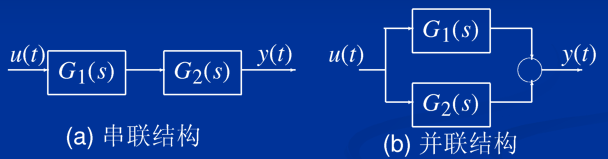
%matlab计算
G=G2*G1  %串联
G=G1+G2  %并联

3.2反馈

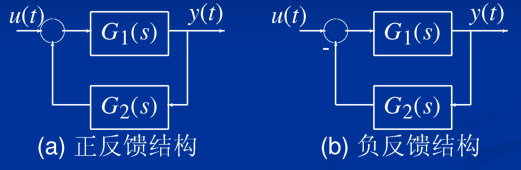
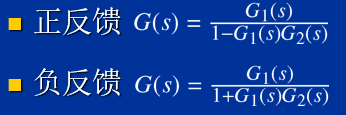
G=feedback(G1,G2)  %负反馈
G=feedback(G1,G2,1)  %正反馈

4.系统模型的相互转换

4.1连续模型和离散模型的相互转换

G1=c2d(G,T)  %连续转换为离散
G2=d2c(G)    %离散模型连续化

4.2一般传递函数与零极点模型转换

G=tf([1 3 6],[3 2 5])
Gzpk=zpk(G)   %zpk()函数可以将其他模型转换为零极点模型，同理ss()函数也可以
G1=tf(Gzpk)   %tf()函数可以将其他模型转换为一般的传递函数模型