参考

信号实验指导.pdf
信号实验三和实验四.pdf
《信号与系统》4.11.2系统函数的幅频特性和相频特性分析 MATLAB实现

第一大题

内容

设
$$H(s)=\frac{s}{(s-p1)(s-p2)}$$
设①p1= -2，p2= -30； ②p1= -2，p2=3
（1）针对极点参数①②，画出系统零、极点分布图，判断该系统稳定性。
（2）针对极点参数①②，绘出系统的脉冲响应曲线，并观察t→∞时，脉冲响应变化趋势。
（3）针对极点参数①，绘出系统的频响曲线。

题（1）画出系统零、极点分布图，判断该系统稳定性

参考方法

residue()-部分分式展开式求解函数

系统函数H(s)的部分分式展开式可用matlab的函数residue( )求得。
调用格式： [r,p,k]=residue(num,den)
式中，num和den分别为 F(s)的分子多项式和分母多项式的系数，r为部分分式的系数，p为极点，k为多项式的系数，若F(s)为真分式，则k=0。

roots()-多项式求根函数

系统函数H(s)的零、极点可用matlab的多项式求根函数roots( )求得。
极点：p=roots(den)
零点：z=roots(num)

pzmap(sys)

根据p和z用plot()命令即可画出系统零、极点分布图，进而分析判断系统稳定性。也可以调用pzmap函数，调用格式：
pzmap(sys),
其中sys借助tf函数获得：sys=tf(b,a)，表示sys的系统转移函数以b为分子多项式系数、a为分母多项式系数。

impulse(num,den,T)-脉冲响应

脉冲响应可调用impulse求得：
y=impulse(num,den,T)
T：为等间隔的时间向量，指明要计算响应的时间点。

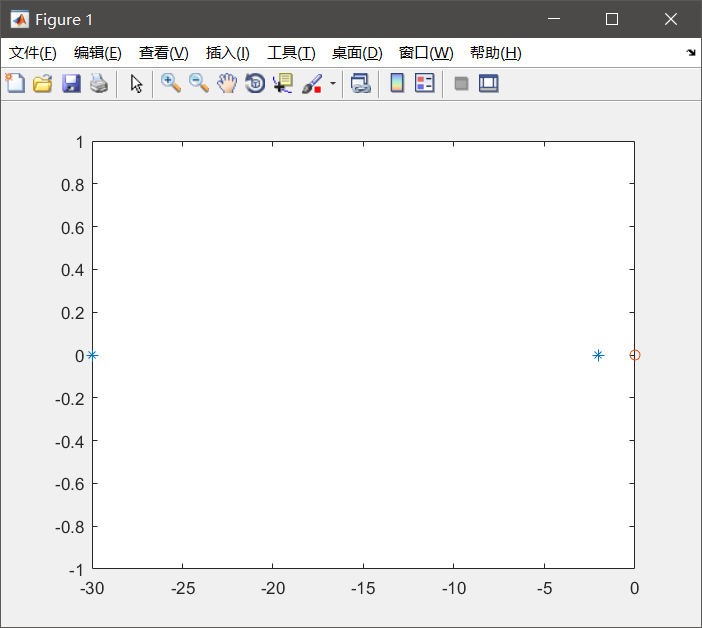
方法一

code

num = [1, 0];
den = [1,32,60];
[r,poles,k]=residue(num,den);
p=roots(den);
z=roots(num);
plot(real(p),imag(p),'*');hold on;
plot(real(z),imag(z),'o');hold on;

结果

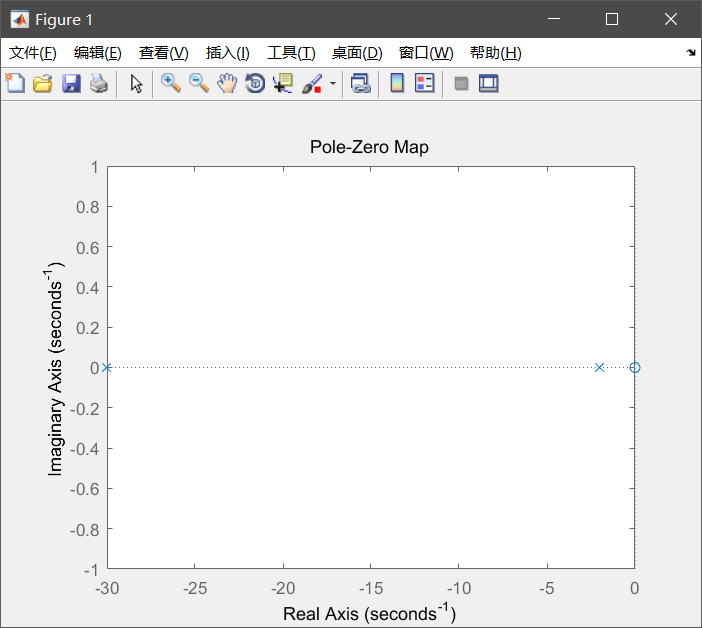
方法二

code

num = [1, 0];
den = [1,32,60];
sys = tf(num,den);
pzmap(sys);

结果

题（2）绘出系统的脉冲响应曲线，并观察t→∞时，脉冲响应变化趋势

参考方法

2.用Matlab分析连续系统的时间响应

(1)脉冲响应 y=impulse(num,den,T)

y=impulse(num,den,T)
T:为等间隔的时间向量，指明要计算响应的时间点。

(2)阶跃响应 y=setp(num,den,T)

y=setp(num,den,T)
T:同上。

(3)对任意输入的响应 y=lsim(num,den,U,T)

y=lsim(num,den,U,T)
U:任意输入信号，T:同上。

条件一

code

num = [1, 0];
den = [1,32,60];
T = 0:0.1:2;
y= impulse(num,den,T);
plot(T,y);

结果

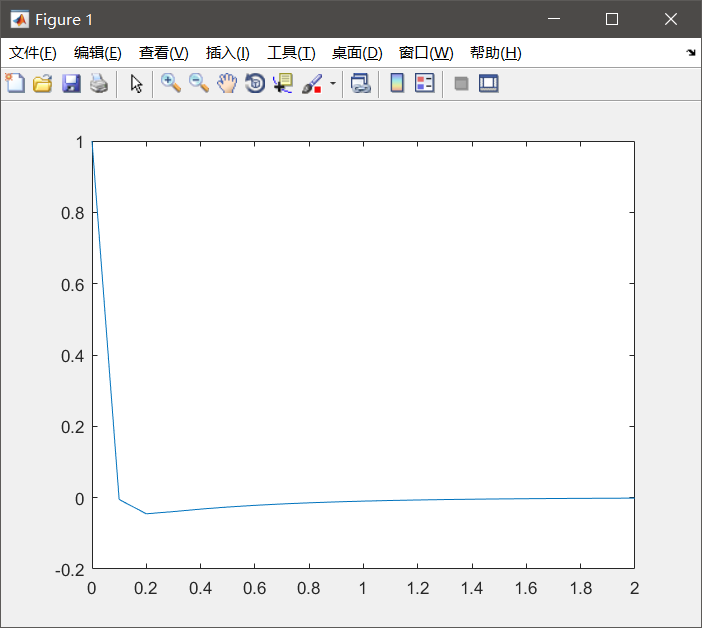
当t→∞时，脉冲响应趋于0；

条件二

code

num = [1, 0];
den = [1,-1,-6];
T = 0:0.1:2;
y= impulse(num,den,T);
plot(T,y);

结果

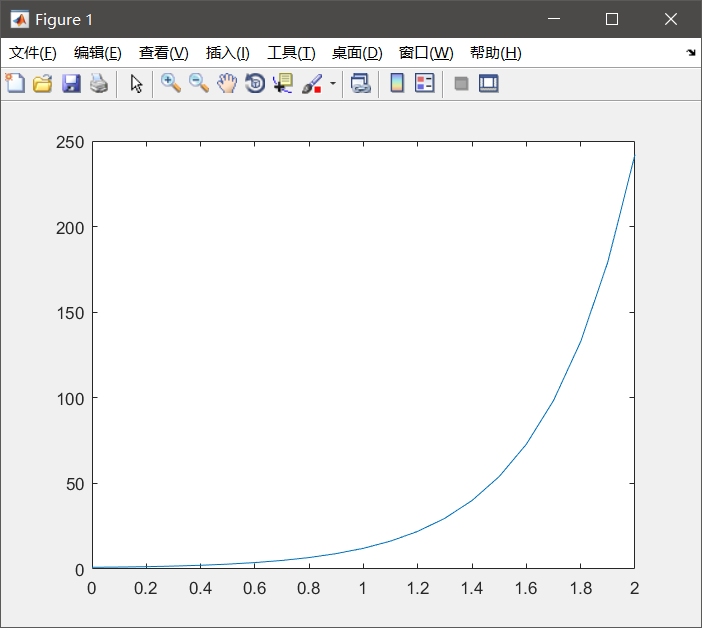
当t→∞时，脉冲响应趋于无穷大；

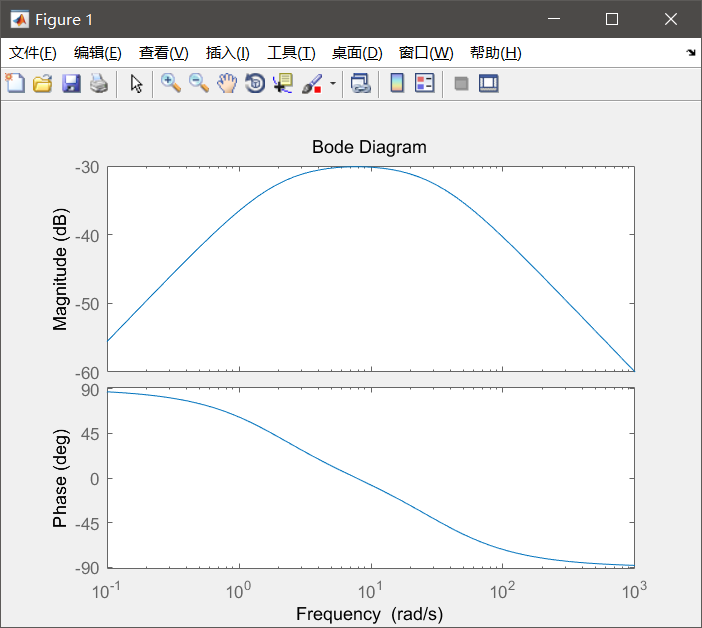
题(3)绘出系统的频响曲线

参考

MATLAB环境下频率响应曲线的绘制方法第21页

bode(sys)

bode(sys) creates a Bode plot of the frequency response of a dynamic system model sys. The plot displays the magnitude (in dB) and phase (in degrees) of the system response as a function of frequency.

code

num = [1, 0];
den = [1,32,60];
bode(num,den);

结果

第二大题

参考

filter()

Matlab中，filter函数可用来在给定输入和差分方程系数时求差分方程的数值解，
调用格式为：Y=filter(B,A,X)
其中：B=[b0,b1,…,bm];A=[a0,a1,…,an];X为输入信号序列，注意必须保证系数a0不为零。

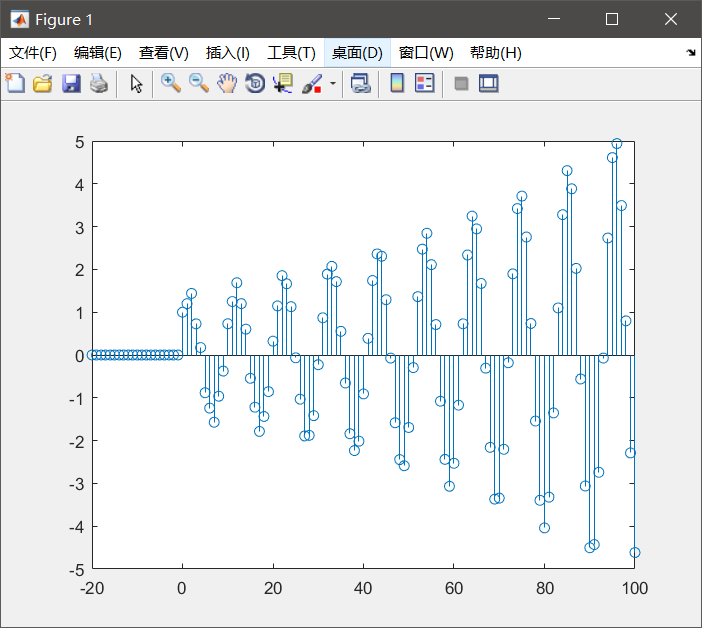
内容

利用filter命令求下面系统的冲激响应：
y(n)-0.7y(n-1)-0.6y(n-2)+y(n-3)=x(n)+0.5x(n-1)

code

A=[1,-0.7,-0.6,1];
B=[1,0.5];
n=[-20:100];
X=[n==0];
y=filter(B,A,X);
stem(n,y);

结果

最后

以上就是精明衬衫为你收集整理的《信号与系统》 实验四 系统响应的仿真参考第一大题第二大题的全部内容，希望文章能够帮你解决《信号与系统》 实验四 系统响应的仿真参考第一大题第二大题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。