目录
- 1.题目一
- 2.题目二
- 3.题目三
- 4.题目四
- 5.题目五
1.题目一
采用脉冲响应不变法设计一个巴特沃兹数字带通滤波器,要求:通带
;阻带
,滤波器采样频率
。试显示数字滤波器的幅频特性和零极点分布图,并写出该系统的传递函数。
先用模拟原型滤波器设计模拟带通滤波器,再使用impinvar函数,通过脉冲响应不变法计算数字滤波器的系数,从而得出幅频特性和零极点分布图如下:
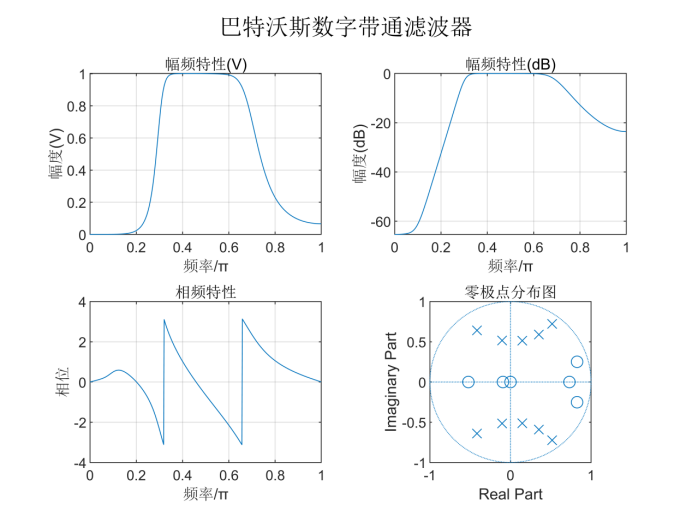
由频率特性曲线可知,该巴特沃斯数字带通滤波器在通阻带截止频率处能满足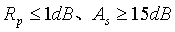 的设计指标要求,且系统的10个极点全部在单位圆内,是一个稳定的系统。系统的零点有部分在单位圆外,但并不影响系统的稳定性。
的设计指标要求,且系统的10个极点全部在单位圆内,是一个稳定的系统。系统的零点有部分在单位圆外,但并不影响系统的稳定性。
系统传递函数的分子系数和分母系数如下:

可写出该系统的传递函数为:
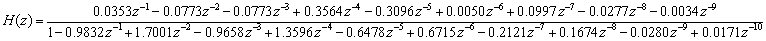
clear;
wp1=0.3*pi;wp2=0.7*pi;%数字滤波器的通带截止频率
ws1=0.1*pi;ws2=0.9*pi;%数字滤波器的阻带截止频率
Rp=1;As=15; %输入滤波器的通阻带衰减指标
%转换为模拟滤波器指标
Fs=2000;T=1/Fs;
Omgp1=wp1*Fs;Omgp2=wp2*Fs;%模拟滤波器的通带截止频率
Omgp=[Omgp1,Omgp2];
Omgs1=ws1*Fs;Omgs2=ws2*Fs;%模拟滤波器的阻带截止频率
Omgs=[Omgs1,Omgs2];
bw=Omgp2-Omgp1;w0=sqrt(Omgp1*Omgp2);%模拟通带带宽和中心频率
%模拟原型滤波器计算
[n,Omgn]=buttord(Omgp,Omgs,Rp,As,'s');%计算阶数n和截止频率
[z0,p0,k0]=buttap(n);%设计归一化的模拟原型滤波器
ba1=k0*real(poly(z0));%求原型滤波器系数b
aa1=real(poly(p0));%求原型滤波器系数a
[ba,aa]=lp2bp(ba1,aa1,w0,bw);%变换为模拟带通滤波器
%用脉冲响应不变法计算数字滤波器系数
[bd,ad]=impinvar(ba,aa,Fs)
%求数字系统的频率特性
[H,w]=freqz(bd,ad);
dbH=20*log10((abs(H)+eps)/max(abs(H)));%化为分贝值
%绘图
figure;
subplot(2,2,1);plot(w/pi,abs(H));
grid on;box on;title('幅频特性(V)');
xlabel('频率/π');ylabel('幅度(V)');
subplot(2,2,2);plot(w/pi,dbH);
grid on;box on;title('幅频特性(dB)');
xlabel('频率/π');ylabel('幅度(dB)');
subplot(2,2,3);plot(w/pi,angle(H));
grid on;box on;title('相频特性');
xlabel('频率/π');ylabel('相位');
subplot(2,2,4);zplane(bd,ad); %绘制零极点图
title('零极点分布图')
axis([-1,1,-1,1])
suptitle('巴特沃斯数字带通滤波器')
2.题目二
采用脉冲响应不变法设计一个切比雪夫II型带阻滤波器,要求:通带在
范围,
;阻带在
范围,
,滤波器采样频率
。在同一图形界面上显示原模拟带阻滤波器和数字带阻滤波器的幅频特性,观察频响特性的混叠现象。
先用模拟原型滤波器设计模拟带阻滤波器,再使用impinvar函数,通过脉冲响应不变法计算数字滤波器的系数,从而得出模拟带阻滤波器和数字带阻滤波器的幅频特性如下:
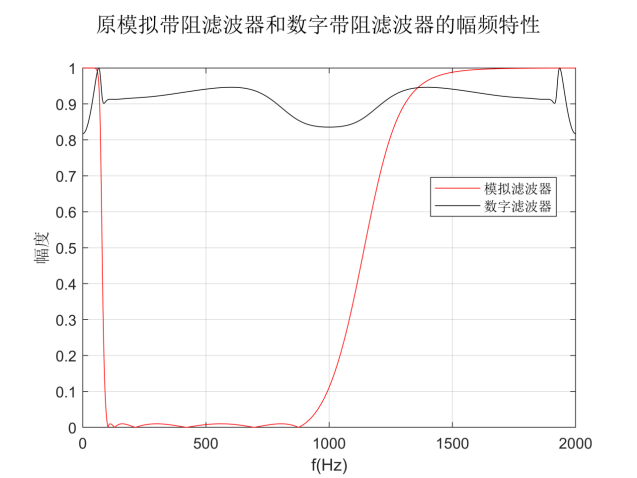
图中红线表现了原模拟带阻滤波器的幅频曲线,黑线表现了数字带阻滤波器的幅频曲线。图形横轴取0-Fs的频率范围,可以看出,使用脉冲响应不变法设计带阻滤波器,频率特性将产生严重的混叠现象,因此脉冲响应不变法不适用于高通和带阻滤波器,因为它们在高频区幅频特性不等于零。
clear;
wp1=0.1*pi;wp2=0.9*pi;%数字滤波器的通带截止频率
ws1=0.3*pi;ws2=0.7*pi;%数字滤波器的阻带截止频率
Rp=1;As=40; %输入滤波器的通阻带衰减指标
%转换为模拟滤波器指标
Fs=2000;T=1/Fs;
Omgp1=wp1*Fs;Omgp2=wp2*Fs;%模拟滤波器的通带截止频率
Omgp=[Omgp1,Omgp2];
Omgs1=ws1*Fs;Omgs2=ws2*Fs;%模拟滤波器的阻带截止频率
Omgs=[Omgs1,Omgs2];
bw=Omgp2-Omgp1;w0=sqrt(Omgp1*Omgp2);%模拟通带带宽和中心频率
%模拟原型滤波器计算
[n,Omgn]=cheb2ord(Omgp,Omgs,Rp,As,'s');%计算阶数n和截止频率
[z0,p0,k0]=cheb2ap(n,As);%设计归一化的模拟原型滤波器
ba1=k0*real(poly(z0));%求原型滤波器系数b
aa1=real(poly(p0));%求原型滤波器系数a
[ba,aa]=lp2bs(ba1,aa1,w0,bw);%变换为模拟带阻滤波器
%用脉冲响应不变法计算数字滤波器系数
[bd,ad]=impinvar(ba,aa,Fs);
%模拟滤波器与数字滤波器的幅频响应
wb=[0:Fs]*2*pi;%为作图建立频率向量
Ha=freqs(ba,aa,wb);%计算模拟频率响应
H=freqz(bd,ad,wb/Fs);%计算数字频率响应
plot(wb/(2*pi),abs(Ha)/max(abs(Ha)),'r'),hold on
plot(wb/(2*pi),abs(H)/max(abs(H)),'k');
xlabel('f(Hz)');ylabel('幅度');
suptitle('原模拟带阻滤波器和数字带阻滤波器的幅频特性')
grid on
legend('模拟滤波器','数字滤波器','Location','best');
3.题目三
用双线性变换法设计切比雪夫II型数字带通滤波器,要求:通带
;阻带
,滤波器采样频
率,列出传递函数并作出频率响应曲线和零极点分布图。
先用模拟原型滤波器设计模拟带通滤波器,再使用bilinear函数,通过双线性变换法计算数字滤波器的系数,从而得出幅频特性和零极点分布图如下:
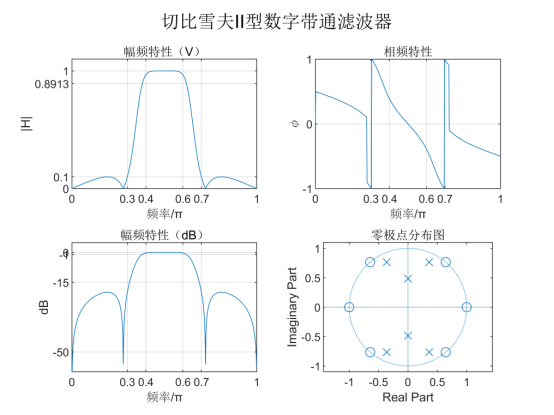
由频率特性曲线可知,该切比雪夫II型数字带通滤波器在通阻带截止频率处能满足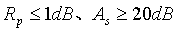 的设计指标要求。由n=3可知,由3阶的模拟低通原型用双线性变换法设计出来的切比雪夫II型数字带通滤波器是一个6阶的系统,且系统的6个极点全部在单位圆内,是一个稳定的系统。
的设计指标要求。由n=3可知,由3阶的模拟低通原型用双线性变换法设计出来的切比雪夫II型数字带通滤波器是一个6阶的系统,且系统的6个极点全部在单位圆内,是一个稳定的系统。
系统传递函数的分子系数和分母系数如下:

可写出该系统的传递函数为:
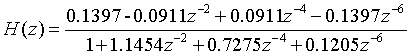
clear;
%数字滤波器指标
Fs=1000;T=1/Fs;
fp1=200;wp1=fp1/Fs*2*pi;%数字滤波器的通带截止频率
fp2=300;wp2=fp2/Fs*2*pi;
fs1=150;ws1=fs1/Fs*2*pi;%数字滤波器的阻带截止频率
fs2=350;ws2=fs2/Fs*2*pi;
Rp=1;As=20; %输入滤波器的通阻带衰减指标
ripple=10^(-Rp/20);
Attn=10^(-As/20);
%转换为模拟滤波器指标
Omgp1=(2/T)*tan(wp1/2);Omgp2=(2/T)*tan(wp2/2);
Omgp=[Omgp1 Omgp2];
Omgs1=(2/T)*tan(ws1/2);Omgs2=(2/T)*tan(ws2/2);
Omgs=[Omgs1 Omgs2];
bw=Omgs2-Omgs1;w0=sqrt(Omgs1*Omgs2);%模拟通带带宽和中心频率
%模拟原型滤波器计算
[n,Omgn]=cheb2ord(Omgp,Omgs,Rp,As,'s');%计算阶数n和截止频率
[z0,p0,k0]=cheb2ap(n,As);%设计归一化的模拟原型滤波器
ba1=k0*real(poly(z0));%求原型滤波器系数b
aa1=real(poly(p0));%求原型滤波器系数a
[ba,aa]=lp2bp(ba1,aa1,w0,bw);%变换为模拟带通滤波器
%用双线性变换法计算数字滤波器系数
[bd,ad]=bilinear(ba,aa,Fs)%计算数字滤波器系数
%求数字系统的频率特性
[H,w]=freqz(bd,ad);
dbH=20*log10((abs(H)+eps)/max(abs(H)));%化为分贝值
%绘图
subplot(2,2,1),plot(w/pi,abs(H));title('幅频特性(V)');
xlabel('频率/π');ylabel('|H|');axis([0,1,0,1.1]);
set(gca,'XTickMode','manual','XTick',[0,ws1/pi,wp1/pi,wp2/pi,ws2/pi,1])
set(gca,'YTickMode','manual','YTick',[0,Attn,ripple,1]);grid on
subplot(2,2,2),plot(w/pi,angle(H)/pi);title('相频特性');
xlabel('频率/π');ylabel('phi');axis([0,1,-1,1]);
set(gca,'XTickMode','manual','XTick',[0,ws1/pi,wp1/pi,wp2/pi,ws2/pi,1])
set(gca,'YTickMode','manual','YTick',[-1,0,1]);grid on
subplot(2,2,3),plot(w/pi,dbH);title('幅频特性(dB)');
xlabel('频率/π');ylabel('dB');axis([0,1,-60,5]);
set(gca,'XTickMode','manual','XTick',[0,ws1/pi,wp1/pi,wp2/pi,ws2/pi,1])
set(gca,'YTickMode','manual','YTick',[-50,-15,-1,0]);grid on
subplot(2,2,4);zplane(bd,ad); %绘制零极点图
title('零极点分布图')
suptitle('切比雪夫II型数字带通滤波器')
4.题目四
采用双线性变化法设计一个椭圆数字带阻滤波器,要求:下通带
,上通带
,阻带下限
,阻带上限
,滤波器采样周期T=0.1s。列出传递函数并作出频率响应曲线和零极点分布图。
先用模拟原型滤波器设计模拟带阻滤波器,再使用bilinear函数,通过双线性变换法计算数字滤波器的系数,从而得出幅频特性和零极点分布图如下:
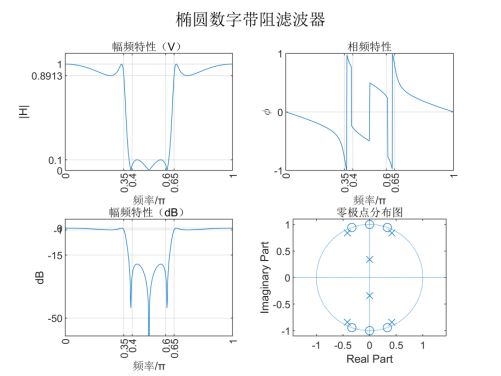
由频率特性曲线可知,该椭圆数字带阻滤波器在通阻带截止频率处能满足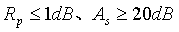 的设计指标要求。由n=3可知,由3阶的模拟低通原型用双线性变换法设计出来的椭圆数字带阻滤波器是一个6阶的系统,且系统的6个极点全部在单位圆内,是一个稳定的系统。
的设计指标要求。由n=3可知,由3阶的模拟低通原型用双线性变换法设计出来的椭圆数字带阻滤波器是一个6阶的系统,且系统的6个极点全部在单位圆内,是一个稳定的系统。
系统传递函数的分子系数和分母系数如下:

可写出该系统的传递函数为:
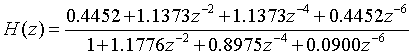
clear;
wp1=0.35*pi;wp2=0.65*pi;%数字滤波器的通带截止频率
ws1=0.4*pi;ws2=0.6*pi;%数字滤波器的阻带截止频率
Rp=1;As=20; %输入滤波器的通阻带衰减指标
ripple=10^(-Rp/20);
Attn=10^(-As/20);
T=0.1;Fs=1/T;
%转换为模拟滤波器指标
Omgp1=(2/T)*tan(wp1/2);Omgp2=(2/T)*tan(wp2/2);
Omgp=[Omgp1 Omgp2];
Omgs1=(2/T)*tan(ws1/2);Omgs2=(2/T)*tan(ws2/2);
Omgs=[Omgs1 Omgs2];
bw=Omgp2-Omgp1;w0=sqrt(Omgp1*Omgp2);%模拟通带带宽和中心频率
%模拟原型滤波器计算
[n,Omgn]=ellipord(Omgp,Omgs,Rp,As,'s');%计算阶数n和截止频率
[z0,p0,k0]=ellipap(n,Rp,As);%设计归一化的模拟原型滤波器
ba1=k0*real(poly(z0));%求原型滤波器系数b
aa1=real(poly(p0));%求原型滤波器系数a
[ba,aa]=lp2bs(ba1,aa1,w0,bw);%变换为模拟带通滤波器
%用双线性变换法计算数字滤波器系数
[bd,ad]=bilinear(ba,aa,Fs)%计算数字滤波器系数
%求数字系统的频率特性
[H,w]=freqz(bd,ad);
dbH=20*log10((abs(H)+eps)/max(abs(H)));%化为分贝值
%绘图
subplot(2,2,1),plot(w/pi,abs(H));title('幅频特性(V)');
xlabel('频率/π');ylabel('|H|');axis([0,1,0,1.1]);
set(gca,'XTickMode','manual','XTick',[0,wp1/pi,ws1/pi,ws2/pi,wp2/pi,1])
set(gca,'XtickLabelRotation',90);
set(gca,'YTickMode','manual','YTick',[0,Attn,ripple,1]);grid on
subplot(2,2,2),plot(w/pi,angle(H)/pi);title('相频特性');
xlabel('频率/π');ylabel('phi');axis([0,1,-1,1]);
set(gca,'XTickMode','manual','XTick',[0,wp1/pi,ws1/pi,ws2/pi,wp2/pi,1])
set(gca,'XtickLabelRotation',90);
set(gca,'YTickMode','manual','YTick',[-1,0,1]);grid on
subplot(2,2,3),plot(w/pi,dbH);title('幅频特性(dB)');
xlabel('频率/π');ylabel('dB');axis([0,1,-60,5]);
set(gca,'XTickMode','manual','XTick',[0,wp1/pi,ws1/pi,ws2/pi,wp2/pi,1])
set(gca,'XtickLabelRotation',90);
set(gca,'YTickMode','manual','YTick',[-50,-15,-1,0]);grid on
subplot(2,2,4);zplane(bd,ad); %绘制零极点图
title('零极点分布图')
suptitle('椭圆数字带阻滤波器')
5.题目五
用MATLAB直接法设计切比雪夫II型数字低通滤波器,要求:通带
;阻带
。请描绘滤波器归一化的绝对和相对幅频特性、相频特性、零极点分布图,列出系统传递函数式。
直接使用cheb2ord函数求出切比雪夫II型数字低通滤波器的阶数N和截止频率wc,再使用cheby2函数直接求出数字低通滤波器的系数,进而画出归一化的绝对和相对幅频特性、相频特性、零极点分布图:
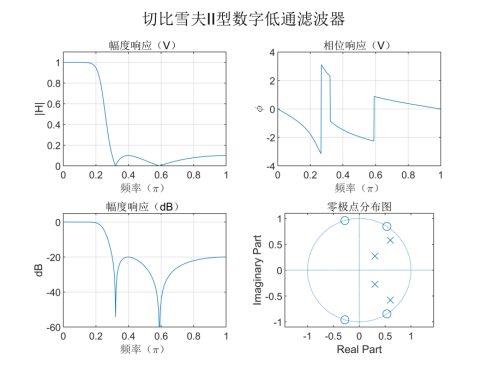
由上图所示,这是一个归一化的频率响应曲线,基本满足通阻带的设计要求,改系统是一个4阶的切比雪夫II型数字带通滤波器。
系统传递函数的分子系数和分母系数如下:

可写出该系统的传递函数为:
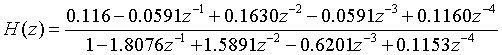
clear;
wp=0.2;%数字滤波器的阻带截止频率
ws=0.3;
Rp=1;As=20;%输入滤波器的通阻带衰减指标
[n,wc]=cheb2ord(wp,ws,Rp,As);%计算阶数n和截止频率
[b,a]=cheby2(n,As,wc)%直接求数字低通滤波器系数
[H,w]=freqz(b,a);%求数字系统的频率特性
dbH=20*log10((abs(H)+eps)/max(abs(H)));%化为分贝值
subplot(2,2,1);plot(w/pi,abs(H));title('幅度响应(V)');
ylabel('|H|');xlabel('频率(pi)');axis([0,1,0,1.1]);grid
subplot(2,2,2);plot(w/pi,angle(H));title('相位响应(V)');
ylabel('phi');xlabel('频率(pi)');grid
subplot(2,2,3);plot(w/pi,dbH);title('幅度响应(dB)');
ylabel('dB');xlabel('频率(pi)');axis([0,1,-60,5]);grid
subplot(2,2,4);zplane(b,a);title('零极点分布图')
suptitle('切比雪夫II型数字低通滤波器')
最后
以上就是糊涂火龙果最近收集整理的关于数字信号处理实验81.题目一2.题目二3.题目三4.题目四5.题目五的全部内容,更多相关数字信号处理实验81内容请搜索靠谱客的其他文章。
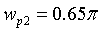








发表评论 取消回复