概述
一.矩阵的计算
1.特殊矩阵的生成
2.矩阵的数学运算
1.四则运算加减乘除，+，-，*，/,,除法之中，右除是先求矩阵的逆，然后再乘。而左除法，不需要进行逆运算，可以避免奇异性带来的麻烦。右除要快一点。
2.与常数相关的操作 进行除法时候，常数只能作为除数
3.基本函数运算
- det(a) %求a的行列式
- eig(a) %求矩阵的特征值
- inv(a)或者a^(-1) %求矩阵a的逆矩阵
- rank(a) %求矩阵的矩
- trace(a) %求矩阵的秩（对角线元素之和）
3.矩阵的数组运算
矩阵对应元素的计算。“点”，运算。
（1）数组的加减法和矩阵的加减法完全一样，数组的乘除法是指两同维数组对应元素的乘除法，运算符为“.*”，“./”,"."。另外矩阵的数组运算还有幂运算（.^）、指数运算（exp）,对数运算（log）,开方运算（sqrt）等。有了对应元素的规定，数组的运算实质就是针对数组内部的每个元素进行的。
（2）逻辑关系运算
| 符号运算符 | 功能 | 函数名 |
| <= | 小于等于 | le |
| >= | 大于等于 | ge |
| & | 逻辑与 | and |
| | | 逻辑或 | or |
| ~ | 逻辑非 | not |
二.常用函数
collect()%合并同类项
expend()%展开符号表达式
factor() %符号表达式因式分解
simple() %符号表达式的化简
limit(F,x,a)%当x->a时，表达式F的极限
limit(F,a)%默认自变量时，趋向a的极限
limit(F)%默认自变量，默认a为0
limit(F,x,a,'left')%取F的右极限
limit(F,x,a,'right')%取F的右极限
%若极限不存在，则返回NaN
diff(f)%对默认变量求f的微分
diff(f,v)%最指定变量v求微分
diff(f,n)%对默认变量求n阶微分
diff(f,v,n)%对制定变量v求f的n阶微分
int(f)%对f表达式的默认变量求不定积分
int(f,v)%对指定变量求不定积分
int(f,v,a,b)%对指定变量v在（a,b）区间上求积分
taylor(f,n,v)%n阶泰勒级数展开
F=fourier(f)
F=fourier(f,v)
F=fourier(f,u,v)%Fourier积分变换
F=ifourier(f)
F=ifourier(f,v)
F=ifourier(f,u,v)%ifourier函数
L=Laplace(F)%Laplace变换
L=Laplace(F,t)
L=Laplace(F,w,z)
L=ilaplace(F)%逆Laplace变换
L=ilaplace(F,t)
L=ilaplace(F,w,z)
solve(f)%求线性方程f=0时的解
solve(f,'t')%对指定变量t求解
solve(f1,f2,...,fn)%求n个方程的解
dsolve('eq1','eq2',...,'cond1','cond2',...,'v')%eq1,eq2,...为微分方程，至多对12个微分方程进行求解；'cond1','cond2'...为初始条件；'v'为指定自变量，默认是't'；
%微分方程各阶导数均以大写字母D表示，如y的一阶导数可以表示为Dy,y的二阶导数d2y/dx2可以表示为D2y,同理，y的n阶导可以表示为Dny
%ezplot(y),进行符号函数绘图
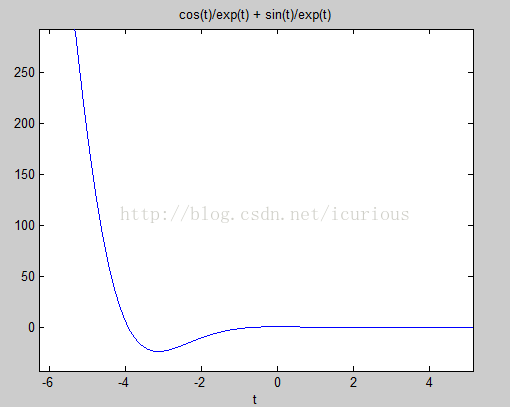
最后
以上就是甜甜黑米为你收集整理的【Matllab】笔记（1）——矩阵操作符和常用函数的全部内容，希望文章能够帮你解决【Matllab】笔记（1）——矩阵操作符和常用函数所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复