文章目录
- 0. 受控对象与设计要求
- 0.1 受控对象
- 0.2 设计要求
- 1. 控制系统结构
- 2. PID控制器设计
- 3. 那小车呢?
- 4. 几个问题
- 5. 参考
0. 受控对象与设计要求
这里列出上一篇文章的结果
0.1 受控对象
P
p
e
n
d
(
s
)
=
Φ
(
s
)
U
(
s
)
=
m
l
q
s
s
3
+
b
(
I
+
m
l
2
)
q
s
2
−
(
M
+
m
)
m
g
l
q
s
−
b
m
g
l
q
[
r
a
d
N
]
P_{pend}(s) = frac{Phi(s)}{U(s)}=frac{frac{ml}{q}s}{s^3+frac{b(I+ml^2)}{q}s^2-frac{(M+m)mgl}{q}s-frac{bmgl}{q}} qquad [ frac{rad}{N}]
Ppend(s)=U(s)Φ(s)=s3+qb(I+ml2)s2−q(M+m)mgls−qbmglqmls[Nrad]
P
c
a
r
t
(
s
)
=
X
(
s
)
U
(
s
)
=
(
I
+
m
l
2
)
s
2
−
g
m
l
q
s
4
+
b
(
I
+
m
l
2
)
q
s
3
−
(
M
+
m
)
m
g
l
q
s
2
−
b
m
g
l
q
s
[
m
N
]
P_{cart}(s) = frac{X(s)}{U(s)} = frac{ frac{ (I+ml^2)s^2 - gml } {q} }{s^4+frac{b(I+ml^2)}{q}s^3-frac{(M+m)mgl}{q}s^2-frac{bmgl}{q}s} qquad [ frac{m}{N}]
Pcart(s)=U(s)X(s)=s4+qb(I+ml2)s3−q(M+m)mgls2−qbmglsq(I+ml2)s2−gml[Nm]
其中:
q
=
[
(
M
+
m
)
(
I
+
m
l
2
)
−
(
m
l
)
2
]
q=[(M+m)(I+ml^2)-(ml)^2]
q=[(M+m)(I+ml2)−(ml)2]
0.2 设计要求
对于倒立摆,当小车受到1Nsec的冲激响应的时候:
- θ的稳定时间 < 5s
- |θ-θ0| < 0.05 radians
对于整个系统,当小车收到0.2m的阶跃信号的时候:
- x 与 θ 的稳定时间 < 5s
- x 的上升时间 < 0.5s
- |θ-θ0| < 0.05 radians (也就是20°)
- 对于x和θ来说,稳态误差 < 2%
1. 控制系统结构
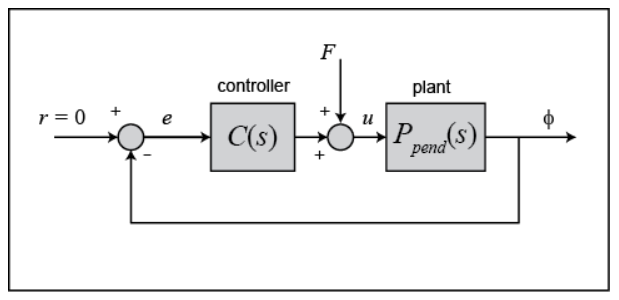
上图是我们常用的控制器结构。但是因为这里我们希望倒立摆尽可能地抵抗干扰F,从而保持平衡在垂直位置,系统的输入为零。这种0输入,抵抗干扰的控制问题我们一般统称为 Regulator problem。通过简单的变形,我们得到新的控制系统框图:
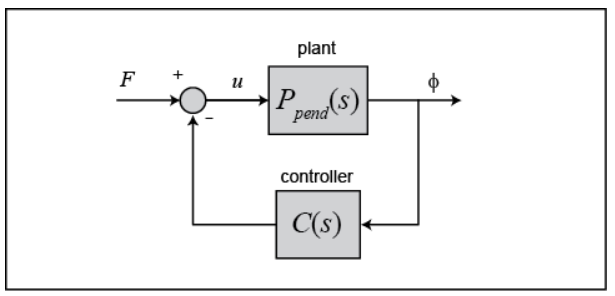
该系统的转换方程为:
T
(
s
)
=
Φ
(
s
)
F
(
s
)
=
P
p
e
n
d
(
s
)
1
+
C
(
s
)
P
p
e
n
d
(
s
)
T(s) = frac{Phi(s)}{F(s)} = frac{P_{pend}(s)}{1 + C(s)P_{pend}(s)}
T(s)=F(s)Φ(s)=1+C(s)Ppend(s)Ppend(s)
在开始设计PID控制器之前,我们先在Matlab里面定义好我们的受控对象
M = 0.5;
m = 0.2;
b = 0.1;
I = 0.006;
g = 9.8;
l = 0.3;
q = (M+m)*(I+m*l^2)-(m*l)^2;
s = tf('s');
P_pend = (m*l*s/q)/(s^3 + (b*(I + m*l^2))*s^2/q - ((M + m)*m*g*l)*s/q - b*m*g*l/q);
2. PID控制器设计
通过观察控制系统框图,我们发现控制器在反馈线上,因此我们可以用Matlab自带的feedback函数来组成带有PID控制的新系统(这里我们先随机定三个PID参数):
Kp = 1;
Ki = 1;
Kd = 1;
C = pid(Kp,Ki,Kd);
T = feedback(P_pend,C);
干扰F在新系统里面变成了输入,现在我们看一下新系统受到冲激干扰时的响应:
t=0:0.01:10;
impulse(T,t)
title({'Response of Pendulum Position to an Impulse Disturbance';'under PID Control: Kp = 1, Ki = 1, Kd = 1'});
输出结果
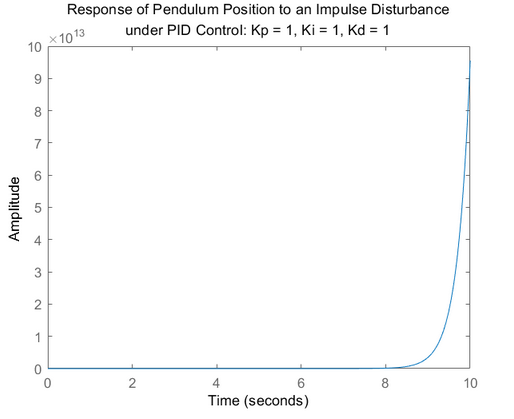
系统依旧不收敛,我们尝试增大P参数
Kp = 100;
Ki = 1;
Kd = 1;
C = pid(Kp,Ki,Kd);
T = feedback(P_pend,C);
t=0:0.01:10;
impulse(T,t)
axis([0, 2.5, -0.2, 0.2]);
title({'Response of Pendulum Position to an Impulse Disturbance';'under PID Control: Kp = 100, Ki = 1, Kd = 1'});
输出结果
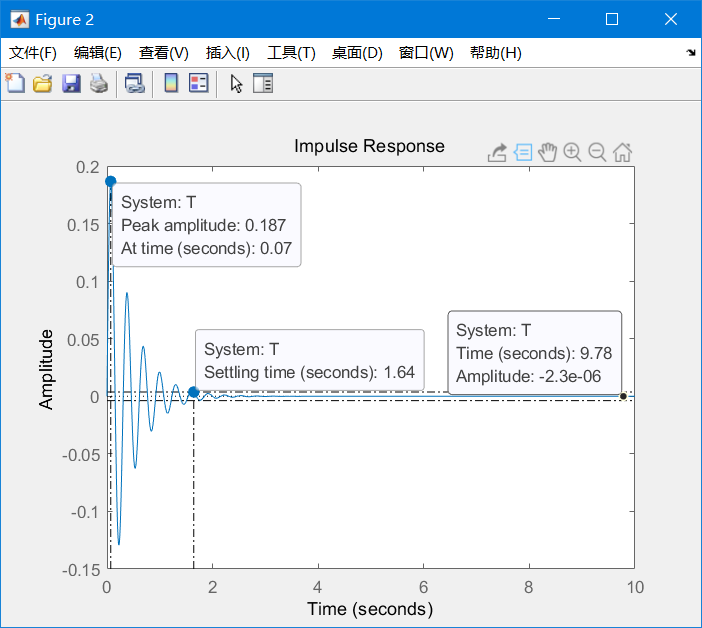
系统稳定了,有点震荡。对比我们的设计要求,稳态误差和稳定时间都满足了要求。但是超调很高,超出了0.05弧度的限制。对付超调我们可以通过适当增大D参数来实现。经过几轮尝试,我们最终确定Kp=100,Ki=1,Kd=20,新的输出:
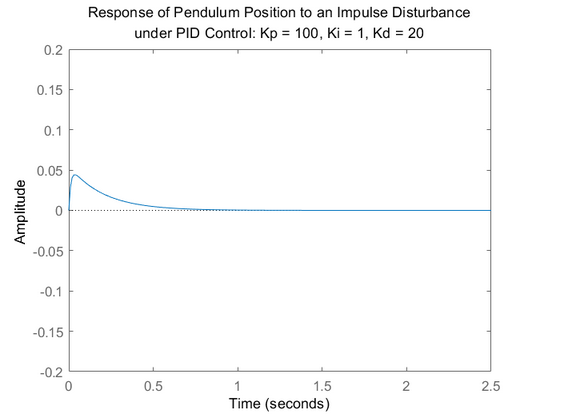
此时,我们设计的PID控制器已经满足所有设计要求。
3. 那小车呢?
上述讨论中系统框图其实是不完整的,因为该系统是单输入双输出系统。而我们并没有考虑小车的位置,一个完整的系统框图其实如下:
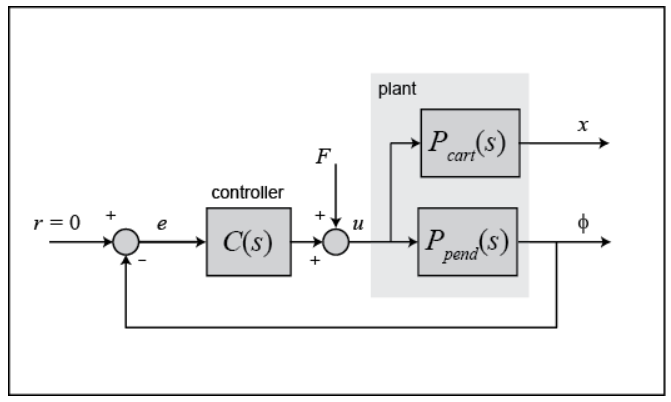
重新整理一下框图得到;
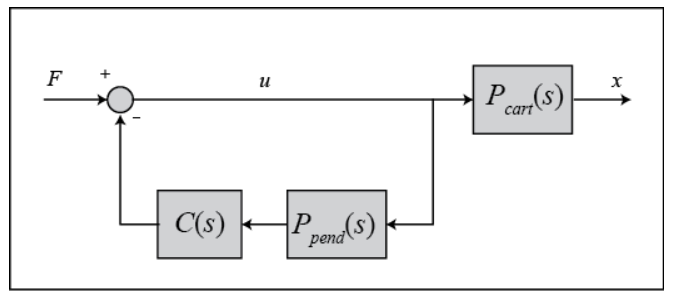
因此我们可以得到加了PID控制器后的新系统中小车位置相对于扰动F的转换方程:
T
2
(
s
)
=
X
(
s
)
F
(
s
)
=
P
c
a
r
t
(
s
)
1
+
P
p
e
n
d
(
s
)
C
(
s
)
T_2(s) = frac{X(s)}{F(s)} = frac{P_{cart}(s)}{1 + P_{pend}(s)C(s)}
T2(s)=F(s)X(s)=1+Ppend(s)C(s)Pcart(s)
其中
P
c
a
r
t
(
s
)
Pcart(s)
Pcart(s)与
C
(
s
)
C(s)
C(s)已知,于是可以获得该系统转换方程以及冲激响应:
P_cart = (((I+m*l^2)/q)*s^2 - (m*g*l/q))/(s^4 + (b*(I + m*l^2))*s^3/q - ((M + m)*m*g*l)*s^2/q - b*m*g*l*s/q);
T2 = feedback(1,P_pend*C)*P_cart;
t = 0:0.01:5;
impulse(T2, t);
title({'Response of Cart Position to an Impulse Disturbance';'under PID Control: Kp = 100, Ki = 1, Kd = 20'});
输出:
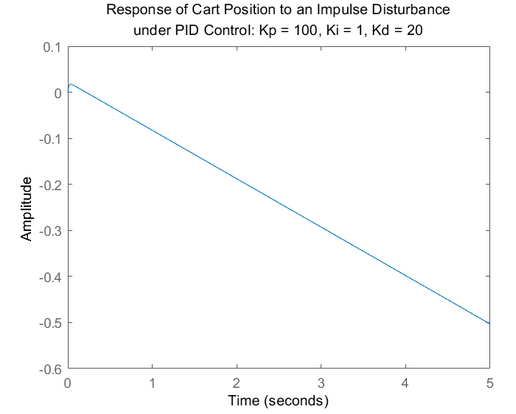
小车几乎以恒定速度往负方向运动,可见虽然我们控制好了倒立摆的角度,但是小车的位置不收敛,所以尽管理论上可以控制好倒立摆,但实际情况下我们不可能有一个无限长的通道供小车一直运动。
4. 几个问题
- 这里我们的干扰是施加在小车上的,那万一干扰施加在倒立摆上面呢?要怎么确定新的模型框图?
- 动力学方程里面我们控制的是小车受到的力F,但实际上我们方便控制的是小车的位置X,或者往一个方向的速度加速度,这种情况咋办?
5. 参考
https://ctms.engin.umich.edu/CTMS/index.php?example=InvertedPendulum§ion=ControlPID
最后
以上就是羞涩火龙果最近收集整理的关于Matlab 仿真——单自由度倒立摆(3)PID控制器设计的全部内容,更多相关Matlab内容请搜索靠谱客的其他文章。








发表评论 取消回复