wpdec2
Wavelet packet decomposition 2-D
Syntax
T = wpdec2(X,N,wname,E,P)
T = wpdec2(X,N,wname)
T = wpdec2(X,N,wname,'shannon')
Description
wpdec2 is a two-dimensional
wavelet packet analysis function.
T = wpdec2(X,N,wname,E,P) returns a wavelet packet
tree T corresponding to the wavelet packet decomposition of the
matrix X, at level N, with the specified wavelet
wname (see wfilters for more information).
T = wpdec2(X,N,wname) is equivalent to
T = wpdec2(X,N,wname,'shannon').
E is a character vector or string scalar containing the type of entropy and
P is an optional parameter depending on the value of
T (see wentropy for more information).
Entropy Type Name (E)Parameter (P)Comments'shannon'P is not used.
'log energy'P is not used.
'threshold'0 ≤ PP is the threshold.
'sure'0 ≤ PP is the threshold.
'norm'1 ≤ PP is the power.
'user'Character vector or string scalarP is a character vector or string scalar
containing the file name of your own entropy function, with a single
input X.
FunNameNo constraints on PFunName is any other character vector or
string scalar except those used for the previous Entropy Type
Names listed above.
FunName
contains the file name of your own entropy function, with
X as input and P as
additional parameter to your entropy function.
Note
The 'user' option is historical and still
kept for compatibility, but it is obsoleted by the last option described
in the preceding table. The FunName option does
the same as the 'user' option and in addition,
allows you to pass a parameter to your own entropy function.
See wpdec for a more
complete description of the wavelet packet decomposition.
Examples
% The current extension mode is zero-padding (see dwtmode).
% Load image.
load tire
% X contains the loaded image.
% For an image the decomposition is performed using:
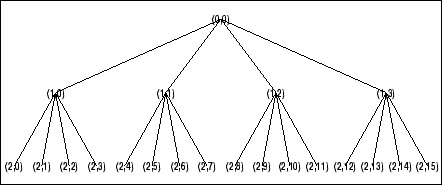
t = wpdec2(X,2,'db1');
% The default entropy is shannon.
% Plot wavelet packet tree
% (quarternary tree, or tree of order 4).
plot(t)
Tips
When X represents an indexed image, X is an m-by-n matrix.
When X represents a truecolor image, it is an m-by-n-by-3
array, where each m-by-n matrix
represents a red, green, or blue color plane concatenated along the
third dimension.
For more information on image formats, see the image and imfinfo reference
pages.
Algorithms
The algorithm used for the wavelet packets decomposition follows
the same line as the wavelet decomposition process (see dwt2 and wavedec2 for
more information).
References
Coifman, R.R.; M.V. Wickerhauser (1992), “Entropy-based
algorithms for best basis selection,” IEEE Trans.
on Inf. Theory, vol. 38, 2, pp. 713–718.
Meyer, Y. (1993), Les ondelettes. Algorithmes et applications,
Colin Ed., Paris, 2nd edition. (English translation: Wavelets:
Algorithms and Applications, SIAM).
Wickerhauser, M.V. (1991), “INRIA lectures on wavelet
packet algorithms,” Proceedings ondelettes et paquets
d'ondes, 17–21 June, Rocquencourt, France, pp. 31–99.
Wickerhauser, M.V. (1994), Adapted wavelet analysis
from theory to software Algorithms, A.K. Peters.
Introduced before R2006a
最后
以上就是笨笨唇膏最近收集整理的关于matlab中wpdec,Wavelet packet decomposition 2-D的全部内容,更多相关matlab中wpdec,Wavelet内容请搜索靠谱客的其他文章。







发表评论 取消回复