概述
博客已搬家，欢迎访问新居：http://lukeyalvin.site，主要涉及SLAM相关方向，目前知识积累尚浅，多多指教！
第二节 控制系统的数学模型——传递函数
了解数学模型的概念，自动控制原理都包含哪些数学模型，怎样将系统转换为数学模型
什么是控制系统的数学模型？控制系统的模型有哪些种？
数学模型是用来描述系统因果关系的数学表达式。有微分方程、传递函数、结构框图、信号流图、频率特性、差分方程、状态方程、传递矩阵等表达形式。
什么是控制系统的数学模型？控制系统的模型有哪些种？
数学模型是用来描述系统因果关系的数学表达式。有微分方程、传递函数、结构框图、信号流图、频率特性、差分方程、状态方程、传递矩阵等表达形式。
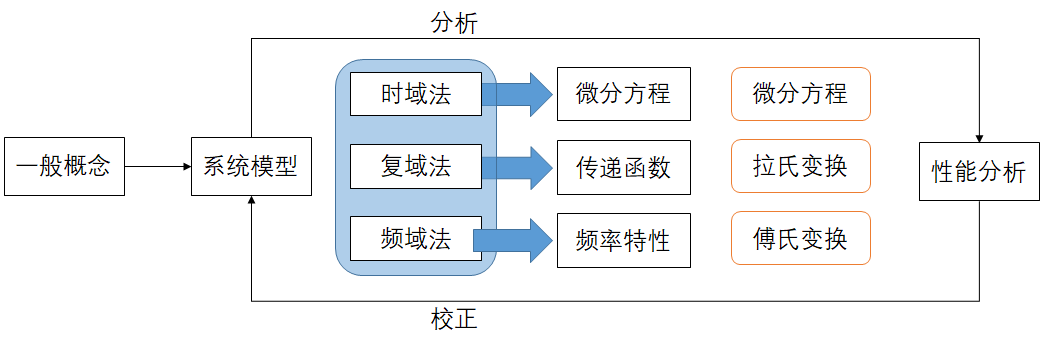
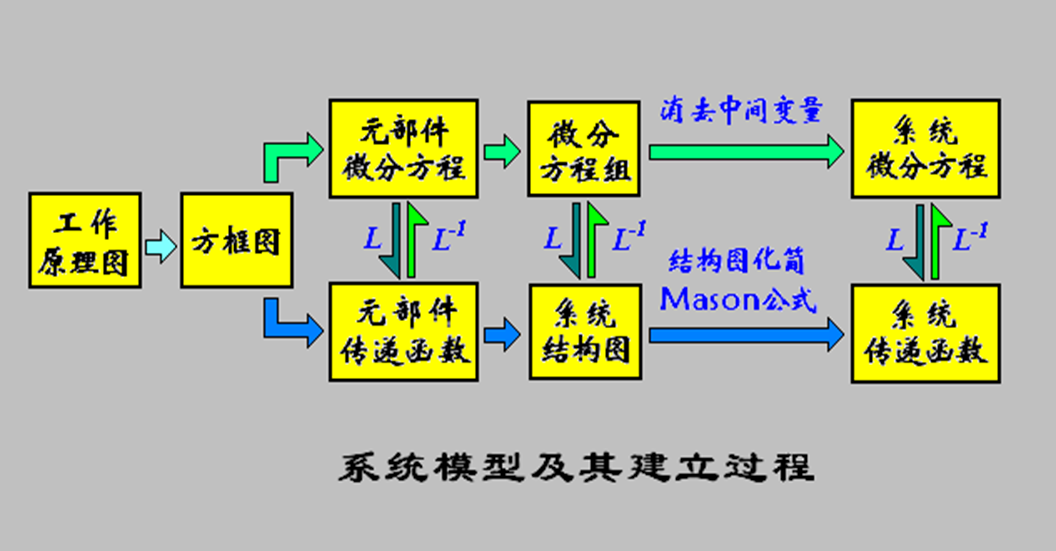
系统数学模型建立的过程：
微分方程
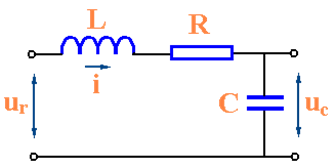
RLC电路微分方程的建立（二阶）
u
r
(
t
)
=
L
d
i
(
t
)
d
t
+
R
i
(
t
)
+
u
c
(
t
)
i
(
t
)
=
C
d
u
c
(
t
)
d
t
u
r
(
t
)
=
L
C
d
2
u
c
(
t
)
d
t
2
+
R
C
d
u
c
(
t
)
d
t
+
u
c
(
t
)
u_r(t)=Lfrac{d_i(t)}{dt}+R_i(t)+u_c(t)\ i(t)=Cfrac{du_c(t)}{dt}\ u_r(t)=LCfrac{d^2u_c(t)}{dt^2}+RCfrac{du_c(t)}{dt}+u_c(t)
ur(t)=Ldtdi(t)+Ri(t)+uc(t)i(t)=Cdtduc(t)ur(t)=LCdt2d2uc(t)+RCdtduc(t)+uc(t)
整理得：
d
2
u
c
(
t
)
d
t
2
+
R
L
d
u
c
(
t
)
d
t
+
1
L
C
u
c
(
t
)
=
1
L
C
frac{d^2u_c(t)}{dt^2}+frac{R}{L}frac{du_c(t)}{dt}+frac{1}{LC}u_c(t)=frac{1}{LC}
dt2d2uc(t)+LRdtduc(t)+LC1uc(t)=LC1
拉普拉斯变换
为什么引入拉普拉斯变换？
在自控这门课中，用的最多的自然就是传递函数，谈及传递函数，一个绕不开的一个概念就是：拉普拉斯变换，对于它，我们首先要知道为什么要用到它，这其中有两个原因：
①对于一个系统，如果建立了微分方程，在进行分析时，自然是求解其微分方程，但是过程麻烦，很耗时，所以另辟蹊径。那就是先对微分方程进行拉氏变换得到代数方程，代数方程就很易求解了，对结果再进行拉氏反变换，就可以间接得到微分方程的解。
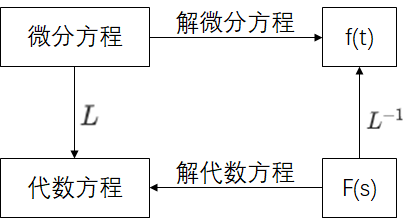
②可以用拉氏变换定义复域数学模型——传递函数，这是使用它的一个更重要的原因。
常见拉氏变换表
直接背会即可，不必采用拉氏变换的几种定理自行证明
使用拉氏变换求解微分方程
此处我们举一个微分方程使用拉氏变求解系统的传递函数的例子
{
y
′
′
(
t
)
+
a
1
⋅
y
′
+
a
2
⋅
y
(
t
)
=
1
(
t
)
y
(
0
)
=
y
′
=
0
begin{cases} y^{''}(t)+a_1·y^{'}+a_2·y(t)=1(t) \ y(0)=y^{'}=0 end{cases}
{y′′(t)+a1⋅y′+a2⋅y(t)=1(t)y(0)=y′=0
进行
L
L
L变换
(
S
2
+
a
1
S
+
a
2
)
⋅
Y
(
S
)
=
1
S
(S^2+a_1S+a_2)·Y(S)=frac{1}{S}
(S2+a1S+a2)⋅Y(S)=S1
整理得
Y
(
S
)
=
1
S
(
S
2
+
a
1
S
+
a
2
)
R
(
S
)
=
1
S
Y
(
S
)
R
(
S
)
=
1
S
2
+
a
1
S
+
a
2
Y(S)=frac{1}{S(S^2+a_1S+a_2)}\ R(S)=frac{1}{S}\ frac{Y(S)}{R(S)}=frac{1}{S^2+a_1S+a_2}
Y(S)=S(S2+a1S+a2)1R(S)=S1R(S)Y(S)=S2+a1S+a21
拉氏变换
这里附上题目，对拉氏变换进行题目求解
拉氏反变换
拉氏反变换是重点内容，这里只需要掌握一个公式即可，就是留数法。留数法一般结合查表法使用，因此把一些常用的函数的拉氏变换熟练掌握是十分必要的。
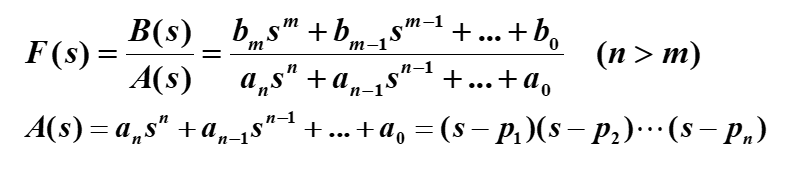
题型一：A(s)=0无重根
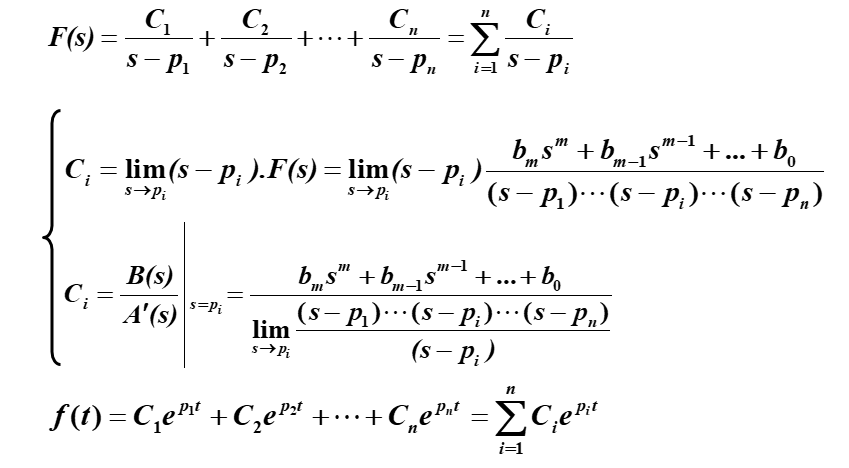
【例题】
【练习】
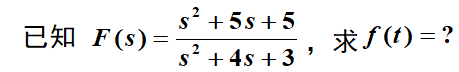
题型二：A(s)=0有重根
【例题】
传递函数
在零初始条件下，线性定常系统输出量拉氏变换与输入量拉氏变换之比。
G ( s ) = C ( s ) R ( s ) G(s)=frac{C(s)}{R(s)} G(s)=R(s)C(s)
传递函数的标准函数
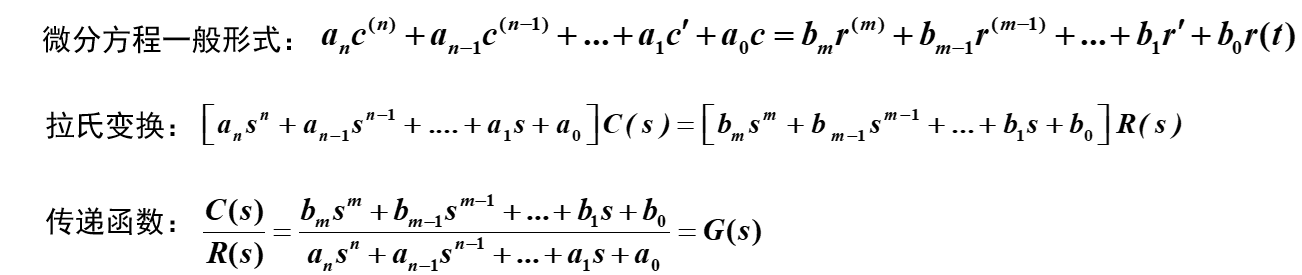
传递函数的两种形式
【例题】
传递函数的性质
传递函数的局限性
（1）原则上不反映非零初始条件时系统响应的全部信息；
（2）适合于描述单输入/单输出系统；
（3）只能用于表示线性定常系统。
典型环节的传递函数
| 序号 | 环节名称 | 微分方程 | 传递函数 | 举例 |
|---|---|---|---|---|
| 1 | 比例环节 | c = K ⋅ r c = K·r c=K⋅r | K K K | 电位器，放大器，自整角机 |
| 2 | 惯性环节 | T c ˙ + c = r Tdot{c}+c=r Tc˙+c=r | 1 T s + 1 frac{1}{Ts+1} Ts+11 | CR电路，交、直流电动机 |
| 3 | 振荡环节 | T 2 c ¨ + 2 ξ T c ˙ + c = r ( 0 < ξ < 1 ) T^2ddot{c}+2{xi}Tdot{c}+c=r\(0<xi<1) T2c¨+2ξTc˙+c=r(0<ξ<1) | 1 T 2 s 2 + 2 ξ T s + 1 frac{1}{T^2s^2+2{xi}Ts+1} T2s2+2ξTs+11 | R-L-C电路,弹簧质块阻尼器系统 |
| 4 | 积分环节 | c ˙ = r dot{c}=r c˙=r | 1 s frac{1}{s} s1 | 水箱( 流量Q—液位h ) |
| 5 | 微分环节 | c = r c=r c=r | s s s | |
| 6 | 一阶复合微分环节 | c = τ r ˙ + r c={tau}dot{r}+r c=τr˙+r | τ s + 1 {tau}s+1 τs+1 | |
| 7 | 二阶复合微分环节 | c = τ 2 r ¨ + 2 τ ξ r ˙ + r c={tau}^2ddot{r}+2{tau}{xi}dot{r}+r c=τ2r¨+2τξr˙+r | τ 2 s 2 + 2 τ ξ s + 1 {tau}^2s^2+2{tau}{xi}s+1 τ2s2+2τξs+1 |
综合题目讲解
课后习题
下节课知识预备
方框图及其化简
结构图等效变换规则
最后
以上就是故意发卡为你收集整理的第二节 控制系统的数学模型——传递函数博客已搬家，欢迎访问新居：http://lukeyalvin.site，主要涉及SLAM相关方向，目前知识积累尚浅，多多指教！第二节 控制系统的数学模型——传递函数的全部内容，希望文章能够帮你解决第二节 控制系统的数学模型——传递函数博客已搬家，欢迎访问新居：http://lukeyalvin.site，主要涉及SLAM相关方向，目前知识积累尚浅，多多指教！第二节 控制系统的数学模型——传递函数所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
![matlab 由状态空间表达式求传递函数 [李园7舍_404]1 内容2 求解](/uploads/reation/bcimg5.png)
发表评论 取消回复