数字信号上下采样对频谱影响，以及如何添加相应滤波器

为了便于理解，我们不妨假设有这样一个低通信号，他的数据速率（即当前采样率Fs）为1GHz，不过最高频率fm只有300M。
$$x[n]<--->X(e^{j\omega })$$
该信号的时域波形如何我们并不关心，因为上下采无非就是往中间插0以及从内部抽取。我们关心他的频域如何变化，会不会混叠，以及我们上下采样之前之后应当如何添加相应的低通滤波器。
假设现在频谱如下所示

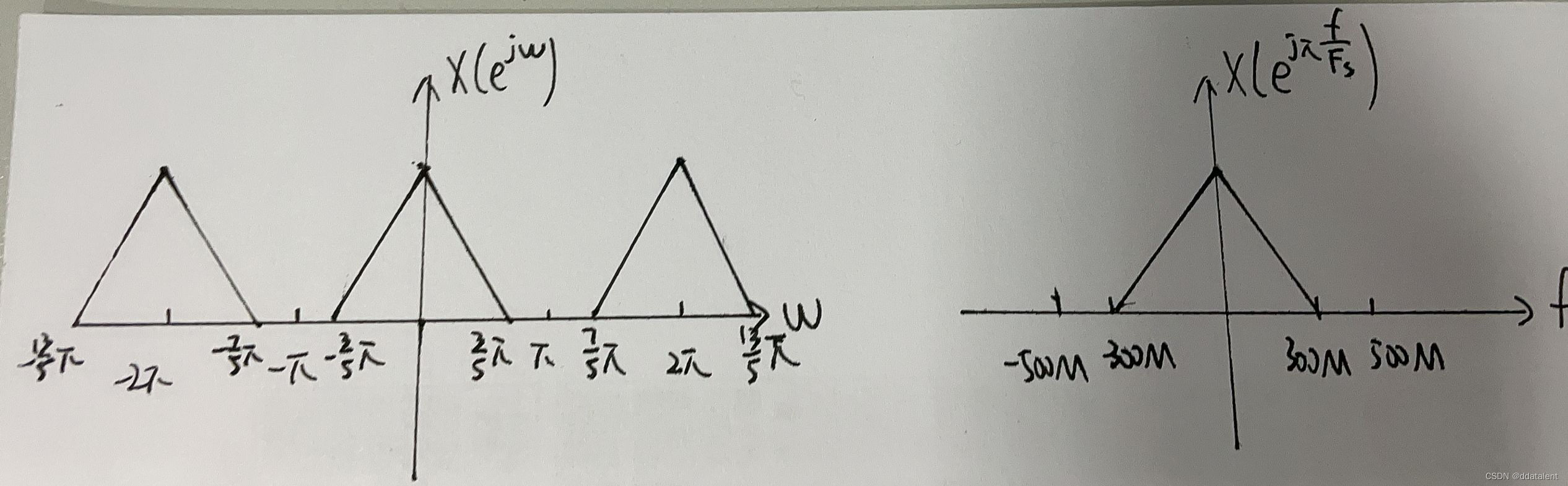
左图为该离散信号的频谱，离散信号的频谱以2$\pi$为周期延拓。
右图为matlab中对该信号进行观测所得频谱，更便于大家理解。受限于奈奎斯特采样定律，只能观察$[-Fs/2,Fs/2]$频段内频谱。

这两张图其实是统一的，右图中横坐标的$Fs/2=500M$对应着左图横坐标的$\pi$。
我们时时刻刻牢记这一点，接下来频谱的变化我们都将用左图的形式表现，对应的方便理解的右图的形式，大家只需要替换 $\pi <-->F_s/2$即可。$F_s$是当前时刻采样率。

1.上采样（整数倍内插）

我们首先尝试对该信号进行$I$倍上采样，也就是往两个相邻信号中间插$I-1$个 0。
$$x_I[n]=\{\begin{array}{ll}x[\frac{n}{I}]& \text{if }n=0,I,2I,...\\ 0& \text{else}\end{array}$$
则频域变化为（省去推导过程）
$$X_I(e^{j\omega })=X(e^{j\omega I})$$
由该式我们可以知道，内插后的频谱是原频谱的线性收缩。
为便于画图，我们假设此时是上两倍采样（即$I=2$），则相应的频谱变化为

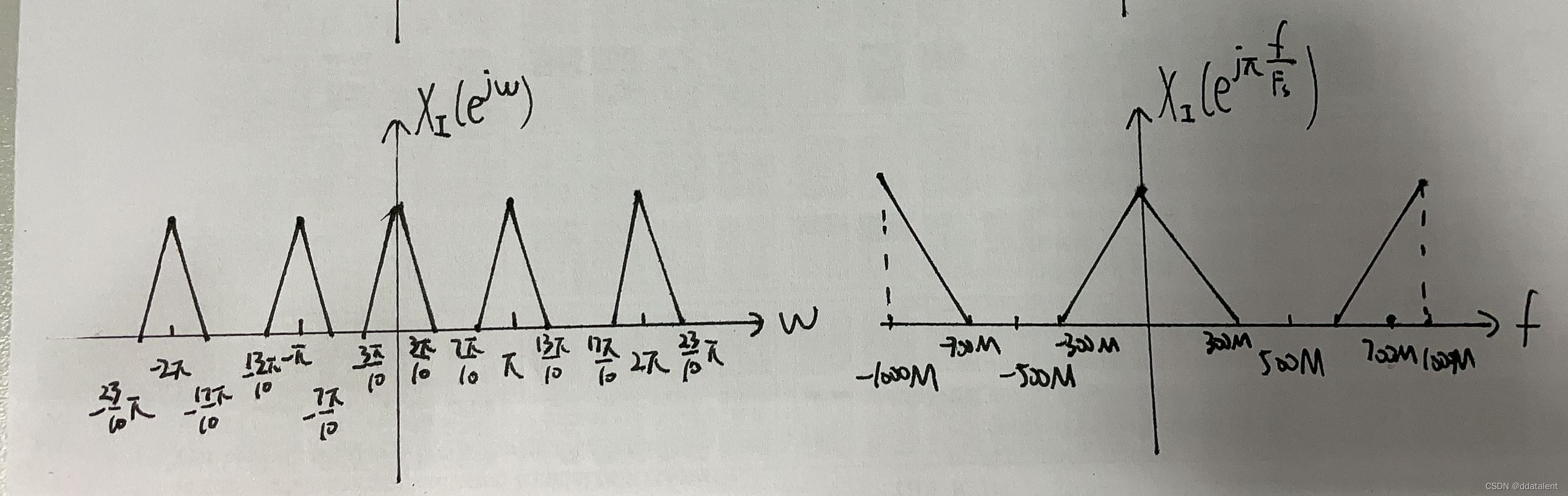
左图就是线性收缩后的频谱，就是内插后信号的频谱。
此时采样率变为原信号的两倍，新的$F_s=2000M$，最大观察频点为1000M，带入上文着重强调的公式$$\pi <-->F_s/2=1000M$$得到便于观察的频谱如右图所示。

此时，我们就会观察到原来在±1000M频点附近的高频分量，相当于我们的信号突然多出了很多不必要的高频噪声，因此我们需要添加一个低通滤波器进行滤除。
滤波器只需要保证通带截止频率>300M，阻带截止频率＜700M，即可。

2.下采样（整数倍抽取）

然后我们尝试对原信号进行下采样，就是把原始采样序列x[n] 每隔(D-1) 个数据取一个，以形成一个采样率为原序列1/D的新序列$x_D(m)$为：
$$x_D[n]=x[Dn]$$

省去推导过程，频域变化为：

$$X_D(e^{j\omega })=\frac{1}{D}\sum _{l=0}^{D-1}X[e^{j(\omega -2\pi l)/D}]$$

仔细观察该公式，发现和上采样单纯的线性收缩不同，下采样并不是单纯将频谱线性展宽。

下采样后的频谱为原频谱经频移和D倍展宽后的D个频谱的叠加和，因此可能存在混叠。

为方便大家理解，我们对该信号进行两倍下采样，得到频谱变化如下图所示：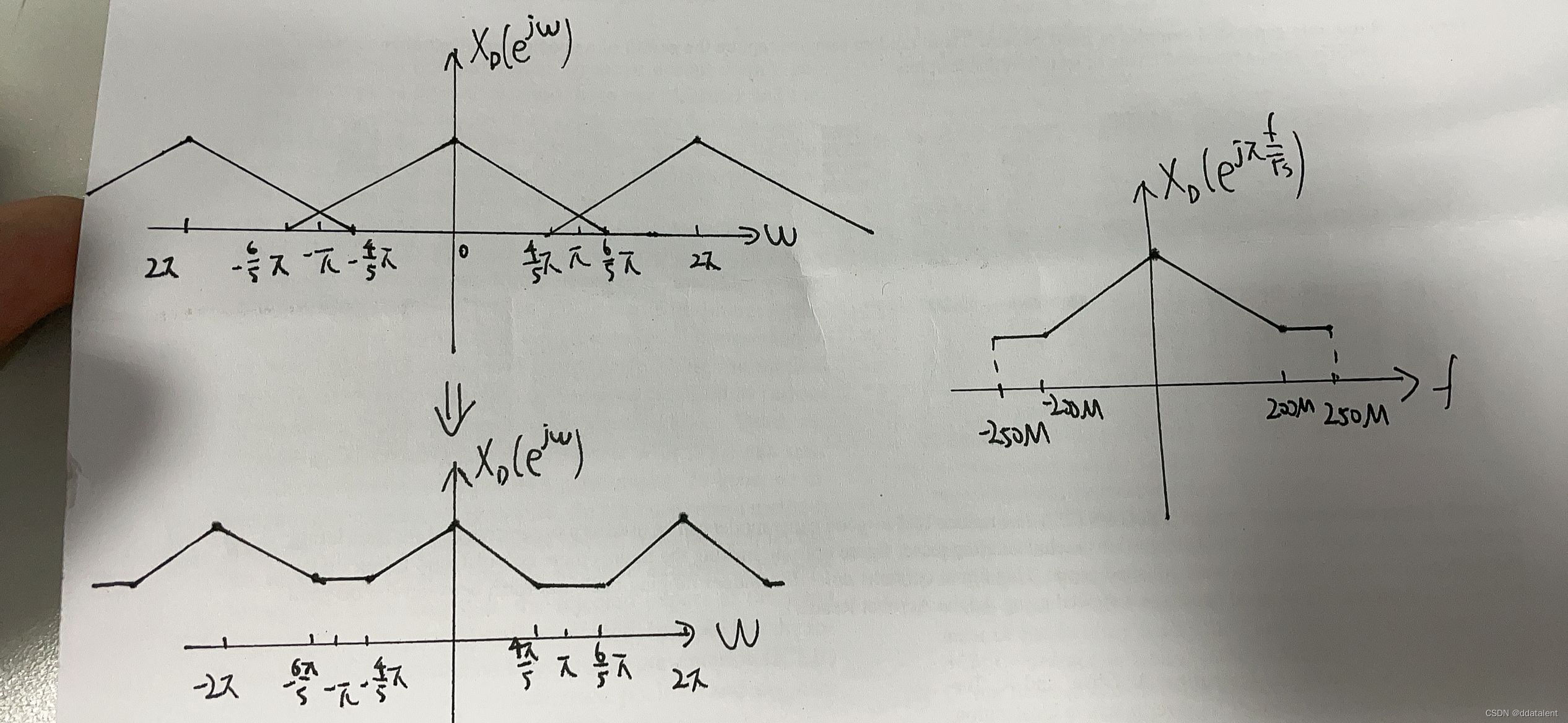

因此，下采样之前需要进行防混迭滤波。
我们可以用一个截止频率为$-\pi /D$的滤波器

这样就可以有效防止混叠。

综上，上采是先内插，再滤波。下采是先滤波，再抽取。

reference:

1. 奥本海姆 《信号与系统》
2. 沈莹 《软件无线电》

最后

以上就是淡然白云为你收集整理的数字信号上下采样对频谱影响，以及如何添加相应滤波器的全部内容，希望文章能够帮你解决数字信号上下采样对频谱影响，以及如何添加相应滤波器所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。