利用matlab实现北斗RNSS单点定位解算

说实话，只要是了解导航的朋友们都知道RNSS单点定位的原理是比较简单的，从几何原理分析，只需要3颗卫星（三球交汇嘛）就能确定用户接收机天线的位置。
但由于卫星钟和接收机中两者内的钟难以保持严格同步，实际观测的接收机至卫星之间的距离均含有卫星钟和接收机钟不同步的影响。对于卫星钟差，可以应用导航电文中给出的钟差修正参数进行改正；对于接收机钟差，一般难以预先准确地确定。所以在实际应用中常把接收机钟差和接收机天线的位置一并作为未知量，这样求解四个未知参数需要四个观测量，即接收机需同时观测至少4颗卫星。但从其原理到实现还有一段路要走，下面我浅谈一下我对于编写相应程序的理解。对于基本流程不是特别清晰的还可以参考这篇文章

（不太会用LaTeX，干脆直接贴图）

1.读取数据及初始化

首先还是读取数据和设定好相关参数，其中所用到的read_Ofile函数是我自己定义的主要用于读取观测文件的一个函数，由于大家读取的方式可能有所不同，我在这不过多赘述，其读取所得结果分别为t_R（钟面时）、sat_num（该历元下接收到北斗卫星信号的卫星数目）、PRN（卫星号）、PR（伪距）

clc;
clear;
close;

% 1.读取数据
%1.1 读取观测文件数据
data_fre1 = fopen('WUH200CHN_R_20210060000_01D_30S_MO_Observations1.txt','r');
% data_fre3=importdata('WUH200CHN_R_20210060000_01D_30S_MO_Observations3.txt');
[t_R,sat_num,PRN,PR] = read_Ofile(data_fre1);     %通过自编写函数实现对数据的有效读取

%1.2 读取星历文件数据
Data_bro=importdata("Nfile-new.csv");
Broad_eph=Data_bro.data;

% 2.设定解算过程中所用常数
c = 2.99792458e8;
omegaDote = 7.2921150e-5;
flag=1;      %绘制动图开关

% 3.给定待定点的近似坐标和初始接收机钟差
% x0 = -2267749.0000;
% y0 = 5009154.0000;
% z0 = 3221290.0000;
x0=0;
y0=0;
z0=0;
delta_tR=0;
corrdinate_r=[-2267749.0000,5009154.0000,3221290.0000];   %由观测文件中读取到的近似点

2.解算主体过程

然后就是按照上诉流程来进行迭代计算，基本可以看成是以下4个步骤
（1）迭代计算出收敛的信号传播时间
（2）遍历同一历元下的所有卫星计算出其传播时间，并解算传播时间过程中得到的中间量来计算方向余弦，构造出法方程，解算得到改正量也即得到了接收机的近似位置和接收机钟差
（3）解算出的接收机的近似位置并不能看作解算结果，需要继续迭代，直至前后两次迭代的三维坐标之差绝对值中的最小值满足条件时，所得的解算结果才可看作为接收机的位置（由于钟差较小且较稳定，所以并不对钟差做限定）
（4）遍历历元得到不同历元下接收机的位置坐标和钟差

% 4.计算信号传播时间并据此得到接收机位置(迭代计算)
for i=1:size(sat_num)             %时间遍历
    a=zeros(sat_num(i),3);
    l=zeros(sat_num(i),1);
    corrdinate0(i,:)=[x0,y0,z0];       
    corrdinate1(i,:)=ones(1,3);
    while min(abs(corrdinate0(i,:)-corrdinate1(i,:)))>0.01
        corrdinate0(i,:)=corrdinate1(i,:);
        for j=1:sat_num(i)            %同一历元下的卫星遍历
            %prn-->卫星号 t0-->信号接收时刻的接收机钟面时 rhoS-->伪距观测值
            prn=PRN(i,j);   t0=t_R(i);   rhoS=PR(i,j);
            x=corrdinate0(i,1);   y=corrdinate0(i,2);   z=corrdinate0(i,3);
            broadEph_tar = select_eph(t0,prn,Broad_eph);   %找到对应的星历
            
            %计算得到信号传播时间并输出卫星在信号接收时刻时的BDCS下的位置及距离
            toc=broadEph_tar(3);        %周内秒
            delta_tS = broadEph_tar(4)+broadEph_tar(5)*(t0-toc)+broadEph_tar(6)*(t0-toc)^2;   %由星历计算出卫星钟差
            %信号传播时间收敛
            [tau_S1(j),x_S1(j),y_S1(j),z_S1(j),R_S(j)]=cal_SignalPropagationTime(rhoS,broadEph_tar,delta_tR,t0,x,y,z);
            
            %计算方向余弦a1,a2,a3
            a(j,1)=(x_S1(j)-x)/R_S(j);
            a(j,2)=(y_S1(j)-y)/R_S(j);
            a(j,3)=(z_S1(j)-z)/R_S(j);
            l(j)=R_S(j)-rhoS-c*delta_tS+c*delta_tR;
        end
        
        %计算法方程得到改正数(也可通过对法方程更新实现求解)
        A=[a,-ones(sat_num(i),1)];
        N=A'*A;
        U=A'*l;
        delta_X=NU;     %delta_X为改正数
        
        %对初值进行更改并保留(delta_X的四项分别为Δx、Δy、Δz、c*ΔtR)
        x=x+delta_X(1);
        y=y+delta_X(2);
        z=z+delta_X(3);
        corrdinate1(i,1)=x;    corrdinate1(i,2)=y;   corrdinate1(i,3)=z;
        delta_tR=delta_tR+delta_X(4)/c;   %对接收机钟差进行改正时要除以光速c
        clc_err(i)=delta_tR;
    end
end

其中非常重要的一个函数就是cal_SignalPropagationTime函数，故名思意即为解算出信号传播时间的函数，它完成了第一层循环的要求。在它里面我也调用了一些自己编写的函数，像cal_coordinate函数（用于计算卫星位置），它们都在我之前的文章中提及过，cal_SignalPropagationTime函数的代码如下：

function [tau_S1,x_S1,y_S1,z_S1,R_S] = cal_SignalPropagationTime(rhoS,broadEph_tar,delta_tR,t_R,x0,y0,z0)
% function:
%   迭代计算出计算信号传播时间

% input:
%   rhoS-->对应卫星的伪距观测值
%   delta_tR-->接收机钟差初始近似值
%   t_R-->信号接收时刻接收机的钟面时
%   x0、y0、z0-->待定点近似坐标
% output:
%   tau_S1-->信号传播时间
%   x_S1、y_S1、z_S1-->信号发射时刻卫星在信号接收时刻时的BDCS下的位置
%   R_S-->卫星和待定近似点的距离

% 所需常数
c = 2.99792458e8;
omegaDote = 7.2921150e-5;

% 1.给定信号传播时间初始值
toc=broadEph_tar(3);        %周内秒
delta_tS = broadEph_tar(4)+broadEph_tar(5)*(t_R-toc)+broadEph_tar(6)*(t_R-toc)^2;   %由星历计算出卫星钟差
tau_S=0;
tau_S1 = rhoS/c - delta_tR +  delta_tS;
while abs(tau_S-tau_S1)>0.0001/c     %传播时间收敛误差为对应的距离为1cm
    tau_S=tau_S1;
    % 2.计算信号发射时间
    T_R=t_R-delta_tR;       %信号接受时刻钟面时
    T_S=T_R-tau_S;          %信号发射时刻
    
    % 3.计算卫星在发射时刻BDCS下的位置
    [x_S,y_S,z_S]=cal_coordinate(T_S,broadEph_tar);
    
    % 4.计算信号发射时刻卫星在信号接收时刻时的BDCS下的位置
    dleta_alpha=omegaDote*tau_S;    %坐标系旋转角度
    x_S1=[cos(dleta_alpha) sin(dleta_alpha) 0]*[x_S,y_S,z_S]';
    y_S1=[-sin(dleta_alpha) cos(dleta_alpha) 0]*[x_S,y_S,z_S]';
    z_S1=z_S;
    
    % 5.重新计算信号传播时间
    R_S=sqrt((x_S1-x0)^2+(y_S1-y0)^2+(z_S1-z0)^2);    %卫星和待定近似点的距离
    tau_S1=R_S/c;
end
delta=tau_S-tau_S1;    %计算两者的差值用于校验
end

3.将结果绘图

最后是将解算出来的结果绘制出图像，包括由接收机三维坐标所构成的散点图、三维坐标误差图及接收机钟差与其均值的差值图

% 5.绘制坐标收敛结果
figure(1);
gap=30;                     %由于观测历元较多,每相隔gap个数绘制一个点
Length=length(corrdinate1);
hold on;    grid on;   axis auto;
scatter3(corrdinate_r(1),corrdinate_r(2),corrdinate_r(3),'o','b');
% scatter3(corrdinate1(end,1),corrdinate1(end,2),corrdinate1(end,3),'o','b');
plot3(corrdinate1(1:gap:Length,1),corrdinate1(1:gap:Length,2),corrdinate1(1:gap:Length,3),'--o');
text(corrdinate_r(1),corrdinate_r(2),corrdinate_r(3),'近似点');
% for i=1:gap:Length
%     text(corrdinate1(i,1),corrdinate1(i,2),corrdinate1(i,3),num2str(i));
% end
%绘制动图
if flag==1
    at = animatedline('Color','b','Marker','*','MarkerSize',3);
    Mo=moviein(length(corrdinate1)/100);
    for k=1:gap:Length
        addpoints(at,corrdinate1(k,1),corrdinate1(k,2),corrdinate1(k,3));
        Mo(k)=getframe;
    end
    drawnow;
    movie(Mo,1,1);
end

% 6.绘制误差图像
figure(2);
hold on;    grid on;
if corrdinate0(1)==0            %如果初始值设为0则剔除变化量较大的前几个值
    plot(1:length(sat_num)-3,corrdinate1(4:end,1)-corrdinate_r(1));
    plot(1:length(sat_num)-3,corrdinate1(4:end,2)-corrdinate_r(2));
    plot(1:length(sat_num)-3,corrdinate1(4:end,3)-corrdinate_r(3));
else
    plot(1:length(sat_num),corrdinate1(:,1)-corrdinate_r(1));
    plot(1:length(sat_num),corrdinate1(:,2)-corrdinate_r(2));
    plot(1:length(sat_num),corrdinate1(:,3)-corrdinate_r(3));
end
legend("X坐标误差","Y坐标误差","Z坐标误差");
ylabel("误差大小(m)");

figure(3);
plot(1:length(sat_num),clc_err(:)-mean(clc_err));  grid on;
title("钟差与均值之差");

图1 接收机三维坐标散点图

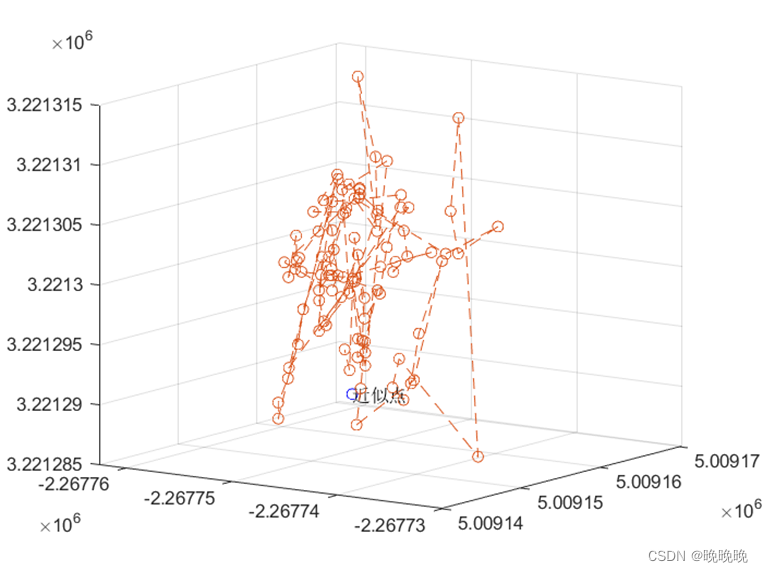
图2 三维坐标误差图

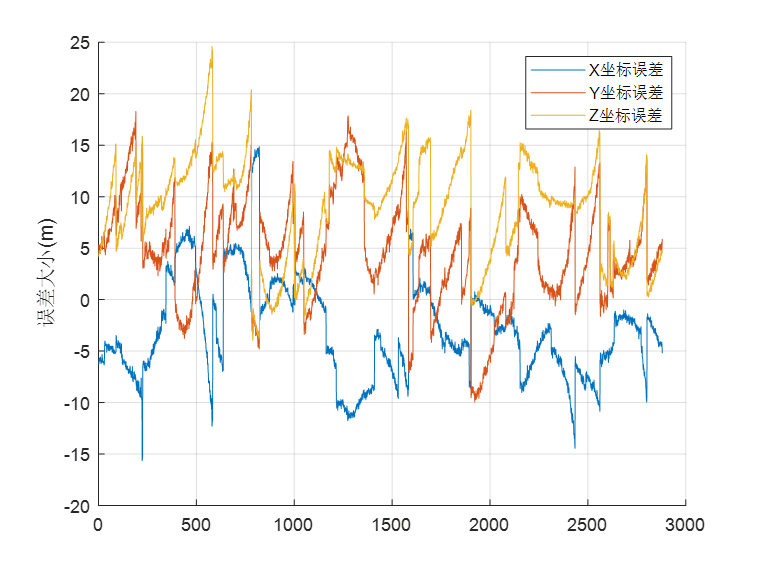
图3 接收机钟差与其均值的差值图

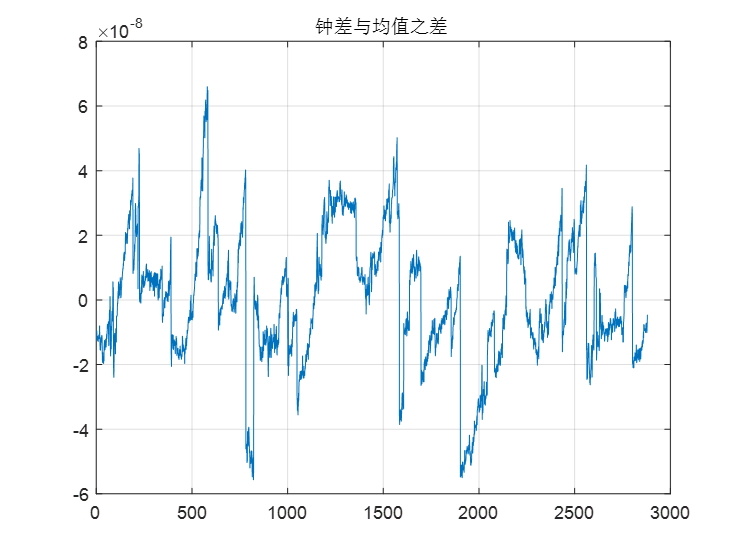
希望觉得有所帮助的朋友能点赞支持一下！

最后

以上就是愤怒西牛为你收集整理的利用matlab实现北斗RNSS单点定位解算的全部内容，希望文章能够帮你解决利用matlab实现北斗RNSS单点定位解算所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。