常见算法
- 动态规划-后一个状态能由前一个状态转换来
- 分治
- 回溯
- 并查集 - 算是否关联
- 前序遍历（先序遍历）
- 中序遍历
- 双指针（快慢指针）
- 从集合中选择满足条件的结果(去重或不去重)
- 快速选择 - 求第K大(小)元素或前K大(小)元素
- 二分查找
- 最小(大)堆，求有序的前K个元素
- 单调栈-划分区间求极致值
- 出度（两端烧绳子求中点，无向图求中点）
- 多源广度(深度)优先搜索
- 求一个集合(数组) 符合某种条件的(真)子集
动态规划-后一个状态能由前一个状态转换来
动态规划的关键是推导状态转移方程，常用来解决后一个状态能由前一个状态得出的场景。
面试题 17.09 ：有些数的素因子只有 3，5，7，请设计一个算法找出第 k个数。注意，不是必须有这些素因子，而是必须不包含其他的素因子。例如，前几个数按顺序应该是 1，3，5，7，9，15，21。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/get-kth-magic-number-lcci
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution { public int getKthMagicNumber(int k) { int[] rArr = new int[k]; rArr[0] = 1; int n = 1; int index1 = 0; int index2 = 0; int index3 = 0; while(n != k) { int val1 = rArr[index1] * 3; int val2 = rArr[index2] * 5; int val3 = rArr[index3] * 7; int min = Math.min(Math.min(val1, val2),val3); if(min == val1) index1++; if(min == val2) index2++; if(min == val3) index3++; rArr[n] = min; n++; } return rArr[k-1]; } }
分治
采用分治法解决的问题一般具有的特征如下：
- 问题的规模缩小到一定的规模就可以较容易地解决。
- 问题可以分解为若干个规模较小的模式相同的子问题，即该问题具有最优子结构性质。
- 合并问题分解出的子问题的解可以得到问题的解。
- 问题所分解出的各个子问题之间是独立的，即子问题之间不存在公共的子问题。
设计步骤
- 划分步：把输入的问题划分为k个子问题，并尽量使这k个子问题的规模大致相同。
- 治理步：当问题的规模大于某个预定的阈值n0时，治理步由k个递归调用组成。
- 组合步：组合步把各个子问题的解组合起来，它对分治算法的实际性能至关重要，算法的有效性很大地依赖于组合步的实现。
分治法的关键是算法的组合步。究竟应该怎样合并，没有统一的模式，因此需要对具体问题进行具体分析，以得出比较好的合并算法。
如计算大整数乘积：我们可以将大整数对拆为两个部分。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32即a和b相乘就可以写为：a * b = { a1 * 10^(n1/2) + a0 } * { b1 * 10^(n2/2) + b0 } 展开后整理得： a * b = a1*b1 * 10^[ (n1+n2)/2 ] + a1*b0 * 10^(n1/2) + a0*b1 * 10^(n2/2) + a0*b0 ； 实现方法：我们定义一个支持方法f(char *a,char *b)，用于在结束递归时（在本例中，我定义有一个数是1位时结束递归， 直接用普通乘法）计算两个字符串的乘积（为了表示大数，用字符串来接受参数）。 有了这个支持方法，分治递归实现两个大数乘法 int f(char *a,char *b)//用字符串读入2个大整数 { long result = 0; if(len(a) == 1 || len == 1) //递归结束的条件 result = f(a,b); else //如果2个字符串的长度都 >= 2 { char *a1 =a; *(a1+(len(a)/2))=''; //截取前一半的字符串(较短的一半) char *a0 = a+len(a)/2; //截取后一半的字符串 *(a0+len(a)/2)=''; char *b1=b; *(b1+(len(a)/2))=''; //截取前一半的字符串(较短的一半) char *b0 = a+len(a)/2; //截取后一半的字符串 *(b0+len(b)/2)=''; //分治的思想将整数写成这样： a = a1 * 10^(n1/2) + a0, b = b1 * 10^(n2/2)，相乘展开得到以下四项 //其中n1，n2为2个整数a，b的位数 result = (f(a1,b1) * pow(10,len( a0) + len(b0)) + f(a1,b0) * pow(10, len(a0) +f(a0,b1) * pow(10,len(b0)) + fy(a0,b0)); } return result; }
大整数乘积部分来源：大整数乘积
回溯
回溯算法也叫试探法，它是一种系统地搜索问题的解的方法。主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。
用回溯算法解决问题的一般步骤：
- 针对所给问题，定义问题的解空间，它至少包含问题的一个（最优）解。
- 确定易于搜索的解空间结构,使得能用回溯法方便地搜索整个解空间 。
- 以深度优先的方式搜索解空间，并且在搜索过程中用剪枝函数避免无效搜索。
下面是经典的回溯 八皇后的进阶 N皇后：
面试题 08.12. 八皇后：设计一种算法，打印 N 皇后在 N × N棋盘上的各种摆法，其中每个皇后都不同行、不同列，也不在对角线上。这里的“对角线”指的是所有的对角线，不只是平分整个棋盘的那两条对角线。
注意：本题相对原题做了扩展
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/eight-queens-lcci
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79class Solution { public List<List<String>> solveNQueens(int n) { List<List<String>> ans = new ArrayList(); int[][] c = new int[n][n]; dfs(c,0,0,n,n,ans); return ans; } public void dfs(int[][] c, int i, int j, int n, int surNum, List<List<String>> ans) { while(j < n) { // 一行就行了,因为任何一行不放，那就不会有结果 if(isYes(c, i, j, n)) { c[i][j] = 1; surNum--; if(surNum == 0) { addT(c, ans); c[i][j] = 0; // 即使是成功的,走之前也要回溯 return; } dfs(c, i+1, 0, n, surNum,ans); surNum++; // 这里回溯 c[i][j] = 0; } j++; } } public boolean isYes(int[][] c, int i, int j, int n){ // 注释掉的判断都是不需要的，只需要判断上面的就行，同一行和下面的都不用判断，因为上面的逻辑，一旦放了就直接去下一行了，当前行不会放，然后下面的总是后放的，所以放的点下面肯定是没有的 // for(int x = 0; x < n; x++) { // if(c[i][x] == 1) return false; // } // for(int x = 0; x < n; x++) { // if(c[x][j] == 1) return false; // } // for(int x = i+1,y=j+1; x<n&&y<n; ) { // if(c[x][y] == 1) return false; // x++; // y++; // } for(int x = i-1; x >= 0; x--) { if(c[x][j] == 1) return false; } for(int x = i-1,y=j-1; x>=0&&y>=0; ) { if(c[x][y] == 1) return false; x--; y--; } for(int x = i-1,y=j+1; x>=0&&y<n; ) { if(c[x][y] == 1) return false; x--; y++; } // for(int x = i+1,y=j-1; x<n&&y>=0; ) { // if(c[x][y] == 1) return false; // x++; // y--; // } return true; } public void addT(int[][] c, List<List<String>> ans) { List<String> e = new ArrayList(); for(int i=0; i< c.length; i++) { StringBuffer s = new StringBuffer(); for(int x : c[i]) { if(x == 1) { s.append("Q"); } else { s.append("."); } } e.add(s.toString()); } ans.add(e); } }
并查集 - 算是否关联
并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受；即使在空间上勉强通过，运行的时间复杂度也极高。
并查集常用来解决集合和集合之前的关系判断。判断一个关系链接中有多少个不相连的结合，在一个关系范围内A和B是否有关系。
547:省份数量 有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c直接相连，那么城市 a 与城市 c 间接相连。 省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。 给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而
isConnected[i][j] = 0 表示二者不直接相连。 返回矩阵中 省份 的数量。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/number-of-provinces
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42/*关键在于union维护关系，finPar寻找关系*/ class Solution { public int findCircleNum(int[][] isConnected) { int cityNum= isConnected.length; if(0 == cityNum) return 0; int[] cityPar = new int[cityNum]; for(int i = 0; i < cityNum; i ++) { cityPar[i] = i; } for(int i = 0; i< cityNum; i ++) { for(int j = i+1; j< cityNum; j ++) { if(isConnected[i][j] == 0) continue; union(cityPar, i, j); } } HashSet<Integer> allPar = new HashSet(); for(int i = 0; i < cityNum; i ++) { allPar.add(finPar(cityPar,i)); } return allPar.size(); } public void union(int[] cityPar, int i, int j) { int iPar = finPar(cityPar,i); int jPar = finPar(cityPar,j); if(iPar == jPar) return; if(iPar < jPar) { cityPar[jPar] = iPar; } else { cityPar[iPar] = jPar; } } public int finPar(int[] cityPar, int i) { while(cityPar[i] != i) { i = cityPar[i]; } return i; } }
前序遍历（先序遍历）
先序遍历(Pre-order)，按照根左右的顺序沿一定路径经过路径上所有的结点。在二叉树中，先根后左再右。巧记：根左右。
先序遍历的实现：
1
2
3
4
5
6
7
8
9
10
11
12
13public void flatten(TreeNode root) { Deque<TreeNode> stock = new ArrayDeque(); while(!stock.isEmpty() || root != null) { while(root != null) { stock.push(root); // 这里读root的值 root = root.left; } root = stock.pop(); root = root.right; } }
中序遍历
中序遍历（LDR）是二叉树遍历的一种，也叫做中根遍历、中序周游。在二叉树中，中序遍历首先遍历左子树，然后访问根结点，最后遍历右子树。
1
2
3
4
5
6
7
8
9
10
11Deque<TreeNode> stock = new ArrayDeque(); while(!stock.isEmpty() || root != null) { while(root != null) { stock.push(root); root = root.left; } root = stock.pop(); // 这里读root的值 root = root.right; }
双指针（快慢指针）
常用来解决数组问题，用双指针避免多次遍历。
31: 下一个排列 实现获取 下一个排列 的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列（即，组合出下一个更大的整数）。如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。必须 原地 修改，只允许使用额外常数空间。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/next-permutation
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49class Solution { public void nextPermutation(int[] nums) { if(nums.length == 0) return; // 范围在0到nums.length - 1找 if(!nextPermutation(nums, 0, nums.length - 1)) // 如果没找到，直接反转就行了 reserve(nums, 0, nums.length-1); } boolean nextPermutation(int[] nums,int start, int end) { int slow = end; while (slow > start) { int fast = slow - 1; while (fast >= start) { // 小于的情况 if(nums[fast] < nums[slow]) { // 两个值不挨着的话，那么区间内，也就是fast到end这块可能还有能交换的，尝试找一下 if(slow - fast > 1 && nextPermutation(nums, fast+1, end)){ return true; } // 交换 sweep(nums, slow, fast); // 反转 reserve(nums, fast+1, nums.length-1); return true; } else if (nums[fast] == nums[slow] && slow - fast > 1) { // 尝试找一个，找到就结速，找不到就继续移动 if(nextPermutation(nums, fast+1, slow)) return true; } fast--; } slow--; } return false; } void sweep(int[] nums, int i, int j) { int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; } void reserve(int[] nums, int start, int end){ while(start<end) { sweep(nums, start, end); start++; end--; } } }
从集合中选择满足条件的结果(去重或不去重)
如果从一个集合内选择合适的元素来达成某个条件，要求结果集不能重复。此时简单的遍历和结果集判重就很麻烦，一个好的方法是先对集合内的元素排序，这样选中一个元素后就能一次性跳过，避免了去重流程。
例如：15. 三数之和 给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0？请你找出所有和为 0 且不重复的三元组。
注意：答案中不可以包含重复的三元组。
来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/3sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32class Solution { public List<List<Integer>> threeSum(int[] nums) { List<List<Integer>> endRes = new ArrayList<>(); Arrays.sort(nums); int l = nums.length; for(int i = 0; i < l -2; i++) { if(i>0 && nums[i] == nums[i-1]) continue; int j = i+1; int k = l-1; int target = - nums[i]; while(k > j) { int neSum = nums[j] + nums[k]; if(neSum == target) { List<Integer> res = new ArrayList<>(); res.add(nums[i]); res.add(nums[j]); res.add(nums[k]); endRes.add(res); while (++j<k && nums[j] == nums[j-1]); while (--k>j && nums[k] == nums[k+1]); } else if(neSum < target) { while (++j<k && nums[j] == nums[j-1]); } else { while (--k>j && nums[k] == nums[k+1]); } } } return endRes; } }
上面这个题目还不够经典，更经典的是47. 全排列 II和40. 组合总和 II，想通：集合重复的本质是相同元素不同顺序的排列导致的，如果相同元素严格按照顺序取用，就不会有重复现象了。这个就能明白这个道理了。
- 全排列 II - 这一题是排列不重复即可
给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class Solution { List<List<Integer>> ans = new ArrayList<>(); boolean[] visit; public List<List<Integer>> permuteUnique(int[] nums) { Arrays.sort(nums); visit = new boolean[nums.length]; dfs(new ArrayList<>(), nums, 0); return ans; } void dfs(List<Integer> cur, int[] nums, int no) { if(no == nums.length) { ans.add(copyList(cur)); return; } for(int i = 0; i < nums.length; i++) { // 这一步是关键,如果不按顺序取就结束 if(visit[i] || (i>0 && nums[i] == nums[i-1] && !visit[i-1])) continue; cur.add(nums[i]); visit[i] = true; dfs(cur, nums, no+1); cur.remove(cur.size()-1); visit[i] = false; } } List<Integer> copyList(List<Integer> total) { List<Integer> copyList = new ArrayList<>(); for(int i = 0; i < total.size(); i++) { copyList.add(total.get(i)); } return copyList; } }
- 组合总和 II - 这一题是元素不能完全相同
给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意：解集不能包含重复的组合。
来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/combination-sum-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40class Solution { List<List<Integer>> ans = new ArrayList<>(); boolean[] visit; public List<List<Integer>> combinationSum2(int[] candidates, int target) { Arrays.sort(candidates); visit = new boolean[candidates.length]; dfs(new ArrayList<>(), candidates, 0, 0, target); return ans; } void dfs(List<Integer> cur, int[] nums, int start, int curNum, int target) { if(curNum == target) { ans.add(copyList(cur)); } if(start == nums.length) { return; } // 和47不同的是47是取全排列，而本地元素相同也算重复，所有从start开始往后取，也就是说只能取后面的，不能取前面的，因为nums已经排序过了，这就避免了不同元素的乱序导致的重复。 仅仅只需改一下起点，就能得到和40题不同的去重效果 for(int i = start; i < nums.length; i++) { if(visit[i] || (i>0 && nums[i] == nums[i-1] && !visit[i-1])) continue; int temp = curNum+nums[i]; if(temp > target) break; cur.add(nums[i]); visit[i] = true; dfs(cur, nums, i+1, temp, target); cur.remove(cur.size()-1); visit[i] = false; } } List<Integer> copyList(List<Integer> total) { List<Integer> copyList = new ArrayList<>(); for(int i = 0; i < total.size(); i++) { copyList.add(total.get(i)); } return copyList; } }
快速选择 - 求第K大(小)元素或前K大(小)元素
求第K大(小)元素或前K大(小)元素如果不要求结果有序，完全没有必要将结果做完全排序。利用快速排序的思路，将集合分为大于指定值或者小于指定值的两个集合，再从目标集合里面继续找，放弃另外的集合，这样无需完全排序就能找到目标元素。
215 . 数组中的第K个最大元素 给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。 请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/kth-largest-element-in-an-array
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33class Solution { Random random = new Random(); public int findKthLargest(int[] nums, int k) { return findKthLargest(nums, 0, nums.length-1, k); } public int findKthLargest(int[] nums, int start, int end, int k) { int r = start + random.nextInt(end-start+1); sweep(nums, r, end); int j = start; for(int i = start; i < end; i++) { if(nums[i] > nums[end]) { sweep(nums, i, j); j++; } } sweep(nums, j, end); int leftLength = j - start; if(leftLength+1 == k) return nums[j]; if(k <= leftLength) { return findKthLargest(nums, start, j-1, k); // 则一部j-1和下面的j+1比较重要，因为如果不进行+1的话，对于元素相同的区间会出现一直无法剔除元素导致死循环的风险 } else { return findKthLargest(nums, j+1, end, k-leftLength-1); } } public void sweep(int[] nums, int i, int j) { int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; } }
二分查找
二分查找用来查找一个有序列表内与目标元素相等或者第一个大（小于）目标元素的位置。思路上和快速选择类型，不过快速选择是从无序的列表中选前K个元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19// 求比x大的第一个元素所在的位置 int searchIndex(int x){ if(0 == numList.size()) return 0; // 空就直接结束-如果是求相等，这里不能反悔0哦，可以反悔-1标识未找到 int start = 0; int end = numList.size()-1; // start是小于等于，而不是等于，因为收缩到最后一个元素，不是直接就认定结果了，最后一个也要判断 while(start<=end) { int mid = (end-start)/2 + start; if(numList.get(mid) <= x) { // 如果小于的话，那么说明在右边，start为mid+1，没什么说的 start = mid + 1; } else { // 如果大于的话就是mid-1，为什么放心-1呢，难道不怕这个mid刚好就是第一个大于目标元素的位置，这里剔除不会出错吗？ //其实是不会的，因为如果这样，那么最后肯定会收缩到mid-1处，此时start=end，然后判定mid<x，所以会+1，就回到这个位置了 end = mid-1; } } return start; }
最小(大)堆，求有序的前K个元素
如果要求求出前K个元素，且这K个元素有序，那么可以维护一个长度为K的最小（大）堆，而无需维护所有的元素顺序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution { public int[] kClosest(int[] points, int k) { // PriorityQueue默认是一个最小堆 PriorityQueue<Integer> pq = new PriorityQueue<Integer>(new Comparator<int[]>() { public int compare(Integer v1, Integer v2) { return v2 - v1; // 默认是v1-v2,即为最小堆， v2-v1就变成了最大堆，我的记忆方法就是默认最小堆，是按顺序的1-2 ，如果是2-1就是最大堆 } }); for (int i = 0; i < k; ++i) { pq.offer(points[i]); } int n = points.length; for (int i = k; i < n; ++i) { int dist = points[i]; if (dist < pq.peek()) { pq.poll(); pq.offer(dist); } } int[] ans = new int[k]; for (int i = 0; i < k; ++i) { ans[i] = pq.poll(); } return ans; } }
单调栈-划分区间求极致值
单调栈常用来在一个数组划出一个区间，这个区间具有某种运算条件，求拥有极致结果的区间或者直接求极致值。这种问题都可以转换为求数组中每个元素左边和右边第一个比他小（大）的，如果仅求单个元素，通过遍历就能实现，但是如果需要求多个元素的，每个元素都遍历就变的复杂了，此时就可以应用单吊栈了，单调栈内部维护一个单调递增(减)的元素下标。
也可以用来求最小序的去重结果，比如一个字符串串，求去除重复字符后的最小字典序，其实就是求一个最小单调栈的过程。
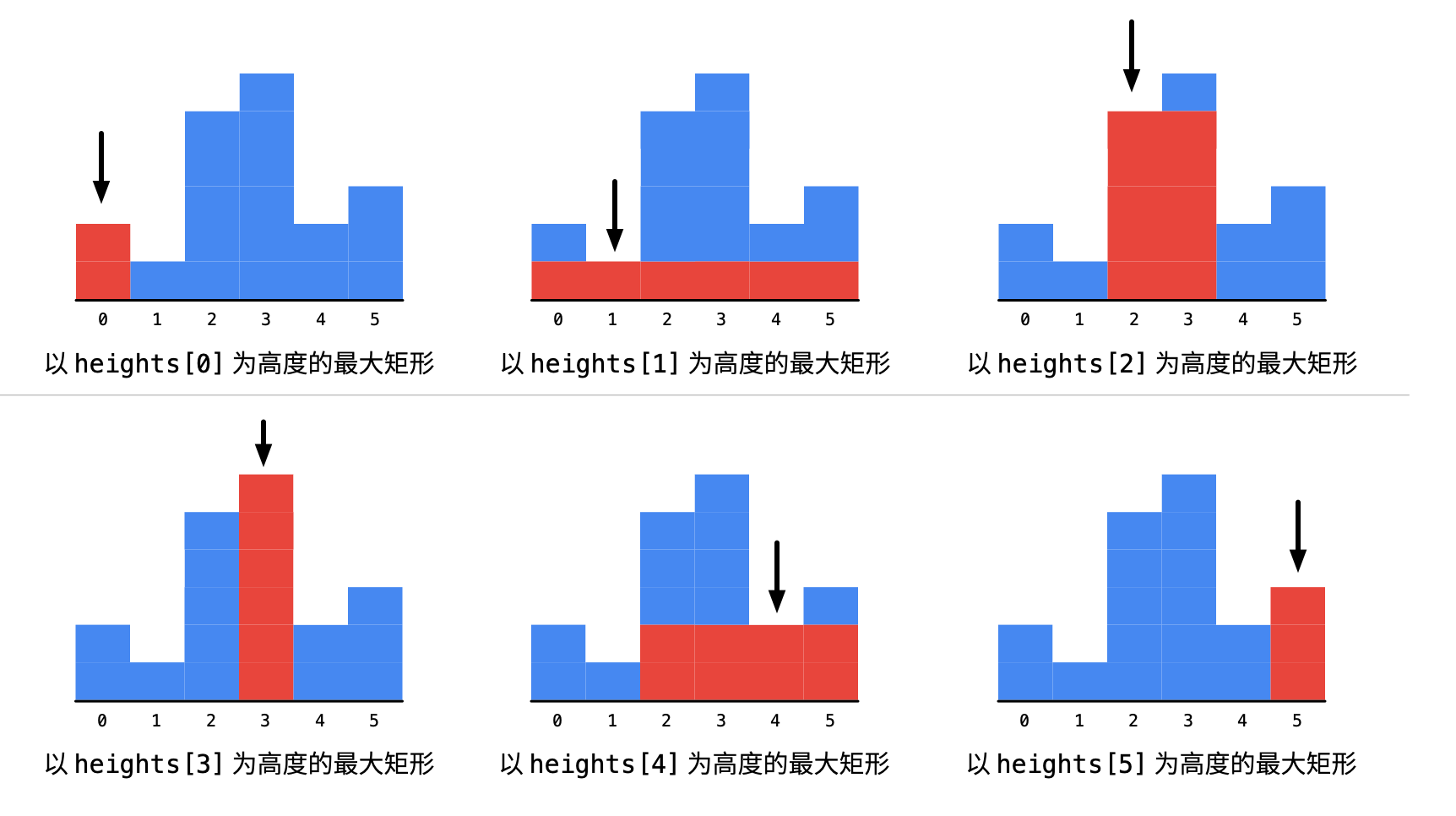
84 . 柱状图中最大的矩形 给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。 求在该柱状图中，能够勾勒出来的矩形的最大面积。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/kth-largest-element-in-an-array
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
这道题究根结底就是求每个元素左边和右边第一个比自己小的元素所在位置，结合下面这个图片更容易理解，图片来源于该题来自liweiwei1419分享的题解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution { public int largestRectangleArea(int[] heights) { int maxM = 0; Deque<Integer> stack = new ArrayDeque<>(); for(int i = 0; i < heights.length;i++) { while(!stack.isEmpty() && heights[stack.peek()] > heights[i]) { int j = stack.poll(); // i比poll出来的元素大，那么说明i就是j右边第一个比他小的元素，左边的话如果stack不为空，那么就是下一个peek出的元素，因为这是一个递增单调栈，如果为空，说明是左边界-1，注意是比他小的元素下标，如果为空说明0都比他大，那么0左边就是-1， 此时左右两个下标相减再+1就是长度 maxM = Math.max((i - (stack.isEmpty() ? -1 : stack.peek()) - 1)*heights[j], maxM); } stack.push(i); } // 如果栈内还有元素，说明是一个完整的单独递增栈，那么栈内的元素右边界是heights.length，和-1是同理的 while(!stack.isEmpty()) { int j = stack.poll(); maxM = Math.max((heights.length - (stack.isEmpty() ? -1 : stack.peek()) - 1)*heights[j], maxM); } return maxM; } }
出度（两端烧绳子求中点，无向图求中点）
无向图求最短路径，可以用出度的方式。具体方式为遍历关联关系，得出每个节点的度数表和相临节点关系，然后把度数最低的节点出度，并将其相邻节点的度数减-1，最后留下的就是到各个节点路径最短的节点。
310 . 最小高度树 树是一个无向图，其中任何两个顶点只通过一条路径连接。 换句话说，一个任何没有简单环路的连通图都是一棵树。给你一棵包含 n 个节点的树，标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges列表（每一个边都是一对标签），其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。
可选择树中任何一个节点作为根。当选择节点 x 作为根节点时，设结果树的高度为 h。在所有可能的树中，具有最小高度的树（即，min(h)）被称为 最小高度树 。
请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。
树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-height-trees/
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43class Solution { public List<Integer> findMinHeightTrees(int n, int[][] edges) { List<Integer> ans = null; if(n==1) { ans = new ArrayList(); ans.add(0); return ans; } int[] cs = new int[n]; // 度数 Map<Integer, List<Integer>> rel = new HashMap(); // 关联关系 int i; for(i = 0; i< n; i++) { rel.put(i, new ArrayList<Integer>()); } for(i = 0; i< edges.length; i++) { cs[edges[i][0]]++; cs[edges[i][1]]++; rel.get(edges[i][0]).add(edges[i][1]); rel.get(edges[i][1]).add(edges[i][0]); } ArrayDeque<Integer> ad = new ArrayDeque<Integer>(); for(i = 0; i< n; i++) { // 因为是树，所以最小度数肯定是1 if(cs[i] == 1) ad.offer(i); } while(!ad.isEmpty()) { ArrayDeque<Integer> adTemp = new ArrayDeque<Integer>(); ans = new ArrayList(); while(!ad.isEmpty()) { Integer num = ad.poll(); ans.add(num); for(int relNum : rel.get(num)) { cs[relNum]--; // 出度 if(cs[relNum] == 1) { adTemp.offer(relNum); } } } ad = adTemp; } return ans; }
多源广度(深度)优先搜索
正常的广度（深度）优先搜索，只有一个根节点，多源的则为多个根节点，由多个根节点的搜索共同决定结果。更简单的理解是：从树的某一层开始搜索，仅仅搜索大于该层的节点。理解这个，如何实现多源搜索就简单的多了。
常用于解决检索范围一个节点集合，或者后续的动作需要根据前面一层的动作决定的场景。
1765 . 地图中的最高点 给你一个大小为 m x n 的整数矩阵 isWater ，它代表了一个由 陆地 和 水域 单元格组成的地图。
如果 isWater[i][j] == 0 ，格子 (i, j) 是一个 陆地 格子。
如果 isWater[i][j] == 1 ，格子(i, j) 是一个 水域 格子。
你需要按照如下规则给每个单元格安排高度：
每个格子的高度都必须是非负的。 如果一个格子是是 水域 ，那么它的高度必须为 0 。 任意相邻的格子高度差 至多 为 1 。当两个格子在正东、南、西、北方向上相互紧挨着，就称它们为相邻的格子。（也就是说它们有一条公共边）
找到一种安排高度的方案，使得矩阵中的最高高度值 最大 。请你返回一个大小为 m x n 的整数矩阵 height ，其中 height[i][j] 是格子 (i, j)的高度。如果有多种解法，请返回 任意一个 。
这个就是典型的多源BFS，初始源为那些标记为水域的节点集合，把他周围没标记的标为1，然后再BFS为1的集合，标记周围为2，进行BFS操作，一直到遍历完成，即可得到结果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37class Solution { int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; public int[][] highestPeak(int[][] isWater) { int m = isWater.length, n = isWater[0].length; int[][] ans = new int[m][n]; for (int i = 0; i < m; ++i) { Arrays.fill(ans[i], -1); // -1 表示该格子尚未被访问过 } Queue<int[]> queue = new ArrayDeque<int[]>(); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (isWater[i][j] == 1) { ans[i][j] = 0; queue.offer(new int[]{i, j}); // 将所有水域入队 } } } while (!queue.isEmpty()) { int[] p = queue.poll(); for (int[] dir : dirs) { int x = p[0] + dir[0], y = p[1] + dir[1]; if (0 <= x && x < m && 0 <= y && y < n && ans[x][y] == -1) { ans[x][y] = ans[p[0]][p[1]] + 1; queue.offer(new int[]{x, y}); } } } return ans; } } 作者：LeetCode-Solution 链接：https://leetcode-cn.com/problems/map-of-highest-peak/solution/di-tu-zhong-de-zui-gao-dian-by-leetcode-jdkzr/ 来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
求一个集合(数组) 符合某种条件的(真)子集
此种场景可以用回溯法，递归数组，分别计算选和不选当前元素的场景。当选中时进行条件计算（因为选中时才会出现子集变动）。
- 统计按位或能得到最大值的子集数目
给你一个整数数组 nums ，请你找出 nums 子集 按位或 可能得到的 最大值 ，并返回按位或能得到最大值的 不同非空子集的数目 。
如果数组 a 可以由数组 b 删除一些元素（或不删除）得到，则认为数组 a 是数组 b 的一个 子集 。如果选中的元素下标位置不一样，则认为两个子集 不同 。
对数组 a 执行 按位或 ，结果等于 a[0] OR a[1] OR … OR a[a.length - 1]（下标从 0 开始）。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/count-number-of-maximum-bitwise-or-subsets
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution { int ans = 0; int maxSub; public int countMaxOrSubsets(int[] nums) { nextNum(0, 0, nums); return ans; } void nextNum(int curSub, int i, int[] nums) { if(i == nums.length) return; // 不选中 nextNum(curSub, i+1, nums); curSub |= nums[i]; // 选中后进行条件维护 if(curSub == maxSub) ans++; else if (curSub > maxSub) { ans = 1; maxSub = curSub; } // 选中递归 nextNum(curSub, i+1, nums); } }
最后
以上就是机智蓝天最近收集整理的关于助你刷题LeetCode - 常见算法（持续更新中）动态规划-后一个状态能由前一个状态转换来分治回溯并查集 - 算是否关联前序遍历（先序遍历）中序遍历双指针（快慢指针）从集合中选择满足条件的结果(去重或不去重)快速选择 - 求第K大(小)元素或前K大(小)元素二分查找最小(大)堆，求有序的前K个元素单调栈-划分区间求极致值出度（两端烧绳子求中点，无向图求中点）多源广度(深度)优先搜索求一个集合(数组) 符合某种条件的(真)子集的全部内容，更多相关助你刷题LeetCode内容请搜索靠谱客的其他文章。
发表评论 取消回复