leetcode算法集锦

本文是收集了LeetCode各路大神的思路，供自己和各位算友共同学习进不！！！
本文是收集了LeetCode各路大神的思路，供自己和各位算友共同学习进不！！！
本文是收集了LeetCode各路大神的思路，供自己和各位算友共同学习进不！！！

LCP 18. 早餐组合

小扣在秋日市集选择了一家早餐摊位，一维整型数组 staple 中记录了每种主食的价格，一维整型数组 drinks 中记录了每种饮料的价格。小扣的计划选择一份主食和一款饮料，且花费不超过 x 元。请返回小扣共有多少种购买方案。

注意：答案需要以 1e9 + 7 (1000000007) 为底取模，如：计算初始结果为：1000000008，请返回 1

示例 1：
输入：staple = [10,20,5], drinks = [5,5,2], x = 15
输出：6
解释：小扣有 6 种购买方案，所选主食与所选饮料在数组中对应的下标分别是：
第 1 种方案：staple[0] + drinks[0] = 10 + 5 = 15；
第 2 种方案：staple[0] + drinks[1] = 10 + 5 = 15；
第 3 种方案：staple[0] + drinks[2] = 10 + 2 = 12；
第 4 种方案：staple[2] + drinks[0] = 5 + 5 = 10；
第 5 种方案：staple[2] + drinks[1] = 5 + 5 = 10；
第 6 种方案：staple[2] + drinks[2] = 5 + 2 = 7。

示例 2：
输入：staple = [2,1,1], drinks = [8,9,5,1], x = 9
输出：8
解释：小扣有 8 种购买方案，所选主食与所选饮料在数组中对应的下标分别是：
第 1 种方案：staple[0] + drinks[2] = 2 + 5 = 7；
第 2 种方案：staple[0] + drinks[3] = 2 + 1 = 3；
第 3 种方案：staple[1] + drinks[0] = 1 + 8 = 9；
第 4 种方案：staple[1] + drinks[2] = 1 + 5 = 6；
第 5 种方案：staple[1] + drinks[3] = 1 + 1 = 2；
第 6 种方案：staple[2] + drinks[0] = 1 + 8 = 9；
第 7 种方案：staple[2] + drinks[2] = 1 + 5 = 6；
第 8 种方案：staple[2] + drinks[3] = 1 + 1 = 2；

提示：
1 <= staple.length <= 10^5
1 <= drinks.length <= 10^5
1 <= staple[i],drinks[i] <= 10^5
1 <= x <= 2*10^5

思路

1、排序
2、双指针
3、i 从前往后， j 从后往前，找到 staple[i] + drinks[j] <= x 的位置
4、就可以往答案里加了

class Solution {
public:
    int breakfastNumber(vector<int>& staple, vector<int>& drinks, int x) {
        const int mod = 1e9 + 7;
        int ans = 0;
        sort(staple.begin(), staple.end());
        sort(drinks.begin(), drinks.end());
        int j = drinks.size() - 1;
        for (int i = 0; i < staple.size(); i++) {
        	// i 从前往后， j 从后往前，找到 staple[i] + drinks[j] <= x 的位置
            while (j >= 0 && staple[i] + drinks[j] > x) j--;
            if (j == -1) break;
            ans += j + 1;
            ans %= mod;
        }
        return ans;
    }
};

LCP 19. 秋叶收藏集

小扣出去秋游，途中收集了一些红叶和黄叶，他利用这些叶子初步整理了一份秋叶收藏集 leaves， 字符串 leaves 仅包含小写字符 r 和 y， 其中字符 r 表示一片红叶，字符 y 表示一片黄叶。
出于美观整齐的考虑，小扣想要将收藏集中树叶的排列调整成「红、黄、红」三部分。每部分树叶数量可以不相等，但均需大于等于 1。每次调整操作，小扣可以将一片红叶替换成黄叶或者将一片黄叶替换成红叶。请问小扣最少需要多少次调整操作才能将秋叶收藏集调整完毕。

示例 1：
输入：leaves = “rrryyyrryyyrr”
输出：2
解释：调整两次，将中间的两片红叶替换成黄叶，得到 “rrryyyyyyyyrr”

示例 2：
输入：leaves = “ryr”
输出：0
解释：已符合要求，不需要额外操作

提示：
3 <= leaves.length <= 10^5
leaves 中只包含字符 ‘r’ 和字符 ‘y’

方法一：动态规划

思路与算法

由于我们想要将收藏集中树叶的排列调整成「红、黄、红」三部分，因此我们可以用 3 个状态分别表示其中的每一部分，即状态 0 和状态 2 分别表示前面和后面的红色部分，状态 1 表示黄色部分。

此时，我们就可以尝试使用动态规划解决本题了。我们用f[i][j] 表示对于第 0 片到第 i 片叶子（记为leaves[0…i]）进行调整操作，并且第 i 片叶子处于状态 j 时的最小操作次数。在推导状态转移方程时，我们可以分别对于每一种状态进行分析。

当 j=0 时，我们需要将第 i 片叶子变成红色，并且第 i−1 片叶子也只能处于 j=0 的状态（因为没有编号更小的状态了），因此有状态转移方程：
f[i][0]=f[i−1][0]+isYellow(i)

其中 isYellow(i) 为示性函数，当第 i 片叶子为黄色时为 1，红色时为 0。

当 j=1 时，我们需要将第 i片叶子变成黄色，而第 i−1 片叶子既可以处于 j=1 的状态，也可以处于 j=0 的状态，我们选择其中的较小值，因此有状态转移方程：

f[i][1]=min{f[i−1][0],f[i−1][1]}+isRed(i)

其中 isRed(i) 为示性函数，当第 i片叶子为红色时为 1，黄色时为 0。

当 j=2 时，我们需要将第 i 片叶子变成红色，而第 i−1 片叶子即可以处于 j=2 的状态，也可以处于 j=1 的状态（注意这里不能处于 j=0 的状态，因为每一种状态包含的叶子数量必须至少为 1），我们选择其中的较小值，因此有状态转移方程：

f[i][2]=min{f[i−1][1],f[i−1][2]}+isYellow(i)

最终的答案即为 f[n−1][2]，其中 nn 是字符串leaves 的长度，也就是树叶的总数。

细节

由于 因为每一种状态包含的叶子数量必须至少为 1，因此不仅需要特别注意 j=2 时的状态转移方程，还需要考虑每个状态本身是否是符合要求的。对于状态 f[i][j] 而言，它包含了leaves[0…i] 共 i+1 片叶子以及 j+1个状态，因此 叶子的数量必须大于等于状态的数量，即满足i≥j。这样一来，所有 i<j 的状态 f[i][j] 都是不符合要求的。观察上面的状态转移方程，我们在每一步转移时都是取最小值，因此我们可以将所有不符合要求的状态置为一个极大值（例如n+1 或整数类型的上限等）。

同时需要注意的是，当 i=0 时，f[i][…] 会从f[i−1][…] 转移而来，但后者是没有意义的，因此我们需要对 f[i][…] 进行特殊处理。由于当 i=0 时，j 也只能为 0，因此我们有：
f[0][0]=isYellow(0)
作为唯一的边界条件。

class Solution {
    public int minimumOperations(String leaves) {
        int n = leaves.length();
        int[][] f = new int[n][3];
        f[0][0] = leaves.charAt(0) == 'y' ? 1 : 0;
        f[0][1] = f[0][2] = f[1][2] = Integer.MAX_VALUE;
        for (int i = 1; i < n; ++i) {
            int isRed = leaves.charAt(i) == 'r' ? 1 : 0;
            int isYellow = leaves.charAt(i) == 'y' ? 1 : 0;
            f[i][0] = f[i - 1][0] + isYellow;
            f[i][1] = Math.min(f[i - 1][0], f[i - 1][1]) + isRed;
            if (i >= 2) {
                f[i][2] = Math.min(f[i - 1][1], f[i - 1][2]) + isYellow;
            }
        }
        return f[n - 1][2];
    }
}

复杂度分析

时间复杂度：O(n)O(n)，其中 nn 是字符串 textit{leaves}leaves 的长度。
空间复杂度：O(n)O(n)。
可以使用「降维」优化，用三个变量代替状态数组，即可将空间复杂度降低到 O(1)O(1)。具体操作留给读者自行实现。

LCP 22. 黑白方格画

小扣注意到秋日市集上有一个创作黑白方格画的摊位。摊主给每个顾客提供一个固定在墙上的白色画板，画板不能转动。画板上有 n * n 的网格。绘画规则为，小扣可以选择任意多行以及任意多列的格子涂成黑色，所选行数、列数均可为 0。

小扣希望最终的成品上需要有 k 个黑色格子，请返回小扣共有多少种涂色方案。

注意：两个方案中任意一个相同位置的格子颜色不同，就视为不同的方案。

示例 1：
输入：n = 2, k = 2
输出：4
解释：一共有四种不同的方案：
第一种方案：涂第一列；
第二种方案：涂第二列；
第三种方案：涂第一行；
第四种方案：涂第二行。

示例 2：
输入：n = 2, k = 1
输出：0
解释：不可行，因为第一次涂色至少会涂两个黑格。

示例 3：
输入：n = 2, k = 4
输出：1
解释：共有 2*2=4 个格子，仅有一种涂色方案。

限制：
1 <= n <= 6
0 <= k <= n * n

简单的Java排列组合解法（超暴力）

首先我们依次枚举涂抹 N 行 M列的情况

每涂抹一行就相当于涂抹了 N * n个格子
每涂抹一列就相当于涂抹了 M * n个格子
而当我们选择涂抹 N 行 M 列时，重复涂过 N*M 个格子去掉这个重复数，再来判断是不是等于k
即
判断 ： （N * n + M * N）— N * M == k
当我们得出某个 N 和 M 组合能够得到k，我们就需要通过数学计算排列组合总数。

class Solution {
    public int paintingPlan(int n, int k) {
        int res = 0;
        //边界问题
        if(k == 0)return 1;
        if(k == n * n)return 1;

        //第一层循环表示涂 i 行 第二层循环表示涂 j 列
        for(int i = 0;i <= n;i++){
            for(int j = 0;j <= n;j++)
                //当你涂了 i 行 j 列  则有 i * n + j * n个方格被涂过了
                //去掉重复计入的 i*j个方格 是否等于结果k
                if((i*n) + (j*n) - (i*j) == k) {
                    res += C(i,n) * C(j,n);
                }
        }
        return res;
    }

    //数学里的排列组合 C(愚蠢式写法，勿计较)
    public int C(int x,int y){
        if(x == 0)return 1;
        int n = 1;
        for(int i = 0;i < x;i++){
            n *= (y - i);
        }
        for(int i = 1;i <= x;i++){
            n /= i;
        }
        return n;
    }
}

440. 字典序的第K小数字

给定整数 n 和 k，找到 1 到 n 中字典序第 k 小的数字。

注意：1 ≤ k ≤ n ≤ 109。

示例 :
输入:
n: 13 k: 2
输出:
10

解释:
字典序的排列是 [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9]，所以第二小的数字是 10。

什么是字典序？

简而言之，就是根据数字的前缀进行排序，
比如 10 < 9，因为 10 的前缀是 1，比 9 小。
再比如 112 < 12，因为 112 的前缀 11 小于 12。

这样排序下来，会跟平常的升序排序会有非常大的不同。先给你一个直观的感受，一个数乘 10，或者加 1，哪个大？可能你会吃惊，后者会更大。
但其实掌握它的本质之后，你一点都不会吃惊。

问题建模：

画一个图你就懂了。

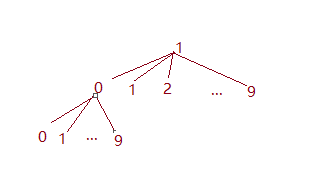
每一个节点都拥有 10 个孩子节点，因为作为一个前缀 ，它后面可以接 0~9 这十个数字。而且你可以非常容易地发现，整个字典序排列也就是对十叉树进行先序遍历。1, 10, 100, 101, … 11, 110 …

回到题目的意思，我们需要找到排在第k位的数。找到他的排位，需要搞清楚三件事情:

怎么确定一个前缀下所有子节点的个数？
如果第 k 个数在当前的前缀下，怎么继续往下面的子节点找？
如果第 k 个数不在当前的前缀，即当前的前缀比较小，如何扩大前缀，增大寻找的范围？
接下来 ，我们一一拆解这些问题。

理顺思路：

1. 确定指定前缀下所有子节点数

现在的任务就是给定一个前缀，返回下面子节点总数。
我们现在的思路就是用下一个前缀的起点减去当前前缀的起点，那么就是当前前缀下的所有子节点数总和啦。

//prefix是前缀，n是上界
var getCount = (prefix, n) => {
    let cur = prefix;
    let next = prefix + 1;//下一个前缀
    let count = 0;
    //当前的前缀当然不能大于上界
    while(cur <= n) {
        count += next - cur;//下一个前缀的起点减去当前前缀的起点
        cur *= 10; 
        next *= 10;
        // 如果说刚刚prefix是1，next是2，那么现在分别变成10和20
        // 1为前缀的子节点增加10个，十叉树增加一层, 变成了两层
        
        // 如果说现在prefix是10，next是20，那么现在分别变成100和200，
        // 1为前缀的子节点增加100个，十叉树又增加了一层，变成了三层
    }
    return count;//把当前前缀下的子节点和返回去。
}

当然，不知道大家发现一个问题没有，当 next 的值大于上界的时候，那以这个前缀为根节点的十叉树就不是满十叉树了啊，应该到上界那里，后面都不再有子节点。因此，count += next - curcount+=next−cur 还是有些问题的，我们来修正这个问题:

count += Math.min(n+1, next) - cur;

你可能会问:咦？怎么是 n+1 ,而不是 nn 呢？不是说好了 nn 是上界吗？

我举个例子，假若现在上界 nn为 12，算出以 1 为前缀的子节点数，首先 1 本身是一个节点，接下来要算下面 10，11，12，一共有 4 个子节点。

那么如果用 Math.min(n, next) - curMath.min(n,next)−cur 会怎么样？

这时候算出来会少一个，12 - 10 加上根节点，最后只有 3 个。因此我们务必要写 n+1。

现在，我们搞定了前缀的子节点数问题。

2. 第k个数在当前前缀下

现在无非就是往子树里面去看。
prefix这样处理就可以了。

prefix *= 10

3. 第k个数不在当前前缀下

说白了，当前的前缀小了嘛，我们扩大前缀。

prefix ++;

框架搭建：
整合一下刚刚的思路。

let findKthNumber = function(n, k) {
  let p = 1;//作为一个指针，指向当前所在位置，当p==k时，也就是到了排位第k的数
  let prefix = 1;//前缀
  while(p < k) {
    let count = getNumber(prefix, n);//获得当前前缀下所有子节点的和
    if(p + count > k) { //第k个数在当前前缀下
      prefix *= 10;
      p++; //把指针指向了第一个子节点的位置，比如11乘10后变成110，指针从11指向了110
    } else if(p + count <= k) { //第k个数不在当前前缀下
      prefix ++;
      p += count;//注意这里的操作，把指针指向了下一前缀的起点
    }
  }
  return prefix;
};

完整代码展示：

/**
 * @param {number} n
 * @param {number} k
 * @return {number}
 */
var findKthNumber = function(n, k) {
  let getCount = (prefix, n) => {
    let count =  0;
    for(let cur = prefix, next = prefix + 1; cur <= n; cur *= 10, next *= 10) 
      count += Math.min(next, n+1) - cur;
    return count;
  }
  let p = 1;
  let prefix = 1;
  while(p < k) {
    let count = getCount(prefix, n);
    if(p + count > k) {
      prefix *= 10;
      p++;
    } else if(p + count <= k) {
      prefix ++;
      p += count;
    }
  }
  return prefix;
};

最后

以上就是昏睡老师为你收集整理的leetcode算法集锦的全部内容，希望文章能够帮你解决leetcode算法集锦所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。