matlab画正态分布曲线_正态分布检验

1. 什么情况下需要做正态分布检验

2. 如何检验

   1. Shapiro-Wilk检验(W检验)

   2. Kolmogorov-Smirnov正态性检验(D检验)

   3. Q-Q图法

3. 频率分布直方图、概率密度图、理想正态分布的概率密度图

4. QQ图与直方图组合

1.什么情况下需要做正态分布检验

• 统计推断的前提假设是正态分布

• 模型基于正态分布

2.如何检验

参考：

https://bbs.pinggu.org/linkto.php?url=http%3A%2F%2Fblog.sina.com.cn%2Fs%2Fblog_65efeb0c0100htz7.html

介绍了三种正态性检验的方法：

1. 计算综合统计量 夏皮罗-威尔克Shapiro-Wilk法(W检验)，达戈斯提诺D′Agostino法

2. 正态分布的拟合优度检验 柯尔莫哥洛夫Kolmogorov-Smirov法检验

3. 图示法 分位数图(Quantile Quantile plot，简称QQ图)

1. Shapiro-Wilk检验(W检验)

基础函数 shapiro.test() fBasics包 normalTest()、shapiroTest()也是调用shapiro.test(x)

这些函数的结果一致，样本大小必需在3和5000之间

2. Kolmogorov-Smirnov正态性检验(D检验)

Kolmogorov - Smirnov是比较精确的正态检验法

nortest包 lillie.test(更精确) fBasics包 ksnormTest()、lillieTest(更精确)

SPSS 规定：当样本含量3 ≤ n ≤ 5000时，结果以Shapiro - Wilk(W检验)为准，当样本含量n > 5000结果以Kolmogorov - Smirnov为准。SAS 规定：当样本含量n ≤ 2000时，结果以Shapiro - Wilk(W检验)为准，当样本含量n > 2000时，结果以Kolmogorov - Smirnov为准。

参考 http://tiramisutes.github.io/2015/10/08/ANOVA.html https://www.cnblogs.com/blueicely/archive/2013/01/08/2850929.html

3. Q-Q图法

QQ图是怎么画的

详细原理：

http://www.docin.com/p-44022618.html https://znonymous.me/2016/06/23/q-q-plot-introduction/

回忆以前学习标准正态分布的时候，讲过累积分布函数和概率密度函数，其中将概率密度函数积分能得到累积分布函数。下面是分位数的定义：

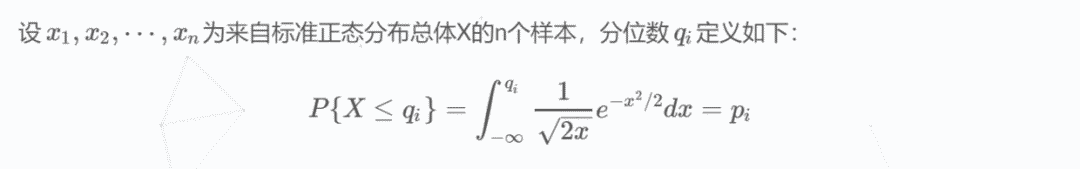
以前还做过这种题，给你一个比例p，让你求一个数，使得小于等于这个数的比例是p，或者反过来。按照这个定义，我觉得中位数可以叫做1/2分位数，表示小于等于这个数的数据量占总体数据量的1/2。所以分位数和比例p之间是存在对应关系的，这种关系在给定的数据集中是唯一的。

由统计学可以证明：若数据y1,y2,⋯,yn的分布与正态分布非常接近，则点 (qi,yi)(i=1,2,⋯,n)应大致成一条直线。

1. 将原始观察数据由小到大排列，依次表示p1,p2,⋯,pn分位数

2. 如果符合标准正态分布，对应于p1,p2,⋯,pn这些比例，其分位数应该是q1,q2,⋯,qn

3. 用数对 (qi,yi)(i=1,2,⋯,n)画散点图，并观察它们是否成直线

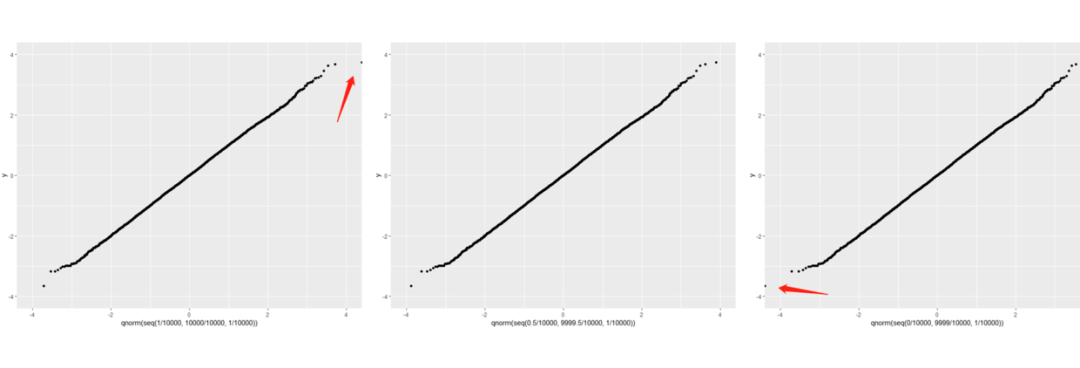
这里面需要我们求的只有第2步，根据pi求qi。按照前面的定义，这里pi应该等于i/n(i=1,2,...,n)。我在一些理论博客上面看到这里用的是(i-0.5)/n，为什么会这样？我的理解是：一方面当n比较大的时候其实p值基本没区别，另一方面我用本来就是正态分布的一些数据画了i，i-0.5，i-1三个图发现i-0.5是最直的，i/n的图右上角点向右偏移，(i-1)/n的图左下角的点向左偏移，这两种情况都出现了一个“无穷远”的点，相比之下(i-0.5)/n更符合通过笔直程度判断正态分布这个“主题”。

举个例子：

y rnorm(10000)

y sort(y)

# i - 1

ggplot(NULL,aes(qnorm(seq(0/10000,9999/10000,1/10000)),y))+

geom_point()+

xlim(-4,4)+ylim(-4,4)

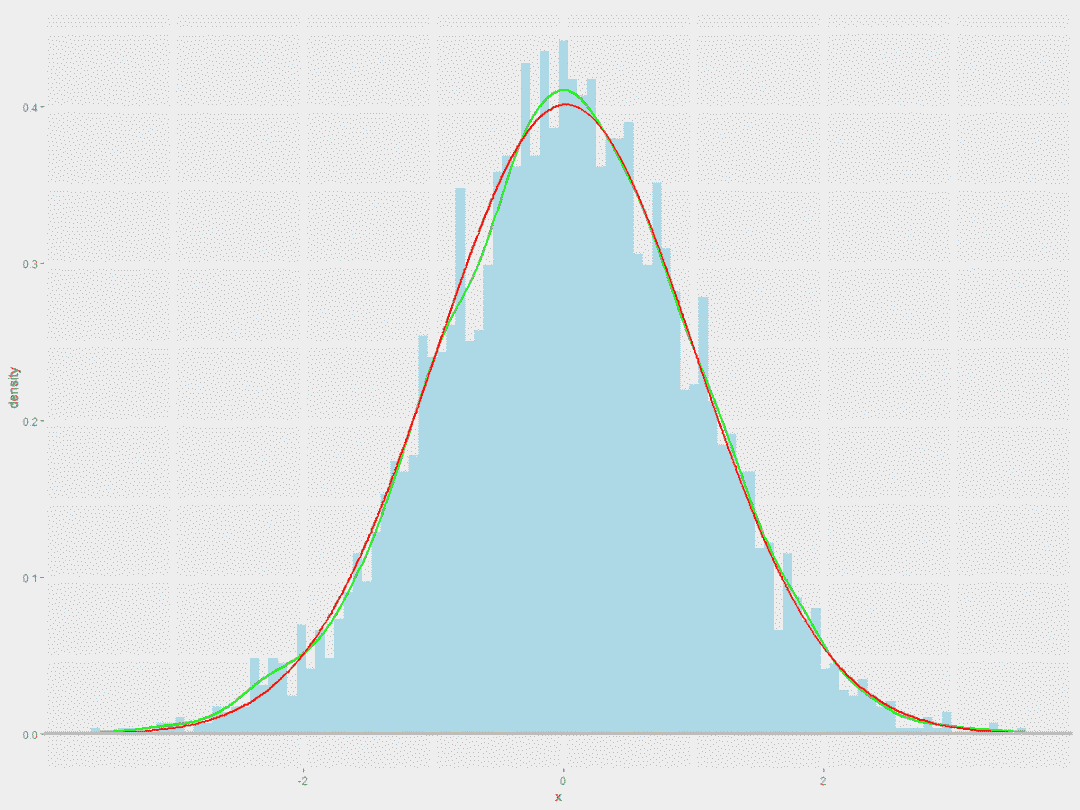
3.频率分布直方图、概率密度图、理想正态分布的概率密度图

只能辅助判断并不是一种正态分布检验方法

频数分布直方图来定性地判断数据分布正态性,决不是严格的正态性检验

set.seed(20190816)

x rnorm(4000)

expected_densitydnorm(x,mean(x),sd(x))

ggplot(NULL,aes(x=x,y=..density..))+geom_histogram(bins=100,fill="light blue")+

geom_density(color="green",size=1)+

geom_line(aes(x,expected_density),color="red",size=1)+

geom_hline(yintercept = 0,color="grey",size=1.5)

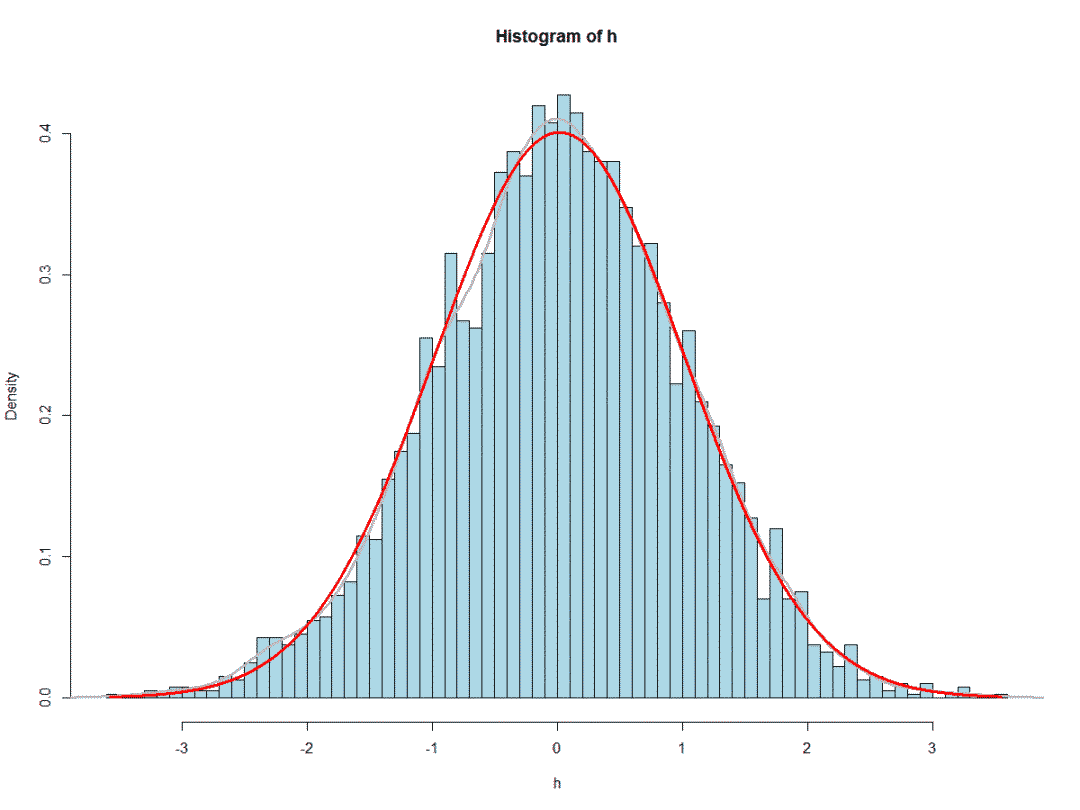
或者

set.seed(20190816)

hrnorm(4000)

#直方图

hist(h,freq = F,col = "light blue",breaks = 100)

#加密度曲线

lines(density(h), col="grey", lwd=3)

#加正态密度曲线

xfitseq(min(h),max(h),length=4000)

yfitdnorm(xfit,mean(h),sd(h))

lines(xfit,yfit,col="red",lwd=3)

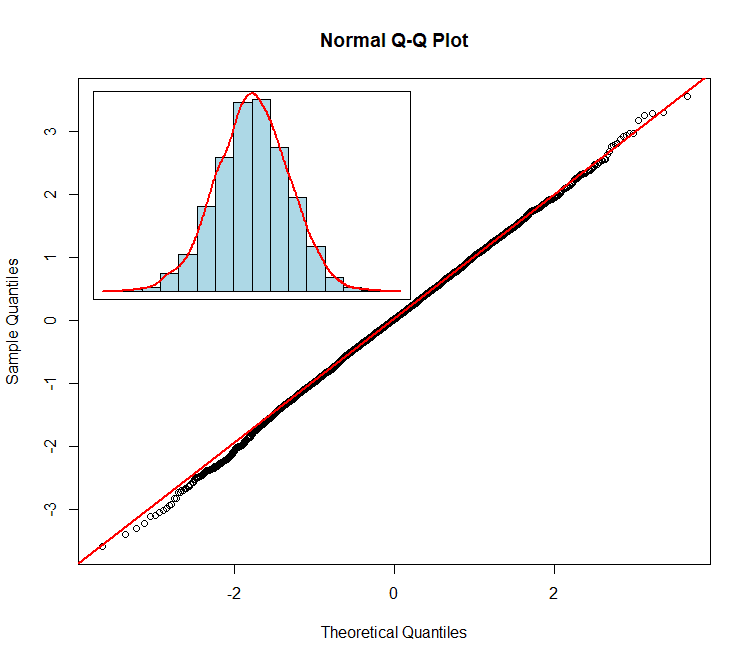
4.QQ图与直方图组合

参考：

http://blog.sina.com.cn/s/blog_8d8d6cde01017d1b.html https://blog.csdn.net/XIUXIU179/article/details/80107269

set.seed(20190816)

hrnorm(4000)

qqnorm(h)

qqline(h, col="red",lwd=2)

op par(fig=c(0.02,0.6,0.4,0.98), new=TRUE)

hist(h, probability=T, col="light blue", xlab="", ylab="", main="", axes=F)

lines(density(h), col="red", lwd=2)

box()

par(op)