生成服从正态分布的随机数

首先，谢谢szy-8910的博文 正态分布随机数的产生 

这里摘录部分：

二、任意分布随机数的产生

     下面提出了一种已知概率密度函数的分布的随机数的产生方法，以典型的正态分布为例来说名任意分布的随机数的产生方法。

     如果一个随机数序列服从一维正态分布，那么它有有如下的概率密度函数：

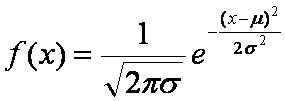（1-1）

其中μ，σ（ >0）为常数，它们分别为数学期望和均方差，如果读者对数学期望和均方差的概念还不大清楚，请查阅有关概率论的书。如果取μ =0，σ =0.2,则其曲线为

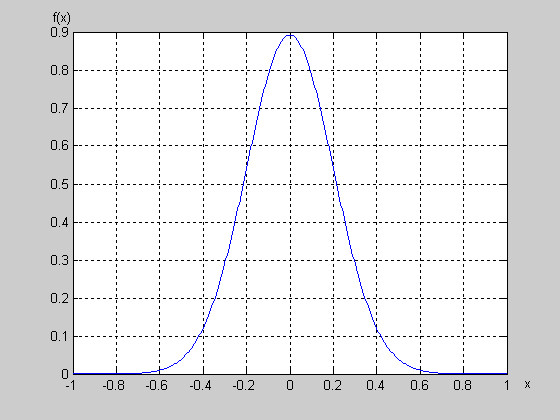
                             图2 正态分布的概率密度函数曲线

     从图中可以看出，在μ附近的概率密度大，远离μ的地方概率密度小，我们要产生的随机数要服从这种分布，就是要使产生的随机数在μ附近的概率要大，远离μ处小，怎样保证这一点呢，可以采用如下的方法：在图2的大矩形中随机产生点，这些点是平均分布的，如果产生的点落在概率密度曲线的下方，则认为产生的点是符合要求的，将它们保留，如果在概率密度曲线的上方，则认为这些点不合格，将它们去处。如果随机产生了一大批在整个矩形中均匀分布的点，那么被保留下来的点的横坐标就服从了正态分布。可以设想，由于在μ处的f(x)的值比较大，理所当然的在μ附近的点个数要多，远离μ处的少，这从面积上就可以看出来。我们要产生的随机数就是这里的横坐标。

     基于以上思想，我们可以用程序实现在一定范围内服从正态分布的随机数。程序如下：

参数说明：  double miu：μ，正态函数的数学期望

                    double sigma：σ，正态函数的均方差

                    double min,double max，表明产生的随机数的范围

============================================以下是我的程序部分========================================

//生成服从正态分布的随机数
 double NormalRandom(double miu,double sigma)//产生正态分布随机数
 {
	double x;
	double y;
	double dScope;
	double maxY = Normal(miu,miu,sigma);
	do
	{
		x = AverageRandom(-3*sigma,3*sigma);
		y = Normal(x, miu, sigma);
		dScope = AverageRandom(0, maxY);
	}while( dScope > y);
	return x;
 }

double Normal(double x,double miu,double sigma) //概率密度函数
{
	return 1.0/sqrt(2*PI*sigma) * exp(-1*(x-miu)*(x-miu)/(2*sigma*sigma));
}

int AverageRandom(int  min,int max)
{
	srand(time(0));
	return (double)(max-min) * rand()/RAND_MAX + min ;
}

最后

以上就是阳光水杯为你收集整理的生成服从正态分布的随机数的全部内容，希望文章能够帮你解决生成服从正态分布的随机数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。