Matlab入门-向量及多项式-一维行列向量创建的四种方法及 求根公式

数组（Array）：按行（row）和列（column）顺序排列的实数或复数的有序集称为数组。

数组的分类：
一维数组，也称行向量（row vector）和列向量（column vector）
多维数组即矩阵

创建一维数组行变量的方法：

1、使用 [ ]:

a=[1 2 3 4 5] 或 a=[1,2,3,4,5]

2、使用 “：” 操作符

如创建以1~10顺序排列的整数为元素的行向量b：

1
2
b=1:10

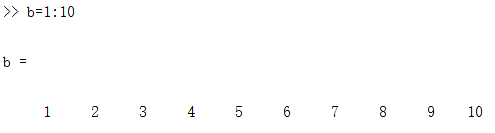
在这里1指的是从1开始，10指的是不能超过10.

也可以加入步长如：

1
2
c=1:2:8

从1开始，每次增加步长2，一直加到不超过8。如果不设置步长的话步长自动为1.

3、利用函数x=linspace( x1,x2,n)

说明：

该函数生成一个由n个元素组成的行向量
x1为第一个元素，x2为第二个元素，n为元素个数
也就是说均匀地生成 从x1到x2共n个元素的行向量

如：

1
2
3
在这里插入代码片
linspace(1, 2,5)

注：如果忽略n，系统默认生成100个元素

4、利用函数logspace(a,b,n)

与linspace()相似，logspace()生成的是从10的a次方开始，到10的b次方结束，共n个变量的一维数组。

创建一维数组列向量的方法：

创建一维度列向量与一维行向量的方法相同，都是四种，只需在行向量的基础上加个转置即可。

用’来表示转置

如：

1
2
a=[1 2 3]'

或：

1
2
a=[1,2,3]'

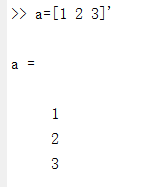
另也可用 ; 来表示列

1
2
a=[1;2;3]

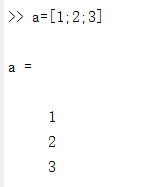
注：'表示的转制是共轭专制。也就是说实数的共轭转置可以将行向量变成列向量，这是因为在实数里，共轭转置和转置是没有区别的。如:

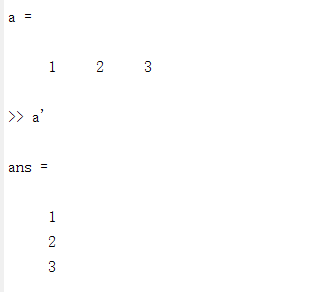
但是复数的转置不是这样，共轭转置会使其 行列变换，并且变成共轭：

那么在复数里的转置为.’

一维数组的应用：

求5x^5 - 3x^3 + 7x^2- 92x+13=0的全部根

1
2
3
p=[5,0,-3,7,-92,13]; %建立多项式系数向量
x=roots(p) %求根

最后

以上就是闪闪中心最近收集整理的关于Matlab入门-向量及多项式-一维行列向量创建的四种方法及 求根公式的全部内容，更多相关Matlab入门-向量及多项式-一维行列向量创建的四种方法及内容请搜索靠谱客的其他文章。