统计计算系列文章目录

第一话 统计计算之随机变量生成方法

提示：写完文章后，目录可以自动生成，如何生成可参考右边的帮助文档

1 引言

计算统计的基本工具就是要从指定的概率分布中生成随机变量，最基本最重要的是均匀分布的伪随机数生成器，其他概率分布的随机数生成方法大都依赖于均匀分布随机数生成器。
在R语言中，均匀分布的随机数的生成为：

runif(n) #generate a vector of size n in [0,1]
runif(n,a,b) #generate n Uniform(a, b) numbers
matrix(runif(n*m),n,m) #generate n by m matrix

另外，一个抽样函数sample()用于从一个有限总体中有放回或者无放回地抽样。

sample(0:1, size = 10, replace = TRUE) # replace = TRUE 表示有放回抽样
sample(1:100, size = 6, replace = FALSE) # replace = FALSE 表示有放回抽样
x=sample(1:3,size=100,replace=TRUE,prob=c(.2,.3,.5)) #sample from a multinomial dist.

2 随机数生成方法-逆变换方法(Inverse Transform Method)

逆变换方法主要使用以下定理：

• 定理1：如果X是一个连续的随机变量，其CDF(累积分布函数)为$F_X(x)$，则$U=F_X(X)\sim U(0,1)$。

关于定理1的证明，在此不再详细赘述，有兴趣可参见相关统计计算书籍。

根据定理1，得到一般连续型随机变量$X$的生成步骤：

• step1: 推导逆函数$F_X^{-1}(u)$；
• step2: 生成一个来自均匀分布$U(0,1)$的随机数$u$
• step3: 通过步骤1的逆函数产生$X$的随机数$x=F_X^{-1}(u)$

这个方法是生成随机数的最基本的方法，通常很容易应用在分布函数的逆$F_X^{-1}$很容易计算的前提下。

2.1 laplace分布随机数

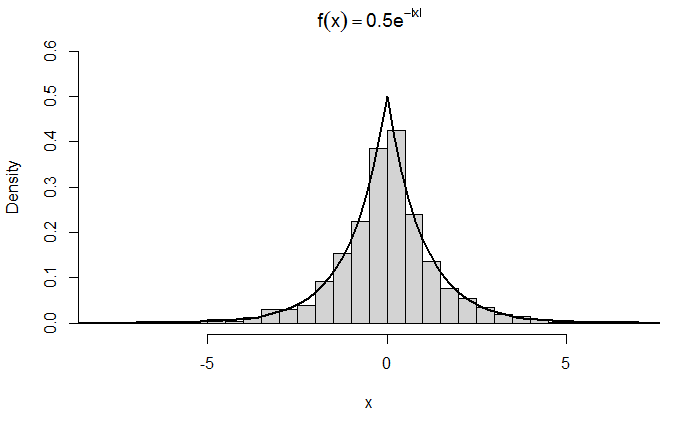
标准的Laplace分布的密度函数为$f(x)=\frac{1}{2}{e}^{-|x|},x\in \mathbb{R}$。使用逆变换方法从这个分布中生成样本量为1000的随机样本。并使用本章演示的方法来检查和比较生成的样本和目标分布。

根据标准的Laplace分布的密度函数通过求积分可以得知其分布函数为：

$$La(x;0,1)=\{\begin{array}{ll}\frac{1}{2}{e}^x,& x\le 0\\ 1-\frac{1}{2}{e}^{-x},& x>0\end{array}$$

根据以上分布函数，求逆函数如下：

$$F_X^{-1}=\{\begin{array}{ll}\log (2u)& 0<u\le \frac{1}{2}\\ \log \frac{1}{2(1-u)}& \frac{1}{2}<u<1\end{array}$$

根据以上逆函数，可以采用逆变换方法生成随机数,通过密度直方图对生成的随机数进行检验：：

set.seed(20201021)
u= runif(1000) # generate 1000 random numbers form U(0,1)
x <- ifelse(u<=0.5,log(2*u),log(1/(2*(1-u))))
mi =floor(min(x))
ma = ceiling(max(x))
hist(x,probability = TRUE,ylim = c(0,0.6),xlim = c(mi,ma),main = bquote(f(x)==0.5*e^{-abs(x)}),
     breaks = seq(mi,ma,by = 0.5))
data.frame(mean(x),sd(x))
y <- seq(-10,10,0.2)
lines(y,0.5*exp(-abs(y)),lwd = 2) #density curve f(x)

2.2 Pareto(a, b) 分布随机数

Pareto(a, b) 分布的cdf如下：
$$F(x)=1-{\left(\frac{b}{x}\right)}^a,x\ge b>0,a>0$$
推导概率逆变换函数$F^{-1}(U)$，并且使用逆变换方法来模拟生成Pareto(2, 2)的随机数。用Pareto(2，2)密度叠加的样本密度直方图进行比较。

通过计算Pareto(a, b) 分布F(X)的逆$F^{-1}(U)$得到：
$$F^{-1}(U)=\frac{b}{(1-u{)}^{1/a}}$$
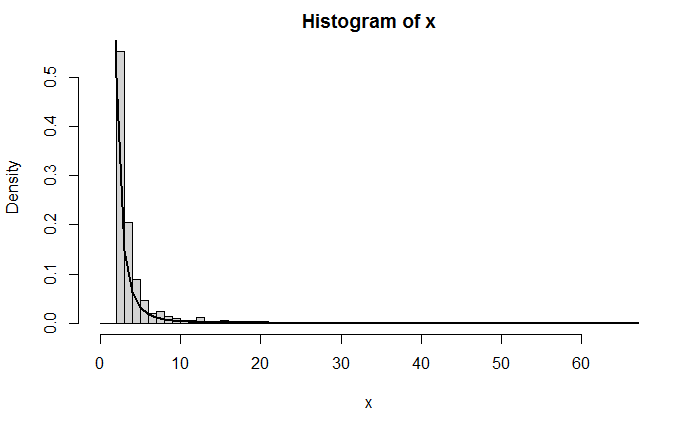
假设$a=2,b=2$,则产生Pareto随机数如下：

n = 1000;a = 2;b =2
set.seed(20201021)
u = runif(n)
x = b/(1-u)^(1/a) # the pareto random numbers
# hist(x,probability = TRUE,breaks = seq(0, ceiling(max(x)), 1))
ma = ceiling(max(x))
hist(x,probability = TRUE,breaks = seq(0,ma,1))
y = seq(0,ma,1)
lines(y,a*b/y^(a+1),lwd = 2)

3 转换方法

例：
由对数正态分布的性质可知，假设$X=e^Y,Y\sim N\left(\mu ,{\sigma }^2\right),\log X\sim N\left(\mu ,{\sigma }^2\right)$,因此要想产生对数正态分布的随机数，必须先产生正态分布随机数。在此假设$\mu =0,\sigma =1$.

rlognormal = function(n,mu,sd){
  y = rnorm(n,mean = mu,sd = sd)
  x = exp(y)
  return(x)
}
n = 1000
x = rlognormal(n,0,1)
ma = ceiling(max(x))
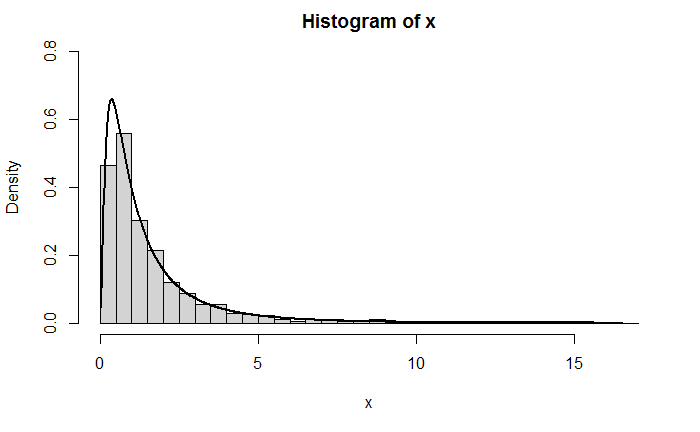
hist(x,probability = TRUE,xlim = c(0,ma),ylim = c(0,.8),breaks =  seq(0, ma,0.5))
# curve(dlnorm(x),add = TRUE,lwd = 2)
d = seq(from = min(x),to = max(x), length = n)
lines(d,dlnorm(d,meanlog = 0,sdlog = 1),lwd = 2)

4 混合方法

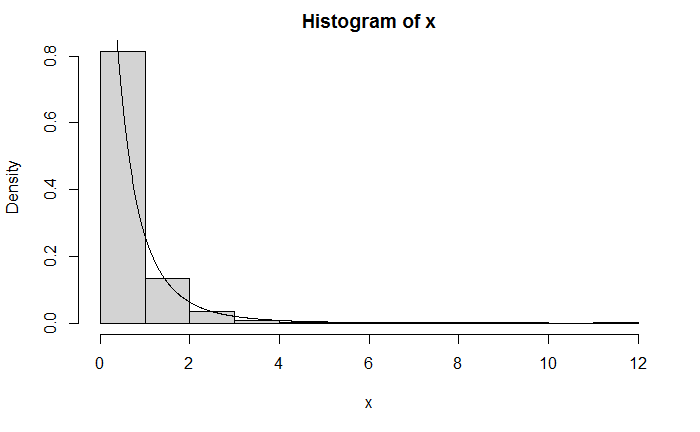
例：模拟连续的Exponential-Gamma mixture，假设比例参数$\Lambda$ 服从 $\mathrm{Gamma}(r,\beta )$分布，$Y$ 服从 $\mathrm{Exp}(\Lambda )$ 分布。$(Y\mid \Lambda =\lambda )\sim f_Y(y\mid \lambda )=\lambda e^{-\lambda y}$，给定$r=4,\beta =2$,从这个混合分布中产生1000个观测值。

set.seed(20201021)
r = 4; beta = 2
n = 1000
lambda = rgamma(n,r,beta)
x = rexp(n,lambda)
hist(x,probability = TRUE)
#check : Exponential-Gamma mixture is the Pareto distribution,so use the pdf of Pareto distribution
y = seq(min(x),max(x),length = n)
lines(y,64/(2+y)^5)
#library(actuar)
#lines(y,dpareto(y,shape = r,scale = 2))

5 生成wishart分布随机数

写一个基于Bartlett 分解的函数用于生成$W_d(\Sigma ,df)$(Wishart)分布的随机样本（$n>d+1>=1$）

r.Wishart = function(n,df,Sigma){
  # n : the sample size
  # df: the freedom of Wishart distribution
  #Sigma: the parameter of Wishart distribution
  d = nrow(Sigma)
  x = array(0,dim = c(d,d,n))
  for (i in 1:n) {
    T = x[,,i]
    Tij = rnorm(d*(d-1)/2,0,1)
    T[which(lower.tri(T))] = Tij # upper triangular elements in place of Tij
    len = 1:d
    df2 = df - len + 1
    Tii = sqrt(rchisq(d,df2))
    diag(T) = Tii # the elements of diagonal in place of Tii
    A = T %*% t(T)
    L = t(chol(Sigma)) # evaluate the lower triangular matrix
    x[,,i] = L %*% A %*% t(L)
  }
  return(x)
}

调用r.Wishart()函数的示例。

Sigma = matrix(c(5,1,1,3),2,2) # the covirance parameters for Wishart distribution
df = 50  # the freedom parameters for Wishart distribution
n = 1000 # sample size
set.seed(20201021)
x = r.Wishart(n,df,Sigma)

检查生成的Wishart分布的正确性主要采用Wishart分布的均值性质：$W\sim W_p(df,\Sigma ),则E(W)=df\ast \Sigma$

EWhat = apply(x,1:2,mean)  # Empirical result
EW = df*Sigma   # real result
list(EWhat = EWhat,EW = EW)

6 随机过程

计数过程记录在时间t之前发生的事件或到达的次数。下面介绍两个基本概念：独立增量和平稳增量

• 独立增量： 如果在不相交的时间间隔内到达的次数(或事件的次数)是独立的，则计数过程具有独立的增量。
• 平稳增量：如果间隔中发生的事件次数仅取决于间隔的长度，则计数过程具有平稳增量。

计数过程的一个例子是泊松过程。

为了通过模拟研究计数过程，我们可以生成一个在一定时间内记录事件的过程的实现(relization)。 连续到达的时间集记录了结果并确定任意时间$t$时的状态$X(t)$。 在模拟中，到达的时间的顺序必须是有限的。 模拟计数过程的一种方法是选择足够长的时间间隔，并在此间隔中生成到达时间或到达间隔时间。

齐次泊松过程（Poisson Processes）

速率为$\lambda$的齐次Poisson过程$N（t）,t\ge 0$是一个具有独立增量的计数过程，使得N（0）= 0且

到达时间T1，T2，…是连续到达之间的时间。到达的间隔时间是比率为λ的独立同分布的指数分布，其取自上式和指数分布的无记忆特性。

模拟一个泊松过程的一种方法是生成到达的间隔时间。 那么，第n次到达的时间为总和Sn = T1 + … + Tn（直到第n次到达的等待时间）。 到达的时间序列 { T n } n = 1 ∞ {T_n}_{n =1}^{∞} {Tn​}n=1∞​或到达时间序列 { S n } n = 1 ∞ {S_n}_{n =1}^{∞} {Sn​}n=1∞​是该过程的实现。 但是，实现是一个无限的序列，而不是单个数字。 在仿真中，到达时间 { T n } n = 1 N {T_n}_{n =1}^{N} {Tn​}n=1N​或到达时间 { S n } n = 1 N {S_n}_{n =1}^{N} {Sn​}n=1N​的有限序列是间隔$[0，S_N]$上该过程的仿真实现。

模拟Poisson过程的另一种方法是利用以下事实：给定N（t）= n，（无序）到达时间的条件分布与Uniform（0，t）中大小为n的随机样本的条件分布是一样的。

给定时间t的过程状态等价于在[0，t]区间上的到达次数，即min（k：Sk> t）-1。 即，N（t）＝ n-1，其中Sn是超过t的最小到达时间。

这个方法使用for 循环来执行算法生成到达的间隔时间，算法的速度较慢，可以采用向量化编程。

下面的代码阐述了一种简单的方法来模拟带有速率为$\lambda$的泊松过程。

假设我们需要得到$N(3)$,也就是在区间[0,3]上的到达次数。生成独立同分布的指数时间$T_i$（速率为$\lambda$）并且找到索引$n$，也即是累积求和$S_n=T_1+...+T_n$首次超过3。那么在[0,3]区间上到达的次数就是$n-1$，并且这个次数的平均值为$E[N(3)]=3\lambda$

lambda = 2 # the value of rate lambda
t0 = 3 # set the end time 
Tn = rexp(100,lambda) # generate the iid exponential Ti with rate lambda
Sn = cumsum(Tn) # arrival time
n = min(which(Sn>t0))
x = n -1 # the number of arrivals in [0,3]
round(Sn[1:n],4) #arrival time for per arrival

产生泊松过程的到达时间的另一种方法是基于以下事实：给定间隔（0，t）中的到达次数，无序的到达时间的条件分布是(0,t)上的均匀分布。假设给定(0,t)上的到达次数为n,到达时间$S_1,S_2,S_3,...,S_n$是联合分布作为一个样本量为n的有序的随机样本来自于uniform(0,t).

应用到达时间的条件分布，可以通过首先从Poisson（λt）分布生成随机观测值n，来模拟区间（0，t）上的Poisson（λ）过程，然后生成n个来自于均匀（0，t）的随机样本，并对随机样本进行排序以获得到达时间。

lambda= 2
t0 = 3
upper = 100
pp = numeric(10000){
	N = rpois(1, lambda * upper)
	Un = runif(N, 0, upper) # unordered arrival times
	Sn = sort(Un)    # arrival times
	n = min(which(Sn>t0)) # arrivals +1 in [0,t0]
	pp[i] = n-1   # arrivals in [0,t0]
}

pp = replicate(10000,expr = {
	N = rpois(1, lambda * upper)
	Un = runif(N, 0, upper) # unordered arrival times
	Sn = sort(Un)    # arrival times
	n = min(which(Sn>t0)) # arrivals +1 in [0,t0]
	n-1   # arrivals in [0,t0]
})

非齐次泊松过程（Poisson Processes）

更新过程（Renewal Processes）

最后

以上就是风中篮球为你收集整理的第一话 统计计算之随机变量生成方法统计计算系列文章目录1 引言2 随机数生成方法-逆变换方法(Inverse Transform Method)3 转换方法4 混合方法5 生成wishart分布随机数6 随机过程的全部内容，希望文章能够帮你解决第一话 统计计算之随机变量生成方法统计计算系列文章目录1 引言2 随机数生成方法-逆变换方法(Inverse Transform Method)3 转换方法4 混合方法5 生成wishart分布随机数6 随机过程所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。