通用的特殊矩阵

1. zeros函数：产生全0矩阵，即零矩阵。
2. ones函数：产生全1矩阵，即幺矩阵。
3. eye函数：产生对角线为1的矩阵。当矩阵是方阵时，得到一个单位矩阵。
4. rand函数：产生一个矩阵，矩阵元素在(0,1)上服从正态分布。
   fix(a + (b-a+1)*rand() )：产生一个矩阵，其中元素在[a,b]区间上均匀分布。
5. randn函数：产生一个矩阵，矩阵元素服从均值为0、方差为1的标准正太分布随机数。
   通过线性运算可以转换其均值和方差。

调用格式

>>zeros(m):产生m×m零矩阵。
>>zeros(m,n):产生m×n零矩阵。
>>zeros(size(A)):产生与A同样大小的零矩阵。

用于专门学科计算的特殊矩阵

1. 魔方矩阵—Magic Square：

• n阶魔方阵由1,2,3,4…,n²共n²个整数组成，且每行、每列以及主、副对角线上各n个元素之和都相等。
• n阶魔方矩阵每行每列元素的和为(1+2+3+…+n²)/n = (n+n³)/2.
• n>2时，有很多不同的魔方阵。但MATLAB函数magic(n)产生一个特定的魔方阵。

>> magic(8)//调用格式

2. 范德蒙矩阵

• 对于vector v = [v₁，v₂，…，v_n]，范德蒙德矩阵的形式为：
  
• 调用格式：MATLAB中，函数vander(V)生成·以向量V为基础的Vandermonde矩阵。常用用于在各种通信系统的纠错编码中，例如：常用的Reed-Solomon编码即以Vandermonde矩阵为基础。

>>A = vander(1:5);
>>B = vander([1,2,3,4]);
 //vander(1,3)这种调用格式错误是因为它的括号内并不是一个向量。

3. 希尔伯特矩阵

• n阶希尔伯特矩阵的一般形式为：
  
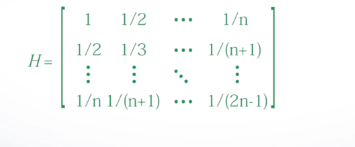
• 调用格式：

>>format rat;//设置输出格式为有理数输出
>>H = hilb(4);

4. 伴随矩阵

• 设多项式p(x)为a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀,，则多项式的伴随矩阵为：
  
  p(x)称为A的特征多项式，方程p(x)=0的根称为A的特征值。
• MATlLAB生成伴随矩阵的函数是compan( p )，其中p是一个多项式的系数向量，高次幂系数排在前，低次幂系数排在后。
  生成多项式x³-2x²-5x+6的伴随矩阵

>>p = [1,-2,-5,6];
>>A = compan(p);

5. 帕斯卡矩阵

最后

以上就是疯狂汉堡为你收集整理的Matlab-2.1特殊矩阵通用的特殊矩阵用于专门学科计算的特殊矩阵的全部内容，希望文章能够帮你解决Matlab-2.1特殊矩阵通用的特殊矩阵用于专门学科计算的特殊矩阵所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。