一、理论基础

1、Logistic映射

定义如下：$$x_{n+1}=\mu x_n(1-x_n),0<\mu \le 4,x_n\in (0,1)\text{\hspace{1em}(1)}$$其中，$x_n$是第$n$个混沌值，$n$表示迭代次数；$\mu$是混沌因子，$\mu \in (0,4]$。

2、Sine映射

Sine映射是单峰映射，其定义如下：$$x_{n+1}=\frac{\alpha }{4}\sin (\pi x_n),0<\alpha \le 4\text{\hspace{1em}(2)}$$其中，$\alpha$是混沌参数，$\alpha \in (0,4]$

3、Neuron映射

Neuron映射是具有非线性反馈的混沌映射。该映射利用双曲正切函数和指数函数构造混沌映射，其定义如下：$$x_{n+1}=\eta -2\tanh (\gamma )\exp (-3x_n^2)\text{\hspace{1em}(3)}$$其中，$\eta$表示衰减因子($0\le \eta \le 1$)；$\gamma$表示比例因子。

4、Tent映射

请参考这里。

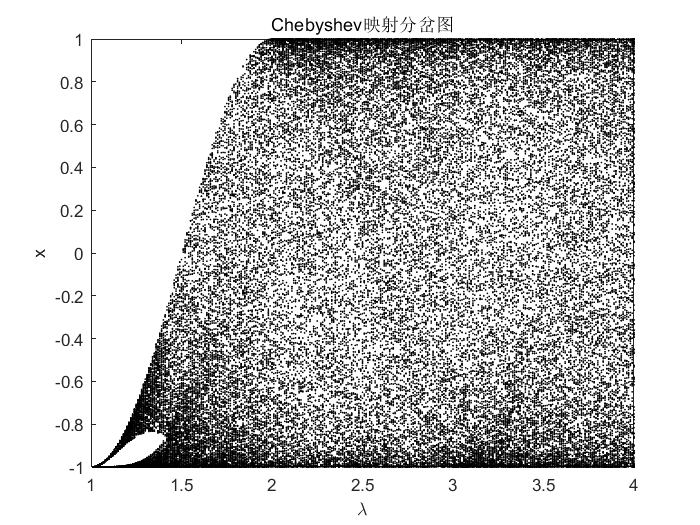
5、Chebyshev映射

Chebyshev映射是一种常见的对称区域映射。它通常用于神经网络、数字通信和安全问题。Chebyshev映射生成$(-1,1)$中的混沌序列。 其定义如下：$$x_{n+1}=\cos (\lambda \cdot {\cos }^{-1}{x}_n)\text{\hspace{1em}(4)}$$其中，$\lambda$表示混沌参数。

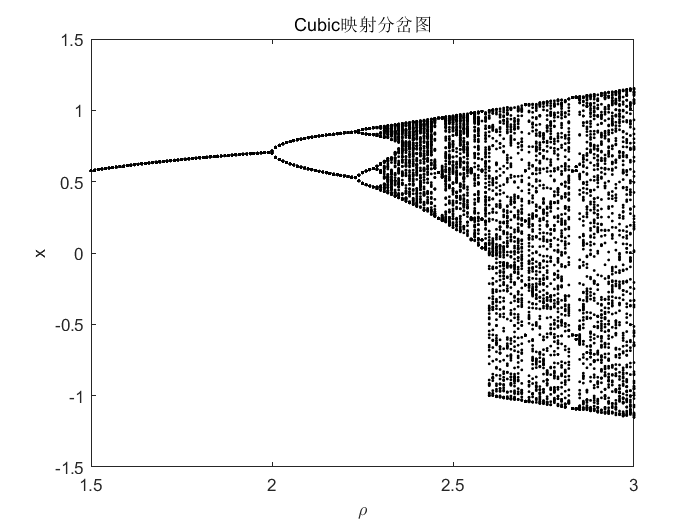
6、Cubic映射

Cubic映射是密码学等各种应用中产生混沌序列最常用的映射之一，其定义如下：$$x_{n+1}=\rho x_n(1-x_n^2)\text{\hspace{1em}(5)}$$其中，$\rho$是映射因子。

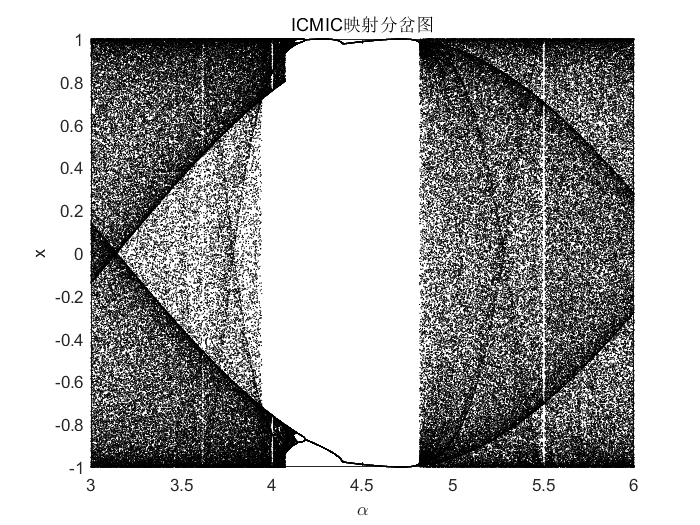
7、ICMIC映射

迭代无限折叠混沌映射(ICMIC)在$(-1,1)$中生成混沌序列，其定义如下：$$x_{n+1}=\sin \left(\frac{\alpha }{x_n}\right),\alpha \in (0,+\infty ),x_n\in (-1,1)\text{\hspace{1em}(6)}$$或者：$$x_{n+1}=\sin \left(\frac{\alpha \pi }{x_n}\right),\alpha \in (0,1),x_n\in (-1,1)\text{\hspace{1em}(7)}$$

二、仿真实验

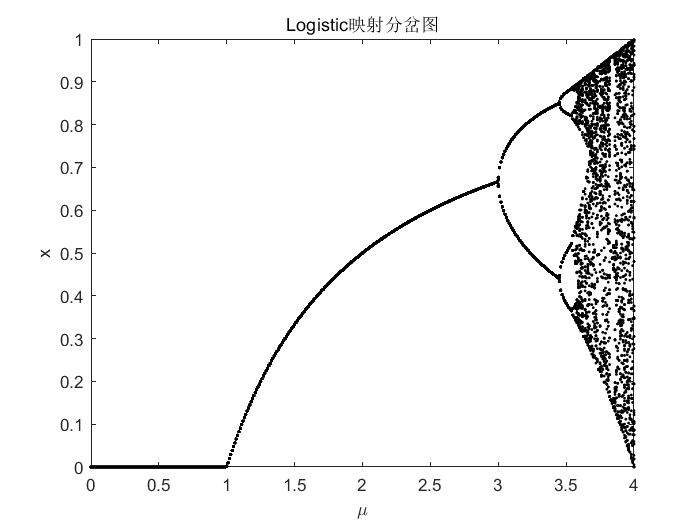
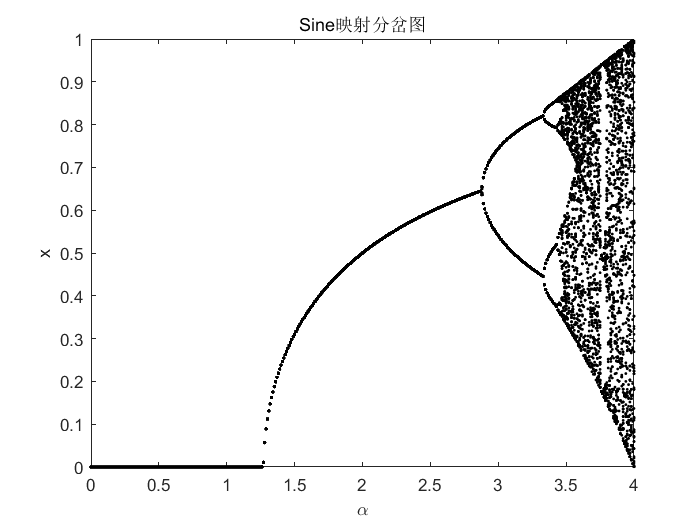
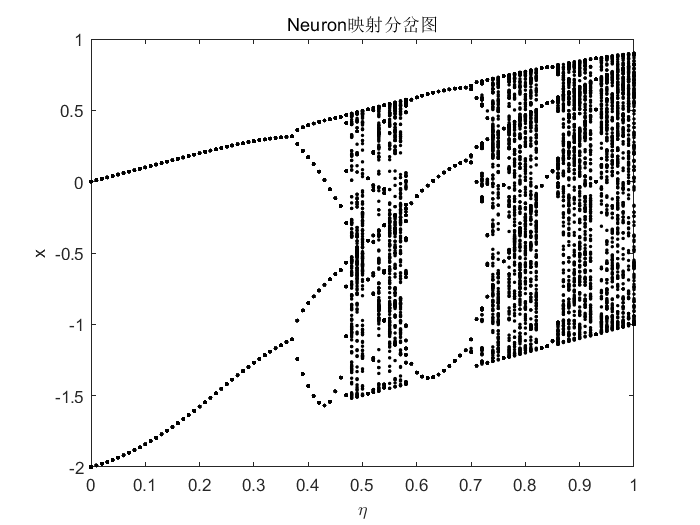
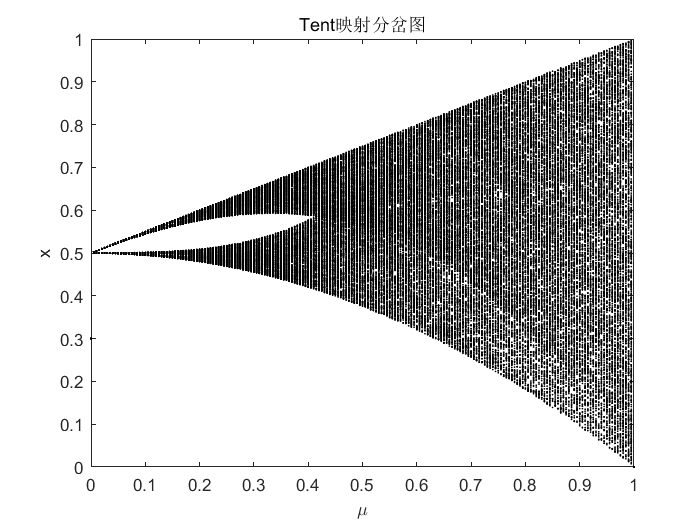
代码下载链接：https://download.csdn.net/download/weixin_43821559/85221680

三、参考文献

[1] Feng, J., Zhang, J., Zhu, X. et al. A novel chaos optimization algorithm[J]. Multimedia Tools and Applications, 2017, 76: 17405-17436.

最后

以上就是怕黑咖啡豆为你收集整理的混沌映射分岔图一、理论基础二、仿真实验三、参考文献的全部内容，希望文章能够帮你解决混沌映射分岔图一、理论基础二、仿真实验三、参考文献所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。