介绍：

BCD（Binary-Coded Decimal）码，也叫二-十进制码，主要就是用4位二进制数来表示1位的从0~9的十进制数。

BCD码主要分为有权码（8421码，5421码，2421码）和无权码（余3码，余3循环码），这篇文章将主要介绍有权码中的8421码。

功能：

在一次编程练习中，需要分别提取出十进制数的个，十，百，千位。通过BCD码可以实现此功能。

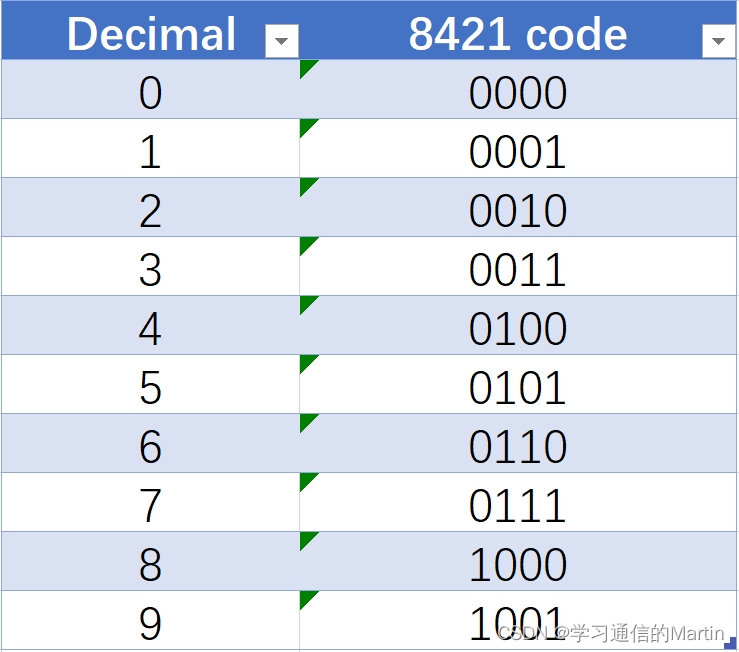
二进制和十进制数字对照：

从二进制和十进制数字对照十分简单，就像原理所说的：用指定的4位二进制数来表示1位的从0~9的十进制数。对照表格即可：

换算算法：

8421码主要有两种换算算法，从二进制到十进制（B to D），从十进制到二进制（D to B）。

B to D：

从二进制转换到十进制需要用到权值8421来进行计算。只需要将8，4，2，1分别与二进制中的四位相乘后再相加，就能得到十进制对应的数字，如下表所示：

红色字体为二进制的8421码。 

D to B：

将十进制数编码成二进制数的过程相对复杂一点，我总结了一下，并把过程分为三个步骤，但是其中两个步骤是同级进行的。

1. 补0

在像转换的十进制数的二进制数前面，补上十进制数的位数乘以4的0。举个例子（下面都以这个为例子），我现在需要转换的十进制数是103，二进制为110 0111。此时十进制数的位数为3，所以我们就要在110 0111前补上3*4=12个0，一共3组。所以我们就能得到：

0000 0000 0000 110 0111

2. 移位&判断

得到补0后的数，需要把原数进行左移，并且每左移一次判断一次，哪一组0大于4，就将那组的二进制数+3（in Decimal）后，再进行移位；如果所有组的二进制数都小于或者等于4，就进行下一次移位。

直到将原数的7位（例子103）全部移位完，输出数据。

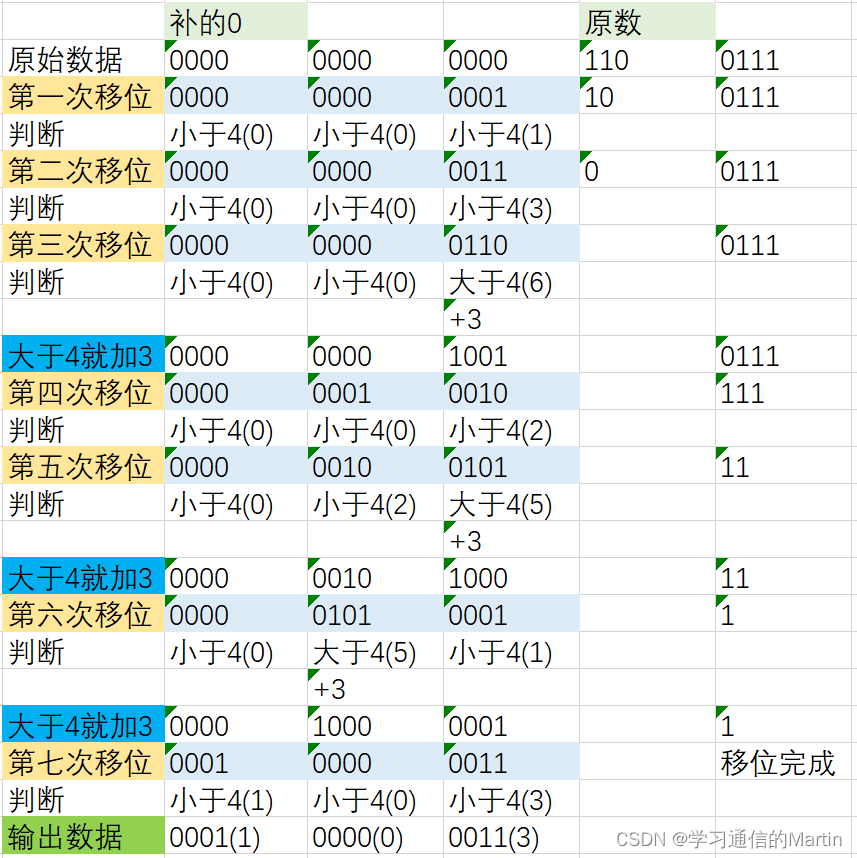
 由图可知，输出的数据正确。

并且我只需要4位4位的提取，就能清楚的知道这个数的个位，十位和百位，来进行我想要的操作。

最后

以上就是暴躁服饰为你收集整理的BCD码：8421码介绍：功能：二进制和十进制数字对照：换算算法：的全部内容，希望文章能够帮你解决BCD码：8421码介绍：功能：二进制和十进制数字对照：换算算法：所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。