十进制

• 珠算盘就是一个十进制计数器，任何一个数都可以用0，1，2，3，4，5，6，7，8，9这10个数码中的一个或几个，按照一定的规律排列起来表示，其计数规律“逢十进一”。
• 10=1×10¹+0×10⁰，以10为基数的计数体制。
• 如4587.29可以表示为：4587.29=4×10³+5×10²+8×10¹+7×10⁰+2×10^-1+9×10^-2，其中10³、10²、10¹、10⁰分别为千位、百位、十位和各位数码的权，而小数点以右数码的权值是负幂。
• 一般地说，任意十进制数可以表示为：$$(N{)}_D=\sum _{i=-\infty }^{\infty }{K}_i\times 10^i$$
• D(Decimal)表示十进制。
• 扩展
  • 把10用R代替，可以得到任意进制数的表达式： $$(N{)}_D=\sum _{i=-\infty }^{\infty }{K}_i\times R^i$$
  • $K_i$是$i$次幂的系数，根据基数$R$的不同，它的取值为0到R-1个不同的数码。如对于十进制数，$R$为10，所以$K_i$的取值为0~9共10个数码。
• 数字电路不便于存储或处理十进制数。构成数字电路的基本思路是把电路的状态和数码对应起来。二进制只有0与1两个数码，分别用数字电路的两种状态来表示。十进制的10个数码就要求电路有10个完全不同的状态，这使得电路非常复杂。

二进制

• 二进制中，只有0与1两个数码，计数规律“逢二进一”，即1+1=10=1×2¹+0×2⁰。
• 二进制是以2为基数的计数体制。任意二进制数可表示为：$$(N{)}_B=\sum _{i=-\infty }^{\infty }{K}_i\times 2^i$$
• $K_i$为基数“2”的第$i$次幂的系数，它可以是“0”或者“1”。
• 将二进制数(1010110)_B转为十进制数：
  • (1010110)_B=1×2⁶+0×2⁵+1×2⁴+0×2³+1×2²+1×2¹+0×2⁰=(86)_D
• 优点：
  • 数字电路简单可靠，所用元件少。
  • 基本运算规则简单，运算操作方便。
• 缺点：有的数位数太多，不便于书写与阅读，使用不方便。
• 在送入计算机时，计算机先将十进制数转换成数字系统能接受的二进制数；在运算结束后，再将二进制数转换为十进制数，输出十进制结果。

二进制的四则运算

• 加法运算
  • “逢二进一”，运算规律如：0+0=0，0+1=1，1+0=1，1+1=10.
  • 当遇到“1+1”时就向相邻高位进1.
    
• 减法运算
  • “借一当二”， 运算规律如：0-0=0，1-0=1，1-1=0，10-1=1.
  • 当遇到“0-1”时，需向高位借1当2用。
    
• 乘法运算
  • “各数相乘，再作加法运算”， 运算规律如：0×0=0，1×0=0，0×1=0，1×1=1.
    
• 除法运算
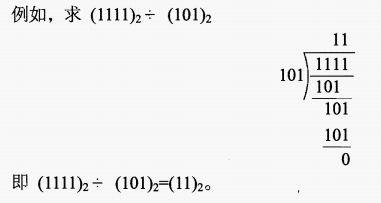
  • “各数相除，再作减法运算”，运算规律如：0÷1=0， 1÷1=1.
    

二进制的波形表示

• 二值数据常用数字波形来表示，用二进制表示0~15
  
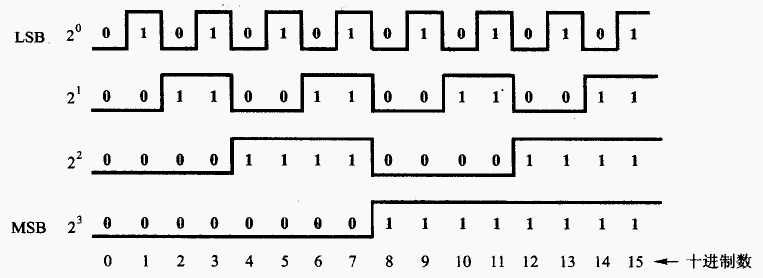
• 最左列标出二进制数的位权（2⁰、2¹、2²），最低位（Least Significant Bit, LSB），最高位（Most Significant Bit, MSB），最后一行标出等效的0~15的十进制数。

二进制数据的传输

• 二进制数据从一处传输到另一处，可以采用串行的方式或并行的方式。
• 串行方式：
  • 一组数据在时钟脉冲的控制下逐位传送。
  • 所需设备简单，只需一根导线和一共同接地端既可。
  • 两台计算机之间，或计算机通过电话线与网络连接均采用这种方式。
    
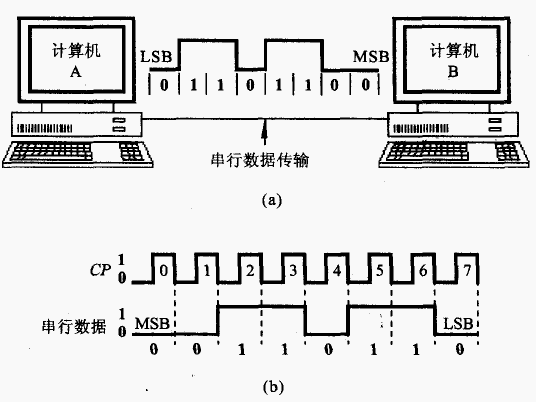
  • 在时钟脉冲的控制下，数据由最高位MSB到最低位LSB依次传输。每传送一位数需要一个时钟周期，并且在时钟脉冲的下降沿完成。
• 并行传输：
  • 传输速度快，将一组二进制数据同时传输。
  • 所需设备复杂，需要多条传输线和其他部件。
  • 并行传输在数字系统中是常用的技术。
    
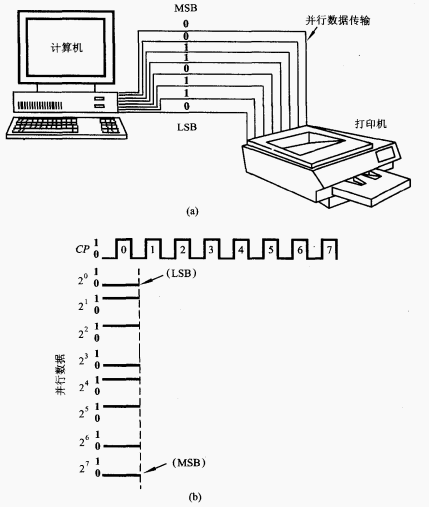
  • 如图，需要8根传输线。传输8位数据所需的时间是一个时钟脉冲的周期，只有串行传输时间的1/8。

十六进制数

• 十六进制数有16个数码：0，1，2，3，4，5，6，7，8，9，A(10)，B(11)，C(12)，D(13)，E(14)，F(15)。
• 逢十六进一。
• (3A6.D)₁₆=3×16²+10×16¹+6×16⁰+13×16^-1.
• 十六进制常用字母H表示，故(3A6.D)₁₆=(3A6.D)_H。

数制转换

• 二进制转十进制

  • 将二进制数各位数码与位权相乘后求和。
  • (101.1)₂=1×2²+0×2¹+1×2⁰+1×2^-1=4+0+1+0.5=(5.5)₁₀

• 十进制转二进制

  • 采用除2取余法，即将十进制数依次除2，并依次记下余数，一直除到商数为0，最后把全部余数按相反次序排列，就能得到二进制数。
    
    

• 二进制转十六进制

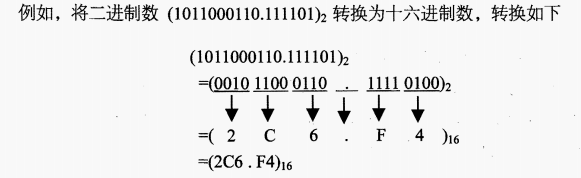
  • 从小数点起向左、右按4位分组，不足4位的，整数部分可在最高位的左边加0补齐，小数点部分不足4位的，可在最低位右边加0补齐，每组以其对应的十六进制数代替，将各个十六进制数依次写出。
    
    

• 十六进制数转二进制数

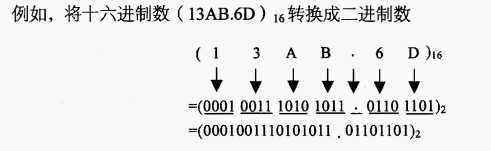
  • 从左到右将待转换的十六进制数中的每个数依次用4位二进制数表示。
    

最后

以上就是外向牛排为你收集整理的数字电路学习笔记（二）十进制二进制二进制的四则运算二进制的波形表示二进制数据的传输十六进制数数制转换的全部内容，希望文章能够帮你解决数字电路学习笔记（二）十进制二进制二进制的四则运算二进制的波形表示二进制数据的传输十六进制数数制转换所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。