本篇文章是对论文《Domain Adaptation via Transfer
Component Analysis》进行学习
1 背景
首先我们引入域的概念,通常认为域由两部分组成:输入
χ
chi
χ的特征空间和输入X的边缘概率分布P(X),其中
X
=
(
x
1
,
x
2
,
.
.
.
,
x
n
)
∈
χ
X=(x_{1},x_{2},...,x_{n})in chi
X=(x1,x2,...,xn)∈χ是输入样本。一般而言,如果两个域不同,那么它们有着不同的特征空间或者不同的边缘概率分布。
我们假设
D
S
=
D_{S}=
DS={
(
x
S
1
,
y
S
1
)
,
(
x
S
2
,
y
S
2
)
,
.
.
.
,
(
x
S
n
1
,
y
S
n
1
)
(x_{S_{1}},y_{S_{1}}),(x_{S_{2}},y_{S_{2}}),...,(x_{S_{n_{1}}},y_{S_{n_{1}}})
(xS1,yS1),(xS2,yS2),...,(xSn1,ySn1)},
D
T
=
D_{T}=
DT={
x
T
1
,
x
T
2
,
.
.
.
,
x
T
n
2
x_{T_{1}},x_{T_{2}},...,x_{T_{n_{2}}}
xT1,xT2,...,xTn2},
P
(
X
S
)
P(X_{S})
P(XS)为
D
S
D_{S}
DS的边缘概率分布,
Q
(
X
T
)
Q(X_{T})
Q(XT)为
D
T
D_{T}
DT的边缘概率分布,其中
D
S
D_{S}
DS和
D
T
D_{T}
DT的特征空间是一致的,但边缘概率分布
P
(
X
S
)
P(X_{S})
P(XS)和
Q
(
X
T
)
Q(X_{T})
Q(XT)不一致。
我们将
D
S
D_{S}
DS称为源域,将
D
T
D_{T}
DT称为目标域,可以看到源域中的数据为已标注数据,目标域为未标注数据。那么有这样一类问题:是否可以在源域上训练分类器,然后用得到的分类器目标域上对未标注数据进行标注。
大多数域适应方法处理此问题时会假设
P
(
X
S
)
≠
Q
(
X
T
)
P(X_{S})neq Q(X_{T})
P(XS)=Q(XT),
P
(
Y
S
∣
X
S
)
=
Q
(
Y
T
∣
X
T
)
P(Y_{S}|X_{S})=Q(Y_{T}|X_{T})
P(YS∣XS)=Q(YT∣XT),但实际场景中,不同域的条件概率分布有时也是不同的。此时TCA被提出来,TCA进行了更弱的假设,就是
P
(
X
S
)
≠
Q
(
X
T
)
P(X_{S})neq Q(X_{T})
P(XS)=Q(XT),但存在一个映射
ϕ
phi
ϕ(注意
ϕ
phi
ϕ通常是非线性的)使得
P
(
ϕ
(
X
S
)
)
≈
Q
(
ϕ
(
X
T
)
)
P(phi (X_{S}))approx Q(phi (X_{T}))
P(ϕ(XS))≈Q(ϕ(XT))且
P
(
Y
S
∣
ϕ
(
X
S
)
)
≈
Q
(
Y
T
∣
ϕ
(
X
T
)
)
P(Y_{S}|phi (X_{S}))approx Q(Y_{T}|phi (X_{T}))
P(YS∣ϕ(XS))≈Q(YT∣ϕ(XT)),那么接下来的关键就是找到这样的映射
ϕ
phi
ϕ。
2 知识准备
在正式开始学习TCA前,先引入两个概念。(参照https://zhuanlan.zhihu.com/p/27305237)
2.1 MMD距离
MMD全称是 Maximum Mean Discrepancy,用于在再生核希尔伯特空间中度量两个分布的距离。
下面举个例子,假设X=(
x
1
,
x
2
,
.
.
.
,
x
n
1
x_{1},x_{2},...,x_{n_{1}}
x1,x2,...,xn1),Y=(
y
1
,
y
2
,
.
.
.
,
y
n
2
y_{1},y_{2},...,y_{n_{2}}
y1,y2,...,yn2)是从两个不同的分布进行采样得到的样本集,那么
MMD(X,Y)=
∣
∣
1
n
1
∑
i
=
1
n
1
ϕ
(
x
i
)
−
1
n
2
∑
i
=
1
n
2
ϕ
(
y
i
)
∣
∣
2
||frac{1}{n_{1}}sum_{i=1}^{n_{1}}phi (x_{i})-frac{1}{n_{2}}sum_{i=1}^{n_{2}}phi (y_{i})||^{2}
∣∣n11∑i=1n1ϕ(xi)−n21∑i=1n2ϕ(yi)∣∣2,其中
ϕ
phi
ϕ是向希尔伯特空间进行映射的函数,通过这个式子很容易看出,MMD距离就是样本在高维空间的映射的均值之间的距离。
注意,当且仅当两个分布相同时,MMD距离趋近于零。
2.2 HSIC
HSIC的全称是Hilbert–Schmidt Independence Criterion,希尔伯特-施密特独立性系数,用于度量两个样本集之间的独立性。
HSIC(X,Y)=
1
(
n
−
1
)
2
t
r
(
H
K
H
K
y
y
)
frac{1}{(n-1)^{2}}tr(HKHK_{yy})
(n−1)21tr(HKHKyy)
其中
n
=
n
1
+
n
2
n=n_{1}+n_{2}
n=n1+n2,
H
=
I
−
1
n
I
I
H=I-frac{1}{n}II
H=I−n1II(
I
I
I为单位矩阵,
I
I
II
II为元素全为1的矩阵),H用于中心化,
K
K
K和
K
y
y
K_{yy}
Kyy为X和Y的核矩阵。
HSIC(X,Y)的值越大,表明X和Y的依赖性越强。
3 无监督TCA
3.1 问题转化
前面提到TCA假设
P
(
X
S
)
≠
Q
(
X
T
)
P(X_{S})neq Q(X_{T})
P(XS)=Q(XT),但存在一个映射
ϕ
phi
ϕ使得
P
(
ϕ
(
X
S
)
)
≈
Q
(
ϕ
(
X
T
)
)
P(phi (X_{S}))approx Q(phi (X_{T}))
P(ϕ(XS))≈Q(ϕ(XT))且
P
(
Y
S
∣
ϕ
(
X
S
)
)
≈
Q
(
Y
T
∣
ϕ
(
X
T
)
)
P(Y_{S}|phi (X_{S}))approx Q(Y_{T}|phi (X_{T}))
P(YS∣ϕ(XS))≈Q(YT∣ϕ(XT))。
那么接下来的关键就是找到这样的映射
ϕ
phi
ϕ,但需要注意的是目标域上的数据是没有标签的,也就是
Q
(
Y
T
∣
ϕ
(
X
T
)
)
Q(Y_{T}|phi (X_{T}))
Q(YT∣ϕ(XT))一开始是不知道的,那么就不能直接通过最小化
P
(
Y
S
∣
ϕ
(
X
S
)
P(Y_{S}|phi (X_{S})
P(YS∣ϕ(XS)和
Q
(
Y
T
∣
ϕ
(
X
T
)
)
Q(Y_{T}|phi (X_{T}))
Q(YT∣ϕ(XT))的距离来学习映射
ϕ
phi
ϕ。
文章中又换了一个思路,既然不能直接最小化
P
(
Y
S
∣
ϕ
(
X
S
)
P(Y_{S}|phi (X_{S})
P(YS∣ϕ(XS)和
Q
(
Y
T
∣
ϕ
(
X
T
)
)
Q(Y_{T}|phi (X_{T}))
Q(YT∣ϕ(XT)),那么就换个方式同样实现这样的效果,就是接下来的两个条件:
(1)最小化
P
(
ϕ
(
X
S
)
)
P(phi (X_{S}))
P(ϕ(XS))和
Q
(
ϕ
(
X
T
)
)
Q(phi (X_{T}))
Q(ϕ(XT))之间的距离;
(2)
ϕ
(
X
S
)
phi (X_{S})
ϕ(XS)和
ϕ
(
X
T
)
phi (X_{T})
ϕ(XT)保留了
X
S
X_{S}
XS和
X
T
X_{T}
XT的一些重要属性;
满足这两个条件后,就可以假设
P
(
Y
S
∣
ϕ
(
X
S
)
)
≈
Q
(
Y
T
∣
ϕ
(
X
T
)
)
P(Y_{S}|phi (X_{S}))approx Q(Y_{T}|phi (X_{T}))
P(YS∣ϕ(XS))≈Q(YT∣ϕ(XT)),此时在
ϕ
(
X
S
)
phi (X_{S})
ϕ(XS)和
Y
S
Y_{S}
YS上训练得到的分类器f就可以在
ϕ
(
X
T
)
phi (X_{T})
ϕ(XT)上使用。
3.2 最小化 P ( ϕ ( X S ) ) P(phi (X_{S})) P(ϕ(XS))和 Q ( ϕ ( X T ) ) Q(phi (X_{T})) Q(ϕ(XT))之间的距离
在这里我们用MMD距离来衡量两个域的边缘概率分布之间的距离,因为当MMD距离趋近于0时两个分布相同,这在前面也用黑体字进行加粗。
那么
P
(
ϕ
(
X
S
)
)
P(phi (X_{S}))
P(ϕ(XS))和
Q
(
ϕ
(
X
T
)
)
Q(phi (X_{T}))
Q(ϕ(XT))之间的距离可以用下式进行衡量:
M
M
D
(
X
S
,
X
T
)
=
∣
∣
1
n
1
∑
i
=
1
n
1
ϕ
(
x
S
i
)
−
1
n
2
∑
i
=
1
n
2
ϕ
(
x
T
i
)
∣
∣
2
MMD(X_{S},X_{T})=||frac{1}{n_{1}}sum_{i=1}^{n_{1}}phi (x_{S_{i}})-frac{1}{n_{2}}sum_{i=1}^{n_{2}}phi (x_{T_{i}})||^{2}
MMD(XS,XT)=∣∣n11∑i=1n1ϕ(xSi)−n21∑i=1n2ϕ(xTi)∣∣2
但直接最小化该式来求解
ϕ
phi
ϕ很容易陷入局部极小值,此时我们不直接显式求解
ϕ
phi
ϕ,先考虑下面的这个方法。
3.2.1 MMDE
MMDE是一种基于降维的域适应方法,该方法通过
ϕ
phi
ϕ将源域数据和目标域数据进行映射后,通过解决一个半定规划问题来学习对应的核矩阵K,最后再降维到一个共享的低维的潜在空间。
K
=
[
K
S
,
S
K
S
,
T
K
T
,
S
K
T
,
T
]
K=begin{bmatrix} K_{S,S} &K_{S,T} \ K_{T,S} &K_{T,T} end{bmatrix}
K=[KS,SKT,SKS,TKT,T]
其中
K
S
,
S
K_{S,S}
KS,S,
K
T
,
T
K_{T,T}
KT,T是源域和目标域上的核矩阵,
K
S
,
T
,
K
T
,
S
K_{S,T},K_{T,S}
KS,T,KT,S是跨域的核矩阵,K的大小是
(
n
1
+
n
2
)
∗
(
n
1
+
n
2
)
(n_{1}+n_{2})*(n_{1}+n_{2})
(n1+n2)∗(n1+n2)
另外我们定义
(
n
1
+
n
2
)
∗
(
n
1
+
n
2
)
(n_{1}+n_{2})*(n_{1}+n_{2})
(n1+n2)∗(n1+n2)的矩阵L,其中
当
x
i
,
x
j
∈
X
S
x_{i},x_{j}in X_{S}
xi,xj∈XS时,
L
i
,
j
=
1
n
1
2
L_{i,j}=frac{1}{n_{1}^{2}}
Li,j=n121;
当
x
i
,
x
j
∈
X
T
x_{i},x_{j}in X_{T}
xi,xj∈XT时,
L
i
,
j
=
1
n
2
2
L_{i,j}=frac{1}{n_{2}^{2}}
Li,j=n221;
否则,
L
i
,
j
=
−
1
n
1
n
2
L_{i,j}=-frac{1}{n_{1}n_{2}}
Li,j=−n1n21;
那么
M
M
D
(
X
S
,
X
T
)
=
t
r
(
K
L
)
MMD(X_{S},X_{T})=tr(KL)
MMD(XS,XT)=tr(KL)。
我们的任务是最小化MMD距离,同时还要保留
X
S
X_{S}
XS和
X
T
X_{T}
XT的一些重要属性,后面这一点可以体现为最大化
ϕ
(
X
S
)
phi (X_{S})
ϕ(XS)和
ϕ
(
X
T
)
phi (X_{T})
ϕ(XT)的方差(这点后续过程会有解释),上述目标可以体现为下述问题:
min
t
r
(
K
L
)
−
λ
t
r
(
K
)
min tr(KL)-lambda tr(K)
mintr(KL)−λtr(K)
其中K是正定矩阵,tr(K)表示的是
ϕ
(
X
S
)
phi (X_{S})
ϕ(XS)和
ϕ
(
X
T
)
phi (X_{T})
ϕ(XT)的方差,
λ
lambda
λ是权衡参数。
这里会有个疑问,是否真的存在一个核函数与学到的矩阵K是对应的?这里有个定理:

这也是为什么上面的目标函数要求K是正定的。
当核矩阵K确定后,那么其对应的
ϕ
phi
ϕ就确定了,但这个
ϕ
phi
ϕ并不是显式的,不能直接利用,那我们就不求解
ϕ
phi
ϕ,借助KPCA对K进行特征值分解,直接进行降维,这样就可以得到一个共享的低维的潜在空间。将源域数据和目标域数据映射到该潜在空间后便可在源域数据上训练分类器,然后将训练好的分类器应用到目标域数据。
现在看来问题解决了,但MMDE存在几个缺陷:
(1)MMDE只能针对源域和目标域进行处理,如果再来一个目标域,那么就需要重新计算核矩阵K,然后特征值分解,所以不具备向未知样本的泛化能力;
(2)求解K时需要用到半定规划,计算代价比较高;
(3)后续进行降维时需要用到KPCA,这样可能会损失原数据
X
S
X_{S}
XS和
X
T
X_{T}
XT的一些重要属性,就是说进行大量计算求解到的核矩阵保留了一些重要属性,然后后面降维的时候可能会损失掉了;
3.2.2 参数化核映射
与MMDE求解核矩阵不同,参数化核映射则是直接定义核函数,然后根据样本计算得到核矩阵K,K的维数还是
(
n
1
+
n
2
)
∗
(
n
1
+
n
2
)
(n_{1}+n_{2})*(n_{1}+n_{2})
(n1+n2)∗(n1+n2)。
我们用下面的形式表示K:
K
=
(
K
K
−
1
2
)
(
K
−
1
2
K
)
K=(KK^{-frac{1}{2}})(K^{-frac{1}{2}}K)
K=(KK−21)(K−21K),此处使用了经验核映射
ϕ
′
(
x
i
)
=
K
−
1
/
2
K
i
phi ^{'}(x_{i})=K^{-1/2}K_{i}
ϕ′(xi)=K−1/2Ki(可以参照我的另一篇博客进行理解:https://blog.csdn.net/qq_40824311/article/details/102636765,只看经验核映射那一节即可),经验核映射将样本映射到
(
n
1
+
n
2
)
(n_{1}+n_{2})
(n1+n2)上。
我们引入矩阵
W
~
∈
R
(
n
1
+
n
2
)
∗
m
widetilde{W}in R^{(n_{1}+n_{2})*m}
W
∈R(n1+n2)∗m,其中
m
≪
(
n
1
+
n
2
)
mll (n_{1}+n_{2})
m≪(n1+n2),该矩阵将经验核映射后的样本降到m维。
我们将
W
~
widetilde{W}
W
嵌入到K中得:
K
~
=
(
K
K
−
1
2
W
~
)
(
W
~
T
K
−
1
2
K
)
=
K
W
W
T
K
T
widetilde{K}=(KK^{-frac{1}{2}}widetilde{W})(widetilde{W}^{T}K^{-frac{1}{2}}K)=KWW^{T}K^{T}
K
=(KK−21W
)(W
TK−21K)=KWWTKT,其中
W
=
K
−
1
2
W
~
W=K^{-frac{1}{2}}widetilde{W}
W=K−21W
,此时的
K
~
widetilde{K}
K
就是我们最终的参数化核矩阵,将该矩阵替换上一节式
M
M
D
(
X
S
,
X
T
)
=
t
r
(
K
L
)
MMD(X_{S},X_{T})=tr(KL)
MMD(XS,XT)=tr(KL)中的K,就可以得到
M
M
D
(
X
S
,
X
T
)
=
t
r
(
K
W
W
T
K
T
L
)
=
t
r
(
K
W
L
W
T
K
T
)
MMD(X_{S},X_{T})=tr(KWW^{T}K^{T}L)=tr(KWLW^{T}K^{T})
MMD(XS,XT)=tr(KWWTKTL)=tr(KWLWTKT),对该式进行最小化,即可减小两个域在最终低维潜在空间的距离,注意要加上正则项
t
r
(
W
T
W
)
tr(W^{T}W)
tr(WTW),以限制W的复杂度。
论文中,TCA采用了这种方法。
3.2.3 参数化核映射与MMDE的区别
MMDE开始时没有给定核函数,而是通过一个SDP问题得到核矩阵,该核矩阵要求是正定的,因此存在与之对应的核函数,此时核函数才确定了下来;而TCA的方法则是先给定核函数,然后根据核函数直接获得核矩阵。这两种做法有着本质的区别,MMDE中的方法一开始没给定核函数,就意味着没有确定映射
ϕ
phi
ϕ,那么求解核矩阵实际上就是求解相应的映射
ϕ
phi
ϕ,这样得到的映射
ϕ
phi
ϕ使得
ϕ
(
X
S
)
phi (X_{S})
ϕ(XS)和
ϕ
(
X
T
)
phi (X_{T})
ϕ(XT)的分布是相近的。而TCA中一开始就给定了核函数,那么映射
ϕ
phi
ϕ就已经确定了,那么
ϕ
(
X
S
)
phi (X_{S})
ϕ(XS)和
ϕ
(
X
T
)
phi (X_{T})
ϕ(XT)分布就不能保证是相近的。从这个角度来看,MMDE的效果是更优的。
但MMDE的缺点上面也有提到,而参数化核映射中则避免了这些问题。
(1)MMDE不具备向未知样本的泛化能力
TCA中对参数化核映射进行求解后,可以得到W。当又来一组样本
X
′
=
(
x
1
′
,
x
2
′
,
.
.
.
,
x
l
′
)
X^{'}=(x_{1}^{'},x_{2}^{'},...,x_{l}^{'})
X′=(x1′,x2′,...,xl′)后,对其中的任意一个样本
x
i
′
x_{i}^{'}
xi′可以通过以下操作向低维潜在空间进行映射:
(
K
(
x
i
′
,
x
S
n
1
)
,
K
(
x
i
′
,
x
S
n
1
)
,
.
.
.
,
K
(
x
i
′
,
x
S
n
1
)
,
K
(
x
i
′
,
x
T
1
)
,
K
(
x
i
′
,
x
T
2
)
,
.
.
.
,
K
(
x
i
′
,
x
T
n
2
)
)
W
(K(x_{i}^{'},x_{S_{n_{1}}}),K(x_{i}^{'},x_{S_{n_{1}}}),...,K(x_{i}^{'},x_{S_{n_{1}}}),K(x_{i}^{'},x_{T_{1}}),K(x_{i}^{'},x_{T_{2}}),...,K(x_{i}^{'},x_{T_{n_{2}}}))W
(K(xi′,xSn1),K(xi′,xSn1),...,K(xi′,xSn1),K(xi′,xT1),K(xi′,xT2),...,K(xi′,xTn2))W,也就是先通过
x
i
′
x_{i}^{'}
xi′和源域、目标域中的数据进行核函数运算映射到
(
n
1
+
n
2
)
(n_{1}+n_{2})
(n1+n2)维上,然后用W降维到低维空间。
MMDE是不能通过这样的操作对未知样本进行泛化,虽然MMDE学到了核矩阵K,K也确定了核函数,但这个核函数并没有显式定义,因此无法计算K(x,y)。
(2)MMDE进行了SDP,运算代价高
在文章的后面可以看到,参数化核映射的方法避免了SDP问题。
(3)MMDE后续进行了KPCA,可能会损失数据中一些重要的属性
上面提到MMDE先学习核矩阵,然后用KPCA进行降维;而参数化核映射则是将核矩阵和降维矩阵W合并在一起,论文中将参数化核映射时有一句话“ instead of using a two-step approach as in MMDE”讲的就是这个。上面也提到参数化核映射中核函数一开始就是给定的,那么一开始的映射
ϕ
phi
ϕ并不能把源域和目标域映射到分布相近的空间中,而是在用W进行降维的过程中实现的,也就是一边优化映射(参数化核映射),一边进行降维,那么就不会出现损失数据属性的问题。
3.3 保留 X S X_{S} XS和 X T X_{T} XT的属性
在域适应问题中,不能仅通过最小化
P
(
ϕ
(
X
S
)
)
P(phi (X_{S}))
P(ϕ(XS))和
Q
(
ϕ
(
X
T
)
)
Q(phi (X_{T}))
Q(ϕ(XT))之间的距离来学习映射,下面举个例子:
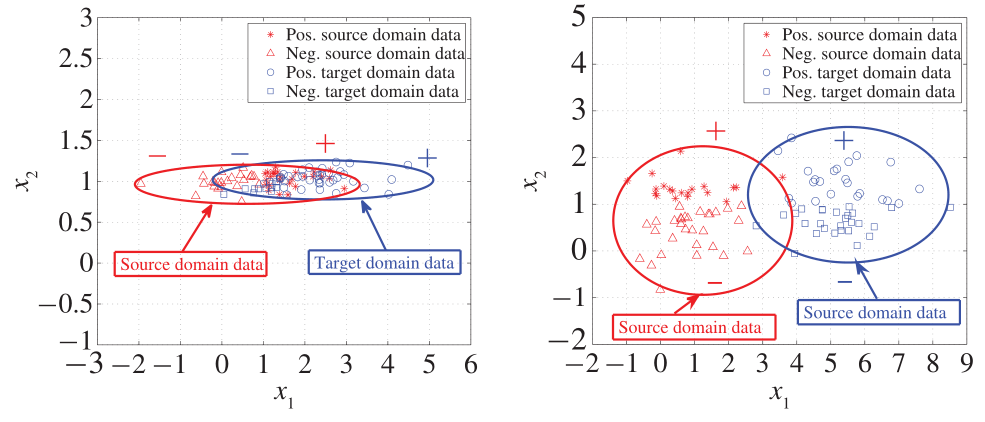
在上面的左侧图片中,红色为源域,蓝色为目标域,我们把每个样本看做两维
(
x
1
,
x
2
)
T
(x_{1},x_{2})^{T}
(x1,x2)T,其中
x
1
x_{1}
x1可以用于区分正负样本,
x
2
x_{2}
x2则为噪声,方差一般较小。如果仅最小化
P
(
ϕ
(
X
S
)
)
P(phi (X_{S}))
P(ϕ(XS))和
Q
(
ϕ
(
X
T
)
)
Q(phi (X_{T}))
Q(ϕ(XT))之间的距离,那么很明显会导致数据映射到
x
1
x_{1}
x1所在维,而这个空间上的数据是不能用于区分进行分类。上面的例子就说明了寻找映射时,不仅要最小化
P
(
ϕ
(
X
S
)
)
P(phi (X_{S}))
P(ϕ(XS))和
Q
(
ϕ
(
X
T
)
)
Q(phi (X_{T}))
Q(ϕ(XT))之间的距离,也要注意保留对分类任务有用的属性,一个选择就是最大化映射后的数据的方差。从上面的推导可以看出,样本集X在低维潜在空间的映射是
W
T
K
W^{T}K
WTK,其中样本
x
i
x_{i}
xi对应
W
T
K
W^{T}K
WTK的第i列,可以得出样本在低维潜在空间上的方差是
W
T
K
H
K
W
W^{T}KHKW
WTKHKW,其中H是中心化矩阵,
H
=
I
n
1
+
n
2
−
1
n
1
+
n
2
H=I_{n_{1}+n_{2}}-frac{1}{n_{1}+n_{2}}
H=In1+n2−n1+n2111,11是
(
n
1
+
n
2
)
∗
(
n
1
+
n
2
)
(n_{1}+n_{2})*(n_{1}+n_{2})
(n1+n2)∗(n1+n2)的全为1的矩阵。
那么这时候会有一个疑问,能不能只最大化地保留数据的方差,上面的右侧图片中可以看出,仅最大化映射后数据的方差,会保留
x
1
x_{1}
x1维,在该维上
P
(
ϕ
(
X
S
)
)
P(phi (X_{S}))
P(ϕ(XS))和
Q
(
ϕ
(
X
T
)
)
Q(phi (X_{T}))
Q(ϕ(XT))之间的距离较大,且不能用于分类任务。
3.4 无监督TCA推导
3.2节中讲了最小化
P
(
ϕ
(
X
S
)
)
P(phi (X_{S}))
P(ϕ(XS))和
Q
(
ϕ
(
X
T
)
)
Q(phi (X_{T}))
Q(ϕ(XT))之间距离的目标函数,3.3节讲了保留数据属性的方法,现在我们把两点结合起来就可以形成TCA的目标函数:
m
i
n
W
t
r
(
W
T
K
L
K
W
)
+
μ
t
r
(
W
T
W
)
min_{W} tr(W^{T}KLKW)+mu tr(W^{T}W)
minWtr(WTKLKW)+μtr(WTW)
s
.
t
.
W
T
K
H
K
W
=
I
m
s.t. W^{T}KHKW=I_{m}
s.t.WTKHKW=Im(注1)
这个问题并不是个凸优化问题,但仍然可以高效的解决。首先通过拉格朗日乘子法可得:
m
i
n
W
t
r
(
W
T
(
K
L
K
+
μ
I
)
W
)
−
t
r
(
(
W
T
K
H
K
W
−
I
)
Z
)
min_{W}tr(W^{T}(KLK+mu I)W)-tr((W^{T}KHKW-I)Z)
minWtr(WT(KLK+μI)W)−tr((WTKHKW−I)Z)(1),其中Z是一个对角矩阵,对角线上每个元素都是一个拉格朗日乘子。
对W进行求导得:
(
K
L
K
+
μ
I
)
W
=
K
H
K
W
Z
(KLK+mu I)W=KHKWZ
(KLK+μI)W=KHKWZ
⇒
Z
=
(
K
H
K
W
)
−
1
(
K
L
K
+
μ
I
)
W
Rightarrow Z=(KHKW)^{-1}(KLK+mu I)W
⇒Z=(KHKW)−1(KLK+μI)W
将Z代回式(1)中得:
m
i
n
W
t
r
(
(
K
H
K
W
)
−
1
(
K
L
K
+
μ
I
)
W
)
min_{W}tr((KHKW)^{-1}(KLK+mu I)W)
minWtr((KHKW)−1(KLK+μI)W)
=
m
i
n
W
t
r
(
W
−
1
(
K
H
K
)
−
1
(
K
L
K
+
μ
I
)
W
)
=min_{W}tr(W^{-1}(KHK)^{-1}(KLK+mu I)W)
=minWtr(W−1(KHK)−1(KLK+μI)W)
=
m
a
x
W
t
r
(
W
−
1
(
K
L
K
+
μ
I
)
−
1
K
H
K
W
)
=max_{W} tr(W^{-1}(KLK+mu I)^{-1}KHKW)
=maxWtr(W−1(KLK+μI)−1KHKW)
此时可对
(
K
L
K
+
μ
I
)
−
1
K
H
K
(KLK+mu I)^{-1}KHK
(KLK+μI)−1KHK进行特征值分解,取最大的m个特征值对应的特征向量,组成W。
注1:目标是使映射后的数据方差最大化,为什么条件中直接把协方差矩阵固定为单位矩阵?之前我没搞明白,后来问了一下学长,得到了解决。
我们先假设这样一个问题,目标是最小化
W
T
A
W
W^{T}AW
WTAW,同时最大化
W
T
W
W^{T}W
WTW,那么我们可以把问题转化为最小化
W
T
A
W
W
T
W
frac{W^{T}AW}{W^{T}W}
WTWWTAW,可以看到W和kW在该式中结果是相同的,那么我们可以把问题转化为
m
i
n
W
W
T
A
W
min_{W}W^{T}AW
minWWTAW,s.t.
W
T
W
=
I
W^{T}W=I
WTW=I。
如果把上面问题中的
W
T
W
W^{T}W
WTW改为
W
T
B
W
W^{T}BW
WTBW,我们可以把B分解为
X
T
X
X^{T}X
XTX,令
W
~
=
X
W
widetilde{W}=XW
W
=XW,那么上面问题可以转化为最小化
(
X
−
1
W
~
)
T
A
X
−
1
W
~
(X^{-1}widetilde{W})^{T}AX^{-1}widetilde{W}
(X−1W
)TAX−1W
,同时最大化
(
W
~
)
T
W
~
(widetilde{W})^{T}widetilde{W}
(W
)TW
,那么仍然和上面一个思路。
我们回到TCA,令
A
=
K
L
K
+
μ
I
A=KLK+mu I
A=KLK+μI,
B
=
K
H
K
B=KHK
B=KHK,那么就可以按照上述思路进行理解。
其实LDA就是这个思想,当然上面的公式表示并不严谨,没有考虑矩阵是否可逆之类的,只是提供一个思路。
4 半监督TCA(SSTCA)
在上面的TCA中并没有用到源域的标签数据,另外在许多半监督学习算法中流形信息也是一个重要的组成部分,那么我们将这两点考虑到TCA中,就形成了半监督TCA(SSTCA)。
4.1 优化目标
SSTCA有三个目标:(1)在嵌入空间(就是上面提到的潜在低维空间)中将源域和目标域数据分布最大程度地对齐;(2)在嵌入空间中增强标签与数据的依赖关系;(3)保留数据的局部几何结构。
4.1.1 目标一:分布匹配
如无监督TCA中所述,最小化嵌入空间中源域数据和目标域数据之间的MMD距离。
4.1.2 目标二:标签依赖
HSIC可以衡量两个数据集的依赖关系,这里我们用于衡量嵌入空间中数据和标签的依赖关系,下面我们假设源域中全是已标注数据,目标域中全是未标注数据。
上面提到HSIC(X,Y)=
1
(
n
−
1
)
2
t
r
(
H
K
H
K
y
y
)
frac{1}{(n-1)^{2}}tr(HKHK_{yy})
(n−1)21tr(HKHKyy),其中H为中心化矩阵,在这个问题中K即为我们在经验核映射那一节的得到的
K
~
=
(
K
K
−
1
2
W
~
)
(
W
~
T
K
−
1
2
K
)
=
K
W
W
T
K
T
widetilde{K}=(KK^{-frac{1}{2}}widetilde{W})(widetilde{W}^{T}K^{-frac{1}{2}}K)=KWW^{T}K^{T}
K
=(KK−21W
)(W
TK−21K)=KWWTKT,现在我们构建
K
~
y
y
widetilde{K}_{yy}
K
yy,
K
~
y
y
=
γ
K
l
+
(
1
−
γ
)
K
v
widetilde{K}_{yy}=gamma K_{l}+(1-gamma )K_{v}
K
yy=γKl+(1−γ)Kv,其中
K
v
K_{v}
Kv是一个单位矩阵,对于
K
l
K_{l}
Kl,若
x
i
,
x
j
x_{i},x_{j}
xi,xj均属于源域,则
[
K
l
]
i
j
=
k
y
y
(
x
i
,
x
j
)
[K_{l}]_{ij}=k_{yy}(x_{i},x_{j})
[Kl]ij=kyy(xi,xj)(这里的
k
y
y
k_{yy}
kyy是标签数据的核函数),否则
[
K
l
]
i
j
=
0
[K_{l}]_{ij}=0
[Kl]ij=0。
将
K
~
widetilde{K}
K
和
K
~
y
y
widetilde{K}_{yy}
K
yy带入HSIC中得到优化目标,即最大化:
t
r
(
H
(
K
W
W
T
K
)
H
K
~
y
y
)
=
t
r
(
W
T
K
H
K
~
y
y
H
K
W
)
tr(H(KWW^{T}K)Hwidetilde{K}_{yy})=tr(W^{T}KHwidetilde{K}_{yy}HKW)
tr(H(KWWTK)HK
yy)=tr(WTKHK
yyHKW)
另外我们进行简单的推导:
t
r
(
H
(
K
W
W
T
K
)
H
K
~
y
y
)
tr(H(KWW^{T}K)Hwidetilde{K}_{yy})
tr(H(KWWTK)HK
yy)
=
t
r
(
H
(
K
W
W
T
K
)
H
(
γ
K
l
+
(
1
−
γ
)
K
v
)
)
tr(H(KWW^{T}K)H(gamma K_{l}+(1-gamma )K_{v}))
tr(H(KWWTK)H(γKl+(1−γ)Kv))
=
t
r
(
γ
H
(
K
W
W
T
K
)
H
K
l
+
(
1
−
γ
)
H
(
K
W
W
T
K
)
H
K
v
)
tr(gamma H(KWW^{T}K)HK_{l}+(1-gamma )H(KWW^{T}K)HK_{v})
tr(γH(KWWTK)HKl+(1−γ)H(KWWTK)HKv)
=
t
r
(
γ
H
(
K
W
W
T
K
)
H
K
l
+
(
1
−
γ
)
(
(
W
T
K
H
)
T
(
W
T
K
H
)
)
tr(gamma H(KWW^{T}K)HK_{l}+(1-gamma )((W^{T}KH)^{T}(W^{T}KH))
tr(γH(KWWTK)HKl+(1−γ)((WTKH)T(WTKH))
=
t
r
(
γ
H
(
K
W
W
T
K
)
H
K
l
+
(
1
−
γ
)
(
(
W
T
K
H
)
(
W
T
K
H
)
T
)
tr(gamma H(KWW^{T}K)HK_{l}+(1-gamma )((W^{T}KH)(W^{T}KH)^{T})
tr(γH(KWWTK)HKl+(1−γ)((WTKH)(WTKH)T)
可以看出前一项用于衡量映射后的数据和标签的依赖性,也就是说
K
~
y
y
widetilde{K}_{yy}
K
yy中的
K
l
K_{l}
Kl为HSIC中要求的
K
y
y
K_{yy}
Kyy即标签的核矩阵;第二项的则是映射后数据的方差,也就是TCA中的保留数据属性。可以看出这里定义的
K
~
y
y
widetilde{K}_{yy}
K
yy并不是HSIC最初要求的
K
y
y
{K}_{yy}
Kyy,而是进行了改进,引入了方差项。
γ
gamma
γ则是在建立映射后数据和标签依赖、映射后数据的方差两者之间进行权衡,当源域带标签数据较多时
γ
gamma
γ大一些(因为此时标签与数据的对应信息更多更准确),否则
γ
gamma
γ小一些。
4.1.3 目标三:局部信息保留
在MMDE中,通过对目标核矩阵增加距离限制来保留局部几何结构,例如对于样本
x
i
x_{i}
xi,获取K个最近邻的邻居
χ
k
chi _{k}
χk,对任意的
x
j
∈
χ
k
x_{j}in chi _{k}
xj∈χk,在源空间中两者的距离
d
i
j
=
∣
∣
x
i
−
x
j
∣
∣
d_{ij}=||x_{i}-x{j}||
dij=∣∣xi−xj∣∣,那么映射后也保持这个距离,我们进行平方就得到
∣
∣
ϕ
(
x
i
)
−
ϕ
(
x
j
)
∣
∣
2
=
K
i
i
+
K
j
j
−
2
K
i
j
=
d
i
j
2
||phi (x_{i})-phi (x_{j})||^{2}=K_{ii}+K_{jj}-2K_{ij}=d_{ij}^2
∣∣ϕ(xi)−ϕ(xj)∣∣2=Kii+Kjj−2Kij=dij2,每个满足要求的
x
i
,
x
j
x_{i},x{j}
xi,xj都有这样的限制,那么在上面MMDE的SDP问题中就会有很多约束条件。
为了避免这个问题,引入了亲密度矩阵M,若
x
i
x_{i}
xi和
x
j
x_{j}
xj为邻居,则
m
i
j
=
e
x
p
(
−
d
i
j
2
/
2
σ
2
)
m_{ij}=exp(-d_{ij}^{2}/2sigma ^{2})
mij=exp(−dij2/2σ2)(文中没说如果不是邻居时的定义,个人感觉可以定义为0),然后最小化
∑
m
i
j
∣
∣
[
W
T
K
]
i
−
[
W
T
K
]
j
∣
∣
2
sum m_{ij}||[W^{T}K]_{i}-[W^{T}K]_{j}||^2
∑mij∣∣[WTK]i−[WTK]j∣∣2,这么做并不是直接保持原空间中的距离,而是保持了原空间中的距离大小的相对关系,原空间中两个样本之间的距离越近,那么对应的
m
i
j
m_{ij}
mij越大,通过该目标函数,映射后两个样本之间的距离也就越近。
我们定义对角矩阵D,其中
d
i
i
=
∑
j
=
1
n
m
i
j
d_{ii}=sum_{j=1}^{n}m_{ij}
dii=∑j=1nmij,定义L’=D-M,那么上述问题可以转化为
m
i
n
W
t
r
(
W
T
K
L
′
K
W
)
min_{W}tr(W^{T}KL'KW)
minWtr(WTKL′KW)。
这部分的推导可以参照西瓜书301页,我在此进行了截屏:

4.2 目标函数
综合上面三个目标,我们最终的问题就要找到一个合适的矩阵W,目标函数如下:
m
i
n
W
t
r
(
W
T
K
L
K
W
)
+
μ
t
r
(
W
T
W
)
+
λ
t
r
(
W
T
K
L
′
K
W
)
min_{W}tr(W^{T}KLKW)+mu tr(W^{T}W)+lambda tr(W^{T}KL'KW)
minWtr(WTKLKW)+μtr(WTW)+λtr(WTKL′KW)
s.t.
W
T
K
H
K
~
y
y
H
K
W
=
I
W^{T}KHwidetilde{K}_{yy}HKW=I
WTKHK
yyHKW=I
对上面问题,我们可以仿照TCA解决的思路,将问题转化为
m
a
x
W
t
r
(
(
K
H
K
~
y
y
H
K
W
)
[
K
(
L
+
λ
L
′
)
K
W
+
μ
W
]
−
1
)
max_{W}tr((KHwidetilde{K}_{yy}HKW)[K(L+lambda L')KW+mu W]^{-1})
maxWtr((KHK
yyHKW)[K(L+λL′)KW+μW]−1),最终对
)
[
K
(
L
+
λ
L
′
)
K
+
μ
I
]
−
1
(
K
H
K
~
y
y
H
K
)
)[K(L+lambda L')K+mu I]^{-1}(KHwidetilde{K}_{yy}HK)
)[K(L+λL′)K+μI]−1(KHK
yyHK)进行特征值分解,取较大的m个特征值对应的特征向量组成矩阵W。
算法总结

最后
以上就是快乐饼干最近收集整理的关于迁移学习一——TCA和SSTCA1 背景2 知识准备3 无监督TCA4 半监督TCA(SSTCA)算法总结的全部内容,更多相关迁移学习一——TCA和SSTCA1内容请搜索靠谱客的其他文章。








发表评论 取消回复