我的学习笔记之概率、随机变量及其分布（R语言）

107 阅读 0 评论 71 点赞

我是靠谱客的博主幸福背包，最近开发中收集的这篇文章主要介绍我的学习笔记之概率、随机变量及其分布（R语言），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

要点
计算概率的方法；
离散型随机变量，二项分布、Poisson分布和超几何分布；
连续型随机变量，均匀分布、正态分布和指数分布；
抽样分布，卡方分布、t分布、F分布。

一、概率

1.多步骤试验（乘法法则）

1.模拟投掷两枚硬币的全部结果.

#expand.grid()函数计算多步骤函数的全部结果，格式：expand.grid(…,)
expand.grid(step1=c("H","T"),step2=c("H","T"))

#运行结果
step1 step2
1     H     H
2     T     H
3     H     T
4     T     T

2.某个项目被分割为两个阶段：阶段1是设计工作，阶段2是建设工作. 根据对以往的项目分析，完成设计工作可能需要2个月、3个月或4个月，完成建设阶段可能需要6个月、7个月或8个月. 试分析：完成整个项目共有多少中情况，每种情况各需多少个月？

#连乘计算函数prod(…, na.rm=FALSE)
#按照乘法法则，完成整个项目共有3×3=9种情况，使用expand.grid()函数计算具体情况和每种情况所花时间.
D<-expand.grid(sheji=c(2,3,4),shigong=c(6,7,8))
D$wanchengshijian<-apply(D,1,sum)  #求D每一行之和
D

#运行结果
 sheji shigong wanchengshijian
1     2       6               8
2     3       6               9
3     4       6              10
4     2       7               9
5     3       7              10
6     4       7              11
7     2       8              10
8     3       8              11
9     4       8              12

2.组合

第二种计数法则是组合法则，即同一时间从n个项目中抽取其中k个的组合数：

# 用choose(n,k)函数计算，如
 choose(5,3)
 #运行结果
[1] 10

3.从1～5个数中，随机取3个的全部组合.

# 函数combn(), 可生成全部组合方案，格式：combn(x,m,FUN=NULL,simplify=TRUE,…)
combn(1:5,3)
#运行结果
     [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,]    1    1    1    1    1    1    2    2    2     3
[2,]    2    2    2    3    3    4    3    3    4     4
[3,]    3    4    5    4    5    5    4    5    5     5
#如果要对全部组合情况做运算，如，求均值.
combn(1:5,3,FUN=mean)
#运行结果
[1] 2.000000 2.333333 2.666667 2.666667 3.000000 3.333333 3.000000 3.333333
[9] 3.666667 4.000000

4.从一副完全打乱的52张扑克中任取4张，计算下列事件的概率.
(1)抽取4张依次是红心A、方块A、黑桃A和梅花A的概率;
(2)抽取4张为红心A 、方块A、黑桃A和梅花A的概率.

(1)抽取4张是有顺序的，因此用排列求解. 所求事件的概率
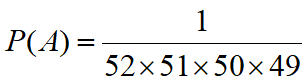
在这里插入图片描述

 1/prod(49:52)
 #运行结果
[1] 1.539077e-07

(2)抽取4张没有次序的，因此用组合来求解，
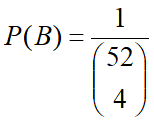
在这里插入图片描述

1/choose(52,4)
#运行结果
[1] 3.693785e-06

5.在例2中，完成项目的时间在8至12个月之间，计算恰好用8个月、9个月、…完成项目的概率.

#使用table()函数和prop.table()函数计算频数和相对频率.
D<-expand.grid(sheji=c(2,3,4),shigong=c(6,7,8))
D$wanchengshijian<-apply(D,1,sum)
D
Ta<-table(D$wanchengshijian)
prop.table(Ta)
#运行结果
 8         9        10        11        12 
0.1111111 0.2222222 0.3333333 0.2222222 0.1111111

二、离散型随机变量

6.假设100件产品中，有5件次品，现从中随机地抽取20件，求“次品数”的分布律.
解：设X为次品的随机变量，k为它的取值，
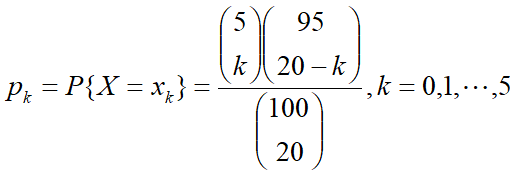
在这里插入图片描述

P<-numeric(6)
for(k in 0:5){
  P[k+1]<-choose(5,k)*choose(95,20-k)/choose(100,20)
}
P
#运行结果
[1] 0.3193094420 0.4201440026 0.2073437935 0.0478485677 0.0051482636 0.0002059305

7.计算例6中“次品数”的数学期望.

D<-expand.grid(sheji=c(2,3,4),shigong=c(6,7,8))
D$wanchengshijian<-apply(D,1,sum)
D
mu<-weighted.mean(x=0:5,w=P);mu

8.计算例6中“次品数”的方差.

D<-expand.grid(sheji=c(2,3,4),shigong=c(6,7,8))
D$wanchengshijian<-apply(D,1,sum)
D
mu<-weighted.mean(x=0:5,w=P)
weighted.mean((0:5-mu)^2,w=P)

1.二项分布

二项分布与二项试验有关，
(1)试验由一个包括n个相同试验的序列组成；
(2)每次试验有两种可能结果，一种称为成功，一种为失败；
(3)每次试验是相互独立的；
(4)每次试验成功的概率相同，均为p.

设X表示二项试验中成功的次数，{X=k}表示事件：n次试验中恰好有k次成功，则
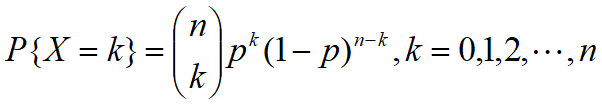
在这里插入图片描述
分布函数为

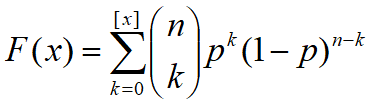
二项分布的期望与方差为：
E(x) = np Var(x)=np(1-p)

在R中binom表示二项分布,
dbinom表示概率密度
pbinom表示分位数
函数的使用格式为：
dbinom(x,size,prob,log=FALSE)
pbinom(q,size,prob,lower.tail=TRUE,log.p=FALSE)
qbinom(p,size,prob,lower.tail=TRUE,log.p=FALSE)

9.现有80台同类型的设备，各台设备的工作是相互独立的，发生故障的概率是0.01，且一台设备的故障能由一人处理. 配备维修工人的方法有两种，一种是4人分开维护，每人负责20台，另一种是由3人共同维护80台. 试比较两种方法在设备放生故障时不能及时维修的概率的大小.
解：设X为同一时刻发生故障的台数. 第一种情况是计算概率P(X≥2),第二种情况是计算概率P(X≥4).

p1<-1-pbinom(1,size=20,prob=0.01);p1
[1] 0.01685934
p2<-1-pbinom(3,size=80,prob=0.01);p2
[1] 0.008659189

10.为保证设备的正常运行，必须配备一定数量的设备维修人员. 现有同类设备180台，且各台工作相互独立，每台设备任一时刻发生故障的概率都是0.01. 假设一台设备的故障由一人进行维修，问至少配备多少名维修人员，才能保证设备发生故障后能得到及时修理的概率不小于0.95?
解：设随机变量X为发生故障的设备数，k为配备修理工的个数，由题意X~B(n,p), 其中n=180, p=0.01, 且满足P(x≥k)≥0.95

n<-180;p<-0.01;k<-qbinom(.95,n,p);k  #分位数
#运行结果
4

2.Poisson分布

如果事件满足：
(1)事件在任意两个等长度的区间内放生一次的概率相等；
(2)事件在任意区间内是否发生与其他地区发生情况相互独立.
则事件发生次数就是用Poisson分布来描述的随机变量.
分布律（事件在一个区间内发生k次的概率）：
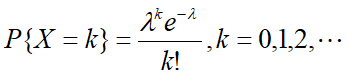
在这里插入图片描述
分布函数：

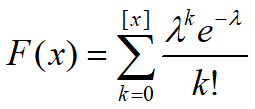
Poisson分布的期望和方差均为λ.
Poisson分布常用来描述不经常发生的事件，也称为“不经常事件定律”. 例如，某化工厂发生严重事故的概率很小，可用Poisson分布来描述.
Poisson分布还经常用来描述某时间段的到达数，如果某段时间的到达数目太大，可缩短时间，使这个时间段内的时间发生的数目减少. 例如，可以考虑在5分钟内到达某花店的人数.

R中，pois表示Poisson分布，概率密度函数、分布函数、分位数分别为：
dpois(x,lambda,log=FALSE)
ppois(q,lambda,lower.tail=TRUE,log.p=F)
qpois(p,lambda,lower.tail=TRUE,log.p=F)

11.假定顾客到达某银行的平均值是每4分钟3.2名，计算:
(1)在4分钟内有7名以上顾客的概率；
(2)在8分钟内到达10名顾客的概率.
解：（1）设X为4分钟内到达银行的顾客数，题意是计算P{X>7}，即计算1-P{X≤7}.

1-ppois(7,lambda=3.2)  
[1] 0.01682984

从结果看，在4分钟内不大可能有7名以上顾客到达银行.
（2）调整参数lambda=6.4. (不能将问题改为4分钟内到达5名顾客的概率.)

dpois(10,lambda=3.2*2)
[1] 0.05279004

12.计算机硬件公司制作某种型号芯片，其次品率为0.1%，各芯片成为次品相互独立. 求1000只芯片中至少有2只次品的概率.
解：设X为次品个数，计算概率P(X≥2). 现选择两种计算方法，先用二项分布精确计算，再用Poisson分布近似计算.

> 1-pbinom(1,size=1000,prob=0.001)
[1] 0.2642411
> 1-ppois(1,lambda=1000*0.001)
[1] 0.2642411

3.超几何分布

令r表示容量为N的总体中表示成功的元素个数. 令N-r为失败的个数. 超几何分布考虑在n次无放回的实验中，成功k次失败n-k次的概率.
分布律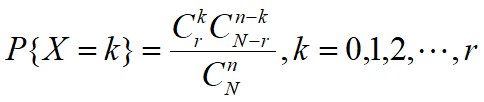：在这里插入图片描述
P(X=k)表示n次试验中获得k次成功的概率, n表示试验次数, N表示总体元素个数, r表示总体内成功的元素个数.
分布函数：

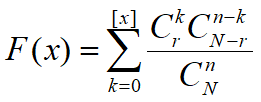
期望：

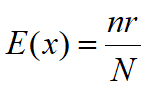
R中，hyper表示超几何分布，
概率密度 dhyper(x,m,n,k,log=FALSE)
分布函数phyper(q,m,n,k,lower.tail=TRUE,log=FALSE)
分位数qhyper(p,m,n,k, lower.tail=TRUE,log=FALSE)
x或q表示总体中试验成功的次数（k）, m表示成功次数（r）,n表示失败总次数（N-r）, k表示试验次数（n）

13.假设在10位喜欢喝可乐的人中，有6位喜欢可口可乐，4位喜欢百事可乐. 现从10人中任取3人，计算:
(1)3人中恰有2人喜欢可口可乐的概率;
(2) 3人中多数人（2人或3人）喜欢百事可乐的概率.
解：超几何分布. 设喜欢可口可乐为成功,喜欢百事可乐为失败, 成功的总次数为6, 失败的总次数为4, 试验总次数为3.
问题1是计算恰好2次成功的概率; 问题2是计算成功的次数小于1的概率.

dhyper(x=2,m=6,n=4,k=3)
[1] 0.5
> phyper(q=1,m=6,n=4,k=3)
[1] 0.3333333

事实上，例6中的“次品数”就服从超几何分布，因此计算分布律：

dhyper(x=0:5,m=5,n=95,k=20)
[1] 0.3193094420 0.4201440026 0.2073437935 0.0478485677 0.0051482636 0.0002059305

三、连续型随机变量

密度函数：非负函数f(x)
分布函数：
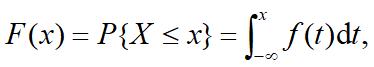
在这里插入图片描述
数学期望：

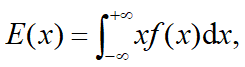
方差：

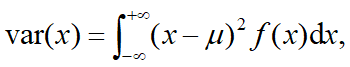
1.均匀分布 X~U(a,b)

密度函数：
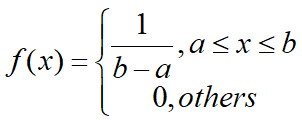
在这里插入图片描述
分布函数：

数学期望：

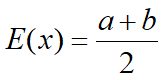
方差：

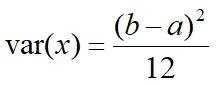
R中，unif表示均匀分布，
密度函数dunif(x,min=0,max=1,log=F)
分布函数punif(q,min=0,max=1,lower.tail=TRUE,log.p=FALSE)
分位数qunif(p,min=0,max=1,lower.tail=TRUE, log.p=FALSE)
x或q为密度或分布函数的自变量，p为分为点的概率，min、max为区间的端点
14.某设备生产出的钢板厚度在150mm至200mm之间，且服从均匀分布，钢板厚度在160mm以下为次品，求次品的概率.

p<-punif(160,min=150,max=200);p
[1] 0.2

2.正态分布

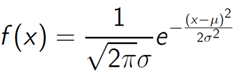
在这里插入图片描述

R中函数：
密度函数 dnorm(x,mean=0,sd=1,log=F)
分布函数pnorm(x,mean=0,sd=1,lower.tail=TRUE,log.p=F)
分位数qnorm(p,mean=0,sd=1,lower.tail=TRUE, log.p=FALSE)

设 X服从正态分布，分别计算
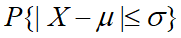
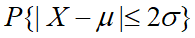
在这里插入图片描述

和

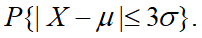
p<-pnorm(x)-pnorm(-x);p
[1] 0.6826895 0.9544997 0.9973002

15.某项研究表明：居住在城市的居民每天平均产生1.6kg的生活垃圾。假定居民每天产生垃圾的数量X服从正态分布，标准差为0.47kg, 试计算67.72%的居民产生的生活垃圾大于多少kg.
解：
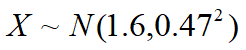
在这里插入图片描述
求在0.6772处的上分位数，有两种方法：

> qnorm(1-0.6772,mean=1.6,sd=0.47)
[1] 1.383855
> qnorm(0.6772,mean=1.6,sd=0.47,lower.tail = F)
[1] 1.383855
#lower.tail=F表示上侧分位数， lower.tail=T表示下侧分位数.

二项分布的正态近似
二项分布是离散型的，当n较大时，有时会计算困难，常常使用正态分布近似二项分布. 设n为试验次数，p为试验成功的概率，当n和p满足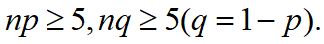：在这里插入图片描述
二项分布的随机变量X近似服从正态分布，即

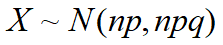
16. 设X~B(n,p)，且n=10,p=0.5
(1)试用二项分布精确计算P(X<=4)；
(2)试用正态分布近似计算P(X<=4).

> n<-10; p<-0.5; q<-1-p
> p1<-pbinom(4,size=n,prob=p);p1
[1] 0.3769531
> p2<-pnorm(4,mean=n*p,sd=sqrt(n*p*q));p2
[1] 0.2635446

P1=0.3769531, p2=0.2635446, 两者相差挺大。为什么？
从离散分布到连续分布，需要根据情况增加或减少0.5的修正，即连续性修正. 经过修正后，基本能保证二项分布的绝大部分信息正确地转换成正态分布的信息.

p3<-pnorm(4.5,mean=n*p,sd=sqrt(n*p*q));p3
[1] 0.3759148

可见修正后p3=0.3759148, 与二项分布的p1相差不大.

3.指数分布

描述完成任务所花时间非常有用，比如描述车辆到达修理厂的时间间隔，装运一辆卡车所需的时间等.
密度函数：
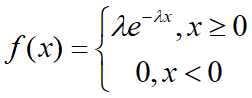
在这里插入图片描述
分布函数：

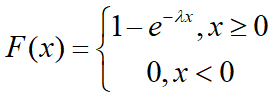
数学期望和方差：

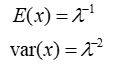
指数分布与Poisson分布的关系：
Poisson分布是确定在一特定的时间段内事件发生的次数. 而指数分布则是描述两个事件的间隔长度. 例如，假设在1小时内到达洗车店的汽车服从Poisson分布，其均值为每小时10辆汽车，则车辆的间隔时间服从指数分布，且平均间隔为1/10小时.

R中，exp表示指数分布，
密度函数 dexp(x,rate=1,log=F)
分布函数 pexp(q,rate=1,lower.tail=T,log.p=F)
分位数 qexp(p,rate=1,lower.tail=T,log.p=F)
参数rate为指数分布的参数 λ，默认值为1

17.英格兰在1875-1951年期间，矿山发生导致不少于10人死亡的事故的频繁程度，得知相继两次事故之间的时间T(天数)服从指数分布，其平均值为241天，求概率P(50≤T≤100).

> p<-pexp(c(50,100),rate=1/241)
> p[2]-p[1]
[1] 0.1522571

四、抽样分布

统计量是样本的函数, 也是随机变量, 统计量的概率分布称为抽样分布.

1. 简单随机抽样

如果每一个可能的样本被抽到的可能性相等.
样本不放回和有放回抽样.
在R中，用sample()函数模拟抽样，格式：
sample(x,size,replace=FALSE,prob=NULL)

18.（1）从1～10个数中随机地抽取3个。

sample (1:10,3)   
[1] 8 2 7 
#或者  
sample(10,3)
[1] 10  7  6

（2）做10次抛硬币的试验：

sample(c("H","T"),10,replace=TRUE)
 [1] "T" "H" "H" "H" "H" "H" "H" "T" "H" "T"

（3）模拟n重伯努力试验：

sample(c("S","F"),10, replace=TRUE,prob=c(0.7,0.3))

2. 常用统计量

样本均值：
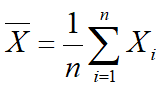
在这里插入图片描述
样本方差：

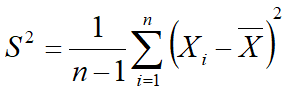
3.卡方分布

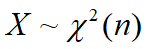
在这里插入图片描述
若Z_i ~N(0,1) (i=1,2,…,n)，且相互独立，则称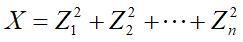为自由度为n的卡方分布，E(x)=n,var(X)=2n.

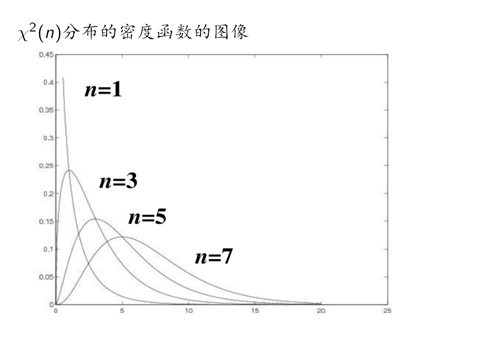
R中，chisq表示分布，
密度函数：dchisq(x,df,ncp=0,log=FALSE)
分布函数: pchisq(q,df,ncp=0,lower.tail=TRUE,log.p=FALSE)
分位数：qchisq(p,df,ncp=0,lower.tail=TRUE,log.p=FALSE)
df为自由度，ncp为非中心化参数，默认值为0

4.T分布

若随机变量Z~N(0,1),X服从自由度为n的卡方分布，且Z与X相互独立.则称
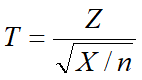
在这里插入图片描述
为自由度为n的t分布，

密度函数：dt(x,df,ncp=0,log=FALSE)
分布函数：pt(x,df,ncp=0,lower.tail=TRUE,log=FALSE)
分位数： qt(p,df,ncp=0,lower.tail=TRUE,log=FALSE)
df为自由度，ncp为非中心化参数，默认值为0

5.F分布

若随机变量X服从自由度为n₁的卡方分布，Y服从自由度为n₂的卡方分布，且相互独立.则称
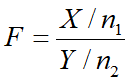
在这里插入图片描述
为自由度为(n₁,n₂)的F分布.

密度函数：df(x,df1, df2,ncp=0,log=FALSE)
分布函数： pf(q,df1,df2,ncp=0,lower.tail=TRUE,log=FALSE)
分位数： qf(p,df1,df2,ncp=0,lower.tail=TRUE,log=FALSE)
df1为第1自由度， df2为第2自由度.

6.统计量的分布

1.单个正态总体样本均值与方差的分布
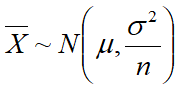
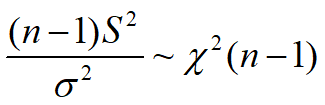
在这里插入图片描述

且相互独立。
由t分布的性质，得到：

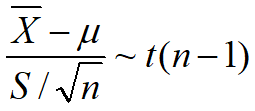
19.在总体N(80,20²)中随机抽取一个容量为100的样本，求样本均值与总体均值差的绝对值大于3的概率.

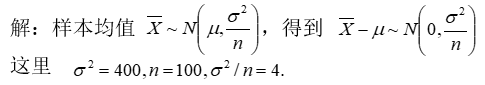
p<-1-pnorm(3,0,2)+pnorm(-3,0,2);p
[1] 0.1336144

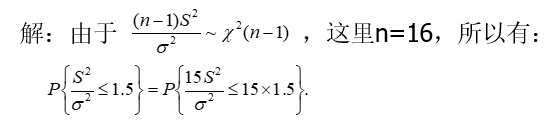
在这里插入图片描述

p<-pchisq(q=15*1.5,df=15);p
[1] 0.9046518

21.某台仪器测量的数据存放在measure.data中，设数据的总体服从正态分布，μ为总体均值，计算
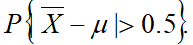
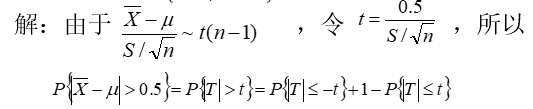
在这里插入图片描述

> X<-scan("measure.data")
Read 29 items
> n<-length(X);S<-sd(X);t<-0.5/(S/sqrt(n))
> pt(-t,df=n-1)+1-pt(t,df=n-1)
[1] 0.05615046

在这里插入图片描述

最后

以上就是幸福背包为你收集整理的我的学习笔记之概率、随机变量及其分布（R语言）的全部内容，希望文章能够帮你解决我的学习笔记之概率、随机变量及其分布（R语言）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：r语言
浏览次数：107 次浏览
发布日期：2023-05-16 01:37:01
本文链接：https://www.kaopuke.com/article/k-p-k_14_ujo_2_f2_12__7_kz.html

我的学习笔记之概率、随机变量及其分布（R语言）

概述

一、概率

1.多步骤试验（乘法法则）

2.组合

二、离散型随机变量

1.二项分布

2.Poisson分布

3.超几何分布

三、连续型随机变量

1.均匀分布 X~U(a,b)

2.正态分布

3.指数分布

四、抽样分布

1. 简单随机抽样

2. 常用统计量

3.卡方分布

4.T分布

5.F分布

6.统计量的分布

最后

评论列表共有 0 条评论

发表评论取消回复

我的学习笔记之概率、随机变量及其分布（R语言）

概述

一、概率

1.多步骤试验（乘法法则）

2.组合

二、离散型随机变量

1.二项分布

2.Poisson分布

3.超几何分布

三、连续型随机变量

1.均匀分布 X~U(a,b)

2.正态分布

3.指数分布

四、抽样分布

1. 简单随机抽样

2. 常用统计量

3.卡方分布

4.T分布

5.F分布

6.统计量的分布

最后

相关文章

评论列表共有 0 条评论

发表评论 取消回复

发表评论取消回复