差分电路的噪声分析

86 阅读 0 评论 57 点赞

我是靠谱客的博主眼睛大衬衫，最近开发中收集的这篇文章主要介绍差分电路的噪声分析，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

之前一直对差分电路的噪声分析存在恐惧，特来整理一波。

求下图差分电路中三个mos管对差模输出的热噪声 $overline{dV_{out}^2}$ ，且假设mos管的 $λ = γ = 0$ 。

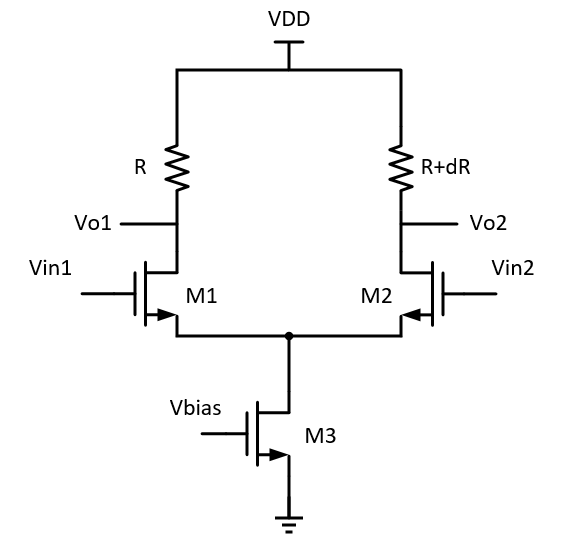
由于两个输入端的噪声不相关，因此不能用源极虚地的方式求输入到输出的增益（虽然最后结果确实一样）。

1、M1、2对输出噪声

先考虑M1管的热噪声，其噪声等效到栅极为：
$overline{dV_{n1}^2}=frac{4kT gamma}{g_{m1}}$
下面用小信号模型计算该输入对两个差模输出的增益：
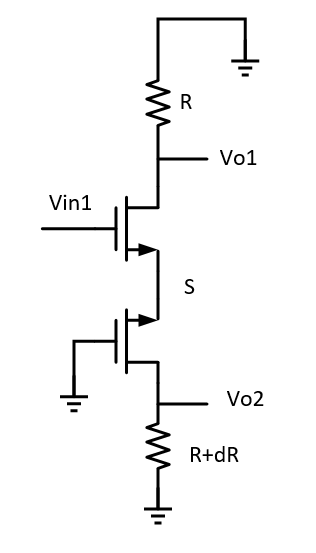
等效电路图
列KCL方程可得：
$frac{V_{o1}}{R}+(V_{in1}-V_s)g_{m1}=0 \ (V_{in1}-V_s)g_{m1}= V_s g_{m2} \ frac{V_{o2}}{R}=V_s g_{m2} end{cases}$
由 $g_{m1}=g_{m2}=g_m$ 解得：
$V_{o1}=-frac{g_mR}{2} V_{in1}\ V_{o2}= frac{g_mR}{2} V_{in1}$
因此M1对输出的噪声贡献：
$overline{dV_{oM1}^2}=frac{4kT gamma}{g_{m1}}(g_mR)^2=4kT gamma g_{m}R^2$

由对称性可以知道，M2对输出的噪声也是：
$overline{dV_{oM2}^2}=4kT gamma g_{m}R^2$

2、M3对输出噪声

M3为尾电流管，在电路对称的情况下，其对输出的增益为0，也就是说两边的噪声是相关的，会互相抵消，但是电路的负载电阻存在失配，因此会产生小的增益变化：
$A_3=frac{V_{o2}-V_{o1}}{V_3}=frac{V_3g_{m3}frac{1}{2}Delta R}{V_3}=frac{1}{2}g_{m3}Delta R$
所以M3对输出的噪声贡献：
$overline{dV_{oM3}^2}=frac{4kT gamma}{g_{m3}}(frac{1}{2}g_{m3}Delta R)^2=kT gamma g_{m3}Delta R^2$