定点数和浮点数_Simulink模型中定点数的介绍

本文摘要：

主要介绍Simulink模型中的定点数的概念，使用注意点，以及定点数与浮点数之间的数据转换。

定点数与浮点数的概念

当我们给Simulink的模块输出设置数据类型时，可以看到有如下的选项：

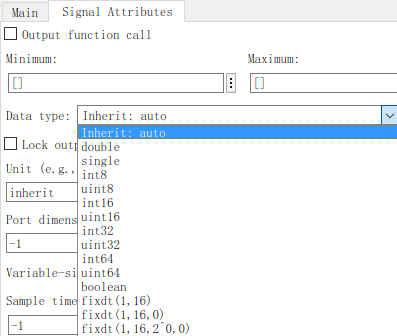
这里，除了double和single是表示浮点数数据类型，其他剩下的都可以称为定点数数据类型。

对于浮点数和定点数，也可以从计算机存储数值与现实想表示的数值两者之间的关系来理解：

• 对于浮点数，可以理解为，计算机存储的数据值和实际现实中想表示的数据值是一样的。

• 对于定点数，可以理解为，计算机存储的数据值和实际现实中想表示的数据值有一个固定的转换关系。

浮点数介绍

single表示单精度浮点类型，数据长度为32位，其中第一位是符号位s，0表示正数，1表示负数。接下来的8位是指数E，剩下的32位是有效数字 M

在IEEE754标准中，一个规格化的32位浮点数x的真值表示为：

x = (-1)^s * (1.M) * 2^(E-127)

比如如图所示，s=0，M=01，E=124，则表示的数为：

(-1)^0 * (1.01) * 2^(124-127) = (1.25)^(-3) = 0.15625

单精度浮点数可以表示的有效数字的位数大概为2^23这个数量级，即7-8位有效数字。

double表示双精度浮点类型，数据长度为64位，其中符号位s的长度为1位，指数E的长度为11位，有效数字M的长度为52位。可以表示的有效数字大概为16位。

可以见对于浮点数数据类型，计算机的表示方法是根据数值的大小自动按照规定的格式存储的，我们不需要在意其小数点的位置，因为这个是浮动的，浮点数的名字也因此而得名。并且按照规定在计算机内表示的值和实际中的值是一样的。

定点数介绍

接下来的int8，uint8，int16，uint16，int32，uint32，int64，uint64，boolean，可以归结为一类：无小数点的固定点数。

对于这一类型的数据，由于没有小数点，所以计算机存储的数据值和实际现实中想表示的数据值也是相等的，也就是转化关系固定为相等。

fixdt(1,16)，也属于无小数点的固定点数，其中第一位表示符号位，0表示无符号，1表示有符号，第二位表示数据的长度。比如fixdt(1,16)就相当于int16；fixdt(0,32)就相当于uint32。

fixdt(1,16,0)表示小数点就是在2进制数据的某一位。

比如下图所示，有一个16位无符号的二进制数，小数点在从右往左数的第四位，则该类型可以定义为fixdt(0,16,4)

对于fixdt(0,16,4)这类型的数据，假设计算机存储的值是0xFFFF，那实际现实中想表示的值为 65535 * 2^(-4) = 4095.9375

当然，小数点还可能不在二进制数内的某一位，而是在这个位数之外，比如对于fixdt(0,16,-4)类型的数据，假设计算机存储的值是0x0001，那实际现实中想表示的值为 1 * 2^(4) = 16。

这种类型可以表示任何小数点在二进制数据中任何一位的情况，但如果小数点不刚好在二进制数中的某一位，那就要用下下面的格式来定义定点数类型了

fixdt(1,16,2^0,0)的适用范围就更广泛了。其中第一个参数仍然是符号位，第二个参数是数据长度，第三个参数是分辨率，第四个参数是偏移量。这样，就可以表示任意的计算机内存储数值到实际数值的线性转化。

比如现实中我们温度的范围是-40摄氏度到200摄氏度，我们想把温度数值在计算机内用一个16位无符号的数来存储。假设这个存储的数据类型为fixdt(0,16,0.01,-40)。

那么假设计算机存储的值是0x0001，那实际现实中想表示的值为 1 * 0.01 -40 = -39.99。假设计算机存储的值是0x0FFF，那实际现实中想表示的值为 4095 * 0.01 -40 = 0.95。

也就是说，计算机内部存储值与现实实际值之间的转换关系为：

实际值 = 计算机内部值 * 分辨率 + 偏移量

定点数据类型在Can通信中的应用

由于DBC中，定义一个信号经常会用到分辨率和偏移量的概念，这个和Simulink中定点数的概念是一样的，所以如果我们想要方便的接收和发送Can信号，就可以使用定点数据类型。

比如我们想要接收两个can信号，车速(DBC中定义的分辨率为0.01，偏移量为0)和电池温度(DBC中定义的分辨率为0.01，偏移量为-40)。发送一个can信号，扭矩(DBC中定义的分辨率为0.1，偏移量为0)。那么我们只要将接口端口的数据类型设置为对应的定点数据类型，然后接收的时候添加 DataTypeConversion模块，将数据类型转化为计算比较方便的浮点类型，就可以用于后续的计算了。发送的时候，如果计算时采用浮点数，那也只要添加DataTypeConversion模块，将数据类型转化为发送变量对应的定点数据类型，就可以按照DBC中定义的格式发送了。

示意模型如下：

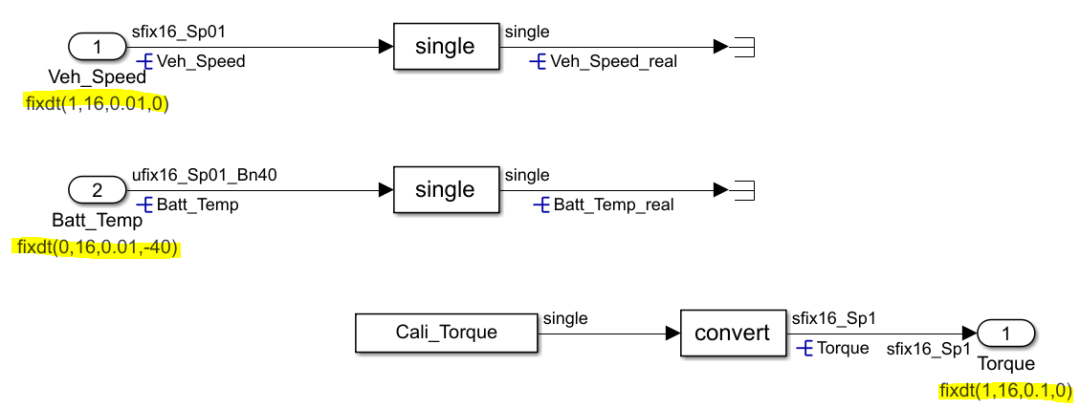
这个模型生成的代码如下：

可以看到，通过设置对应的定点数据类型和添加数据转换模块，在生成代码时，就会自动添加DBC中定义的分辨率和偏移量转换的代码，省去了自己搭模型转化的过程。

定点数四则运算的规范

相比于浮点数，定点数的四则运算要麻烦很多，有不少要注意的地方。

1. 对于加减法一定要保证两个变量的分辨率和偏移量一样，如果不一样，要将低分辨率的转为高分辨率的定点数之后，再进行加减计算。

2. 对于乘法和除法，不推荐偏移量不为0的定点数变量进行的乘法运算。因为带有偏移量之后，乘除法的运算就比较难以理解了。

3. 对于乘法，两个偏移量均为0，分辨率分别为r1和r2的定点数相乘后，新的分辨率为两个变量分辨率相乘。即r = r1*r2。

4. 对于除法，两个偏移量均为0，分辨率分别为r1和r2的定点数相除后，新的分辨率为两个变量分辨率相除。即r = r1/r2。这里要注意的是，如果希望相处后的变量的分辨率仍然为r1，那么需要在相除前，把变量1的分辨率提高到r1*r2，然后再进行除法运算，这样结果的分辨率才是r1。

5. 所有运算都要考虑两个变量数据范围，保证在进行计算之后，不会发生溢出。比如，两个数的数据类型都是fixdt(0,16,0.01,0)，实际值范围都是0~350，那么对应的计算机值的范围就是0~35000，那么相加后的范围就是0~70000，70000已经超过了16位无符号数的最大值65535，所以这两个变量相加后，数据类型要设为fixdt(0,32,0.01,0)，否则就有溢出的可能。但如果两个数的实际值范围都是0~300，那么相加后的数据类型就还可以继续设为fixdt(0,16,0.01,0)。

定点数和浮点数的精度

定点数由于小数点是固定的，所以精度也是固定的，所以定点数可以进行精确的比较，误差也是明确在一个精度之类的。

浮点数由于小数点是根据数值的范围变化的，所以精度是不固定的，所以两个浮点数是很难刚好相等的。所以是禁止两个浮点数进行等于比较的。

对于单精度浮点数，有效数据是7位，也就是说，他可以比较精确的表示 0.0000001和1000000，但是如果是1000000 + 0.0000001，那就没办法精确表示了。

比如我们看如下的模型，从250000开始，每次加0.01，数据类型分别为单精度浮点型和分辨为0.01的32位无符号定点类型

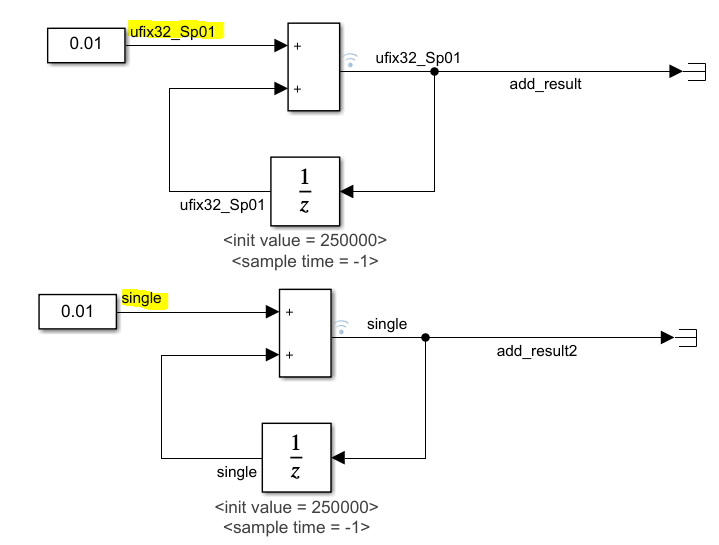
仿真结果如下，对于单精度浮点型，发现累加到262114之后，就不会再累加了，因为那时浮点数的精度已经无法支持加0.01了，所以加了也相当于没加。

对于定点类型，累加的结果一直都是精确的。

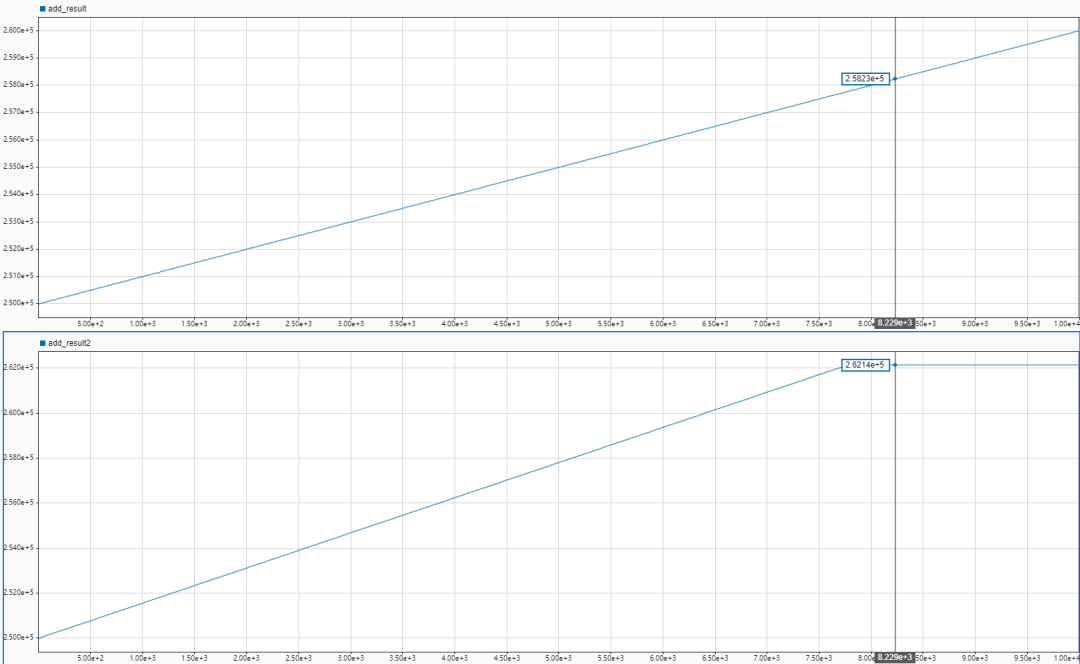
所以，也不是任何情况都使用单精度浮点类型是最优的情况。对于大范围的累加，定点数有着更好的表现。