【数字逻辑与EDA技术】数字电子技术基础-期末考试重点总结第一章数制和码制第二章、逻辑代数基础第三章门电路第四章组合逻辑电路第五章半导体存储电路第六章时序逻辑电路第七章有限状态机

59 阅读 0 评论 39 点赞

我是靠谱客的博主传统招牌，最近开发中收集的这篇文章主要介绍【数字逻辑与EDA技术】数字电子技术基础-期末考试重点总结第一章数制和码制第二章、逻辑代数基础第三章门电路第四章组合逻辑电路第五章半导体存储电路第六章时序逻辑电路第七章有限状态机，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

啊，6月就要期末考试了耶，那就浅浅地复习一下下叭

第一章数制和码制

一、四种进制之间的进制转换

二进制 B

八进制 O

十进制 D

十六进制 H

巧记：BODH 谐音：拨(BO)电(D)话(H)

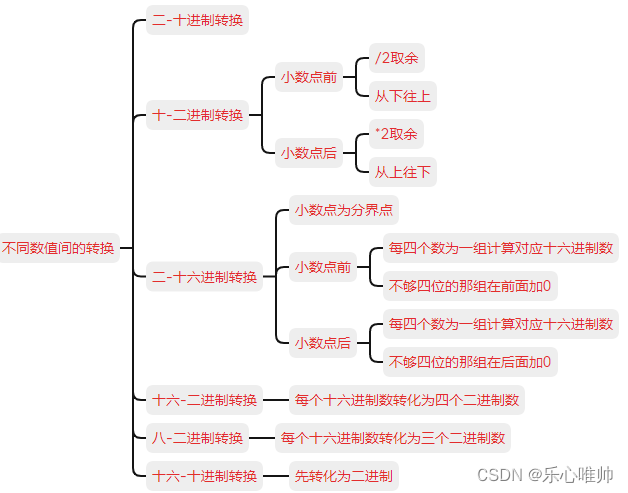
二、浮点数的进制转换

十-二转换

小数点前面的数除以二，小数点后面的数乘以二。

例： $(173.8125)_{10}=(10101101.1101)_{2}$

二-十转换

小数点往前的数依次乘以2的零次方、一次方、二次方；小数点往后的数依次乘以2的负一次方、负二次方、负三次方......

例： $(1011.01)_{2}$

三、反码、补码和补码运算

反码的求法

正数反码与原码相同，负数如果有符号位，则符号位不变，其余每个二进制位取反，即0变成1、1变成0。

补码的求法

正数补码与原码相同，负数如果有符号位，则符号位不变，其余位各位取反后，再加1；若无符号位，则直接各位取反后，再加1。

补码运算

一般是同一进制数之间的加减法

如果两个数同号，则先计算两个数的绝对值，判断出需要m个有效二进制数表示数的大小，然后再加一个符号位，也就是一共有m+1个二进制数来表示此次运算过程。

例：1101+0101，-1011-1010.

如果两个数异号，和的绝对值一定小于其中的绝对值比较大的那个绝对值，所以补码的数值部分不需要增加位数。

例：1110-0111，0111-1110.

负数的补码求原码

将此补码再求补，得到的就是原码。

四、常见的编码方式（了解即可）

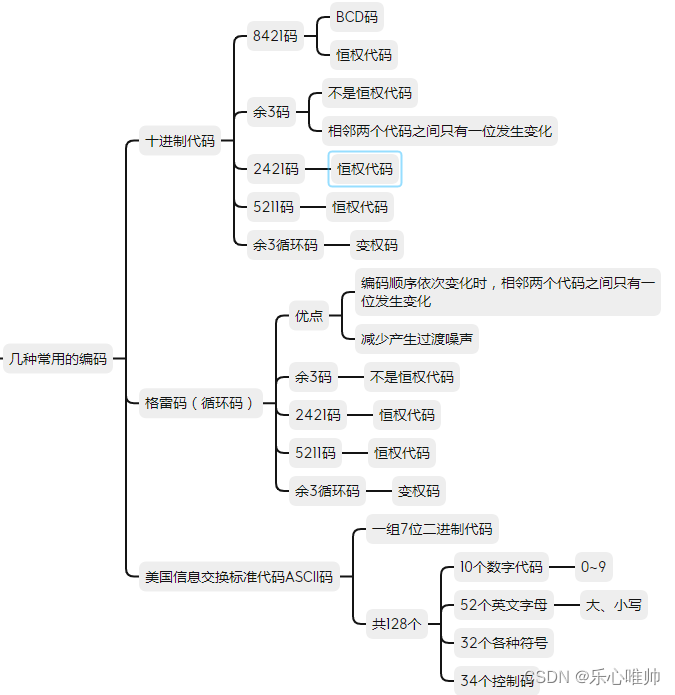
十进制代码

8421码，又称BCD码

格雷码，又称循环码

ASCII码一组7位二进制码，共128个。

第二章、逻辑代数基础

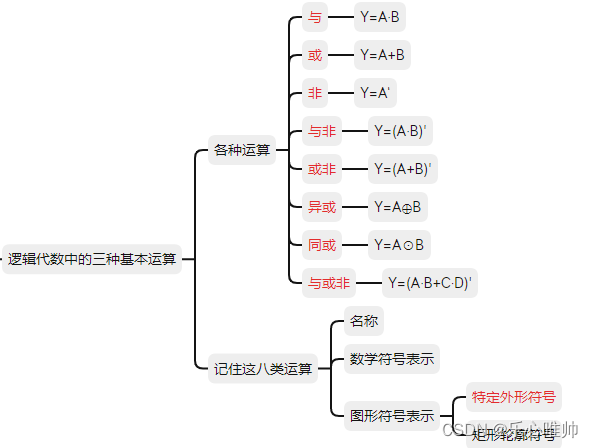
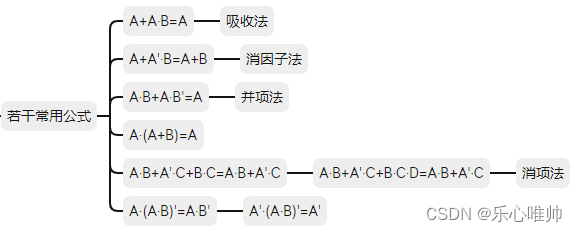
一、逻辑等式的证明

方法一：逻辑式的真值表是否相同，若相同，则等式成立。

方法二：逻辑代数的公式和定理将等式两边化成完全相同的形式，则等式成立。

方法三：分别画出等式两边逻辑式的卡诺图，若卡诺图相同，则等式成立。

二、逻辑函数不同描述方法之间的转换

真值表→逻辑式

逻辑式→逻辑图

逻辑式→卡诺图

波形图→真值表

逻辑式→真值表

逻辑图→逻辑式

其他的互相转换：利用上边的几种基本的转换方法，可以实现任意两种表示方法之间的转换。

三、逻辑函数式的变换

1、与或形式→与非-与非形式

方法：利用摩根定理将整个与或式两次求反

2、与或形式→与或非形式

方法：先画出卡诺图，将填入0的那些最小项合并、再求反。

3、与或形式→或与形式

方法一：先转化为与或非形式，然后用摩根定理。

方法二：反复运用公式A+BC=（A+B）（A+C）进行运算

4、与或形式→或非-或非形式

方法：先转化为与或非形式，再用摩根定理将与或非中的每个乘积项化为或非的形式。

5、将逻辑函数式化为最小项之和的形式

方法：先利用逻辑代数的公式和定理将函数式转化成与或形式，在利用乘（A+A'）补齐缺项

四、逻辑函数的化简

公式化简法

卡诺图化简法

多输出逻辑函数的化简（了解）

第三章门电路

二极管、三极管、CMOS反相器的识别（了解）

第四章组合逻辑电路

一、数据选择器的应用（了解）

二、译码器的应用（了解）

三、加法器的应用（了解）

四、数值比较器的应用（了解）

五、编码器的应用（了解）

ps：表示反相的小圆圈在逻辑图形符号的输入端，是为了强调说明“低电平有效”。

习题类型

一、组合逻辑电路分析

分析给定逻辑电路（可能是小规模集成门电路组成，也可能是中规模集成常用组合逻辑电路组成）的功能，写出它的逻辑函数式或功能表，来让逻辑功能更加直观、明了。

二、组合逻辑电路设计

用小规模集成门电路设计组合逻辑电路

进行逻辑抽象，把要求实现的逻辑功能表述为一个逻辑函数形式。
1. 确定输入变量和输出变量。
2. 定义逻辑状态的含义。
3. 列出真值表。
写出逻辑函数式。可通过真值表写出，也可直接写出。
将逻辑函数式化简或者变换。所含乘机项最少，同时每个乘机项的因子最少。
画出逻辑电路图。

用数据选择器设计组合逻辑电路

用译码器设计组合逻辑电路

用加法器设计组合逻辑电路

用Verilog HDL语言描述一个逻辑电路模块

根据Verilog HDL语言的描述画出相应的逻辑电路图

作业：4.1、4.6、4.9、4.21、4.22

第五章半导体存储电路

一、触发器的种类

SR触发器、JK触发器、D触发器、T触发器

四种触发器真值表及其功能
T	D	JK		SR		SR
T	D	J	K	S	R	S'	R'	Q	Q*
0（保持）	无	0	0	0	0	1	1	保持	保持
无	1	1	0	1	0	0	1	X	1
无	0	0	1	0	1	1	0	X	0
1（翻转）	无	1	1	1	1	0	0	X	特殊
Q*=TQ'+T'Q	Q*=D	Q*=JQ'+K'Q		Q*=S+R'Q		Q*=S+R'Q

特殊情况解释：

SR不允许输入（1，1）；
JK的（1,1）是翻转；
T的（1,1）是翻转；
D无法进入这种情况。

二、触发方式

电平触发、边沿触发、脉冲触发

1、电平触发

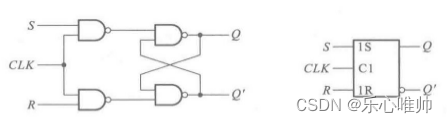
clk输入端没有小圆圈时，表示clk高电平为有效信号。

假设没有小圆圈，在clk=1的全部时间里，输入信号的变化都会引起输出状态的变化。

假设有小圆圈，那就是在clk=0的全部时间里，输入信号的变化都会引起输出状态的变化。

2、边沿触发

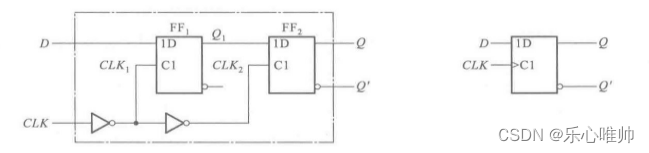
特点是有主从结构。

clk输入端没有小圆圈时，触发器的次态仅仅取决于clk上升沿到达前瞬间输入端的状态，而与此前和此后输入信号的状态无关。

clk输入端没有小圆圈时，触发器的次态仅仅取决于clk下降沿到达前瞬间输入端的状态，而与此前和此后输入信号的状态无关。

3、脉冲触发

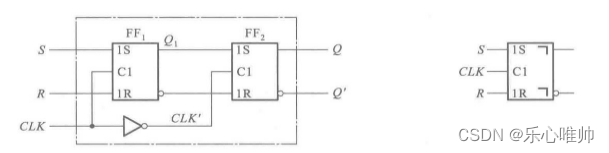
脉冲触发一般是两个电平触发连在一起。

脉冲触发时，触发器的翻转分为两步动作。

假设从触发器的输入端C1没有小圆圈，即如上图所示。

第一步，当clk信号有效电平（需要根据主触发器的类型判断，图中为clk=1）到来后，主触发器接受输入信号、从触发器的输出状态保持不变；

第二步，当clk信号的下降沿到来后，从触发器按照主触发器的状态翻转为新的状态。

尤其注意的是，由于主触发器的输入端一般是电平触发的触发器，在有效电平时间里的全部时间里输入信号的变化都会影响主触发器的输出状态，所以必须根据有效电平时间输入信号的变化过程确定clk下降沿到来后从触发器的次态。

假设从触发器的输入端C1有小圆圈。

第一步，当clk信号有效电平（需要根据主触发器的类型判断）到来后，主触发器接受输入信号、从触发器的输出状态保持不变；

第二步，当clk信号的上升沿到来后，从触发器按照主触发器的状态翻转为新的状态。

尤其注意的是，由于主触发器的输入端一般是电平触发的触发器，在有效电平时间里的全部时间里输入信号的变化都会影响主触发器的输出状态，所以必须根据有效电平时间输入信号的变化过程确定clk上升到来后从触发器的次态。

总结一句话就是，从触发器的次态取决于主触发器的输出，而主触发器的状态会在整个电平信号中变化，所以需要对整个电平信号的主触发器的状态进行分析，再根据得到的状态判断次触发器的次态。

在脉冲触发中，需要额外记住的一个点是：在脉冲触发的JK触发器中，当clk在有效点评期间输入信号多次改变时，主触发器只翻转一次，一旦翻转后不可能再翻转回来；而脉冲触发的SR触发器中，在clk的有效电平期间主触发器可能随输入信号的变化发生多次翻转。

题型

一般是给定输入信号的波形，求对应的输出波形。

1、直接给出了触发器输入信号的波形

根据触发器的特性表和触发方式，直接就可以确定每个时钟信号周期后输出的状态。

2、输入信号经另外的组合逻辑电路加到触发器的输入端

方法一：先求出每个输入端的波形图。

方法二：如果输入端输入信号比较复杂，可以先写出输入端输入信号的逻辑函数式，然后代入触发器的特性方程，得到触发器的状态方程，再按时序判断输出、画图。

3、触发器的信号输入端（同步输入端）和异步输入端（异步置0端或异步置1端）同时有输入信号

异步置0信号R和异步置1信号S不受时钟信号控制，所以只要出现S=1，Q就置1；只要出现R=1，Q就置0.

在没有异步输入端有效信号时，处理方法同1、2。

三、存储器扩容

作业：5.1

第六章时序逻辑电路

时序逻辑电路=组合逻辑电路+存储电路

一、分析由触发器和门电路组成的时序逻辑电路

方法步骤：

写出存储电路中每个触发器的驱动方程（即触发器输入信号的逻辑函数式）。
将驱动方程带入触发器的特性方程，得到每个触发器的状态方程。
从逻辑电路图直接写出电路的输出方程。
可进一步求出电路的状态转换表，再画出状态转换图或时序图。

二、分析由中规模集成时序逻辑电路组成的时序电路（了解）

三、用触发器和门电路设计时序逻辑电路

方法步骤：

1、逻辑抽象,得到电路的状态转换图或状态转换表

①确定输人变量、输出变量和电路应有的状态数。

通常都是以事件的原因作为输入变量，以事件的结果作为输出变量。电路的状态数应包括事件发生的全部过程中所有可能出现的状态数。

②定义输入，输出逻辑状态(0和1)以及每个电路状态所代表的物理意义，并将电路状态编码。

③找出每个电路状态在不同输入条件下产生的输出和电路的次态，这样就可以画出电路的状态转换图或列出状态转换表了。

2、状态化简

若两个状态在相同输入下有相同的输出，而且转向同样的次态，则这两个状态为等价状态。

等价状态是重复的，可以合并，以减少电路的状态数。

3、状态分配

①计算存储器中触发器应有的数目。

因为电路的状态是用存储电路中触发器状态的不同组合表示的，所以首先必须算出触发器应有的数目。

②给每个电路状态规定一个对应的代码。

由于存储电路中触发器的每一组状态组合都组成一组二进制代码，所以我们在规定每个电路状态对应的触发器状态组合时，也就等于给它规定了一个代码。

4、选定触发器逻辑功能的类型，求出电路的状态方程、驱动方程和输出方程

不同逻辑功能的触发器在输入的给出方式、次态随输入和现态变化的规则是有区别的。不难想象,采用不同逻辑功能的触发器所设计出来的电路也是不一样的。因此，在设计具体电路前必须选定触发器逻辑功能的类型。一般用D触发器，老师说的，因为这样比较简单。

选定触发器类型以后，根据已经得到的状态转换图和状态编码，可以画出表示电路次态和输出的卡诺图，并进而从卡诺图写出状态方程和输出方程，再从状态方程找出驱动方程。

5、根据得到的方程组画出对应的逻辑图

6、检查所设计的电路能否自启动

当存储电路的全部状态数(也就是触发器所有的状态组合数)大于描述时序电路工作过程所需要的状态数时，必然存在着没有利用的状态。这些状态称为无效状态。

在刚一接通电源或者存在外界干扰的情况下，电路可能会进入某个无效状态。

如果在时钟信号作用下，电路最终能够进入有效状态，则这个电路就是能自启动的。反之,如果电路一旦进入无效状态后，在时钟信号作用下始终不能进人有效状态，它就是不能自启动的。

当然，假若存储电路的全部状态数和描述电路工作过程所需要的状态数相等，将不存在无效状态，自然也就不存在电路不能自启动的问题了。

四、用中规模集成的计数器设计任意进制计数器

若已有N进制中规模集成的计数器，需要设计一个M进制计数器，这时可能遇到两种情况，即N>M和N<M。

1.N>M的情况

只要设法在N进制计数器的计数过程中跳过N-M个状态就可以了。

跳过N-M个状态的方法有两种。

①置零法

置零法的基本原理是当计数器从全0状态（计数器中所有的触发器都是0状态）开始计数，经过M-1个状态以后，设法产生一个置零信号，使计数器的下一个状态返回全0状态，这样就跳过了N-M个状态，从而得到了M进制计数器。

采用置零法时有两点需要特别注意，否则解题时很容易发生错误，这就是：

对于异步置零方式和同步置零方式的器件，置零信号的产生方法是不同的。
可能需要另外译出进位输出信号

②置数法

置数法的基本原理：在已有N进制计数器的状态循环中，取任意一个状态为起始状态开始计数，经过M-1个状态以后，设法产生一个预置数信号，将计数器重新置为起始状态，这样就跳过了N-M个状态而得到了M进制计数器。

采用置数法设计任意进制计数器时同样要特别注意两个问题：

不同类型的计数器当中预置数的操作也有异步和同步之分，因而产生预置数信号的方法也是有区别的。
如果所设计的计数器在计数过程中跳过了产生进位输出的状态，那么进位输出端将没有输出信号，必须另外译出进位输出信号。

2.N<M的情况

这时可以用两个(不够时可以用3个或者更多个)N进制计数器串接起来得到一个NxN进制的计数器，使N×N>M，然后利用置零法或置数法，将这个NXN进制计数器改接为M进制计数器。

在M可以分解为两个小于N的因数a和b相乘时，也可以先将两个N进制计数器分别改接为a进制和b进制的计数器,然后将这两个a进制计数器和b进制计数器串接，得到M进制计数器。

五、用Verilog HDL语音描述时序逻辑电路

用Verilog HDL语言描述同步时序电路，也就是对有限状态机进行描述。

在描述时，可以参照同步时序电路的三组方程进行。

在三组方程中，驱动方程和输出方程是组合电路，可以用一个always模块进行描述；

状态方程界定了状态间的转换，由时钟边沿触发每一次转换，用另一个 always模块描述。

这也是用Verilog HDL语言描述时序电路最常见的二段式。

作业：6.31、6.11、6.12、6.3

第七章有限状态机

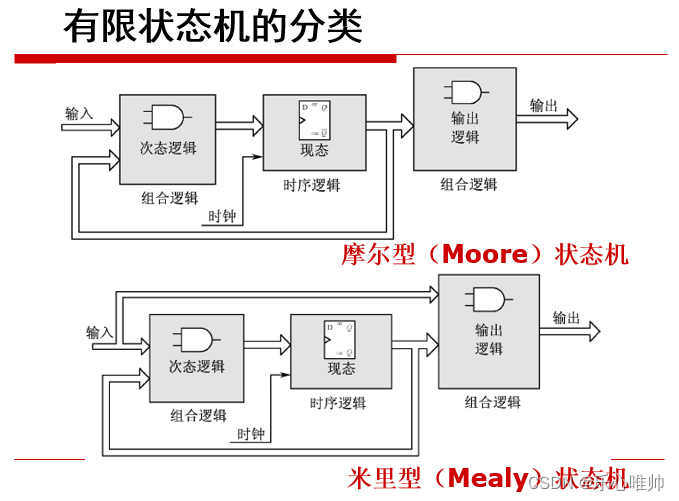
有限状态机简称状态机，是表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。

有限状态机是时序电路设计中经常采用的一种方式，尤其适于设计数字系统的控制模块。

用Verilog的case、if-else等语句能很好地描述基于状态机的设计。

一、有限状态机的分类

二、有限状态机的几种描述方式

（1）用三个过程描述：即现态（CS）、次态（NS）、输出逻辑（OL）各用一个always过程描述。

（2）双过程描述（CS+NS、OL双过程描述）：使用两个always过程来描述有限状态机，一个过程描述现态和次态时序逻辑（CS+NS）；另一个过程描述输出逻辑（OL）。

（3）双过程描述（CS、NS+OL双过程描述）：一个过程用来描述现态（CS）；另一个过程描述次态和输出逻辑（NS+OL）。

（4）单过程描述：在单过程描述方式中，将状态机的现态、次态和输出逻辑（CS+NS+OL）放在一个always过程中进行描述。

例：“101”序列检测器

三过程描述

/*三个always过程*/
module fsm1_seq101(clk,clr,x,z);
input clk,clr,x; output reg z; 
reg[1:0] state,next_state;
parameter S0=2'b00,S1=2'b01,S2=2'b11,S3=2'b10;
   	/*状态编码，采用格雷（Gray）编码方式*/
always @(posedge clk or posedge clr)
 /*该过程定义当前状态*/
begin	if(clr) state<=S0;        
//异步复位，s0为起始状态
		else state<=next_state;
end
		
always @(state or x) 		/*该过程定义次态*/
begin
    case (state)
	S0:begin if(x) next_state<=S1;
	         else  next_state<=S0; end
	S1:begin if(x) next_state<=S1;
	         else next_state<=S2; end
    S2:begin if(x) next_state<=S3;
             else next_state<=S0; end
    S3:begin if(x) next_state<=S1;
	         else next_state<=S2; end
    default: next_state<=S0; 	/*default语句*/
	endcase
end

always @(state) 			
/*该过程产生输出逻辑*/
begin  case(state)
		S3: z=1'b1;
		default:z=1'b0;
       endcase
end
endmodule

双过程描述1

//  “101”序列检测器（CS＋NS，OL双过程描述）。
module fsm2_seq101(clk,clr,x,z);
input clk,clr,x; output reg z; reg[1:0] state;
parameter 	S0=2'b00,S1=2'b01,S2=2'b11,S3=2'b10;
    	/*状态编码，采用格雷（Gray）编码方式*/
always @(posedge clk or posedge clr) 		/*该过程定义起始状态*/
begin	if(clr) state<=S0;        			//异步复位，s0为起始状态
		else case(state)
		S0:begin if(x) 		state<=S1;
					else   	state<=S0; end
		S1:begin	if(x) 	state<=S1;
					else   	state<=S2; end
		S2:begin
			if(x) 	state<=S3;
			else 	state<=S0; end
		S3:begin
			if(x) 	state<=S1;
			else 	state<=S2; end
		default:	state<=S0;
	endcase
end
always @(state) 			//该过程产生输出逻辑（OL）
begin  case (state)
		S3: z=1'b1;
		default:z=1'b0;
endcase
end
endmodule

双过程描述2

//  “101”序列检测器（CS，NS＋OL双过程描述）。
module fsm3_seq101(clk,clr,x,z);
input clk,clr,x; output reg z; reg[1:0] state,next_state;
parameter 	S0=2'b00,S1=2'b01,S2=2'b11,S3=2'b10;
    							/*状态编码，采用格雷（Gray）编码方式*/
always @(posedge clk or posedge clr) 	/*该过程定义起始状态*/
begin	if(clr) state<=S0;        			//异步复位，s0为起始状态
			else state<=next_state;
end
always @(state or x) 						/*该过程实现状态的转换*/
begin	case(state)
			S0:begin if(x) 	begin next_state<=S1; z=1'b0;end
					else  	begin next_state<=S0; z=1'b0;end
             end
			S1:begin if(x) 	begin next_state<=S1; z=1'b0;end
					else   	begin next_state<=S2; z=1'b0;end
              end
			S2:begin	if(x) begin next_state<=S3; z=1'b0;end
					else 	begin next_state<=S0; z=1'b0;end
             end
			S3:begin	if(x) begin next_state<=S1; z=1'b1;end
					else 	begin next_state<=S2; z=1'b1;end
             end
			default:		begin next_state<=S0; z=1'b0;end
	    endcase
end
endmodule

单过程描述

/*单过程描述*/
module fsm4_seq101(clk,clr,x,z);
input clk,clr,x; output reg z; reg[1:0] state;
parameter 	S0=2'b00,S1=2'b01,S2=2'b11,S3=2'b10;
/*状态编码，采用格雷（Gray）编码方式*/
always @(posedge clk or posedge clr)
Begin     if(clr) state<=S0;        //异步复位，s0为起始状态
	else case(state)
	S0:begin 	if(x) begin state<=S1; z=1'b0;end
		else begin state<=S0; z=1'b0;end
             end
	S1:begin 	if(x) begin state<=S1; z=1'b0;end
			else begin state<=S2; z=1'b0;end
              end
	S2:begin	if(x) begin state<=S3; z=1'b0;end
			else begin state<=S0; z=1'b0;end
             end
	S3:begin  if(x) begin state<=S1; z=1'b1;end
			else begin state<=S2; z=1'b1;end
             end
	default:begin  state<=S0; z=1'b0;end   /*default语句*/
	endcase
end
endmodule

三、有限状态机设计要点

1、起始状态的选择

起始状态是指电路复位后所处的状态，选择一个合理的起始状态将使整个系统简洁、高效。多数EDA软件会自动为基于状态机的设计选择一个最佳的起始状态。

2、有限状态机的同步复位

在时钟跳变沿复位。

3、有限状态机的异步复位

在上电或者系统错误时复位，采用异步复位比较好。

四、处理多余状态的方法

在case语句中用default分支决定如果进入无效状态所采取的措施；
编写必要的Verilog源代码明确定义进入无效状态所采取的行为。

作业：“10011”序列检测有限状态机

module test(clk,x,z)
input clk;
input x;
output reg z;

parameter s0=0,s1=1,s2=2,s3=3,s4=4,s5=5;
reg[2:0] cs,ns;


//分频
reg clk1;
reg[21:0] count;
always@(posedge clk)
    begin
        if(count==24999999)
            count<=0;
        else
            count<=count+1;
    end

//状态设置
always@(posedge clk or negedge reset)
    begin
        if(!reset)
            cs=s0;
        else
            cs=ns;
    end


//状态机
always@(cs,x)
    begin
        case(cs)
            s0:if(x) ns=s1; else ns=s0;
            s1:if(x) ns=s1; else ns=s2;
            s2:if(x) ns=s1; else ns=s3;
            s3:if(x) ns=s4; else ns=s0;
            s4:if(x) ns=s5; else ns=s2;
            s5:if(x) ns=s1; else ns=s2;
            default:ns=s0;
    end


//输出
always@(cs)
    begin
        if(cs==s5)
            z<=1;
        else
            z<=0;
    end

endmodule

以上就是数字逻辑与eda技术的理论部分，Verilog 语法与实验部分见另两个博客。

最后

以上就是传统招牌为你收集整理的【数字逻辑与EDA技术】数字电子技术基础-期末考试重点总结第一章数制和码制第二章、逻辑代数基础第三章门电路第四章组合逻辑电路第五章半导体存储电路第六章时序逻辑电路第七章有限状态机的全部内容，希望文章能够帮你解决【数字逻辑与EDA技术】数字电子技术基础-期末考试重点总结第一章数制和码制第二章、逻辑代数基础第三章门电路第四章组合逻辑电路第五章半导体存储电路第六章时序逻辑电路第七章有限状态机所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：数字逻辑与EDA技术
浏览次数：59 次浏览
发布日期：2023-05-14 01:54:01
本文链接：https://www.kaopuke.com/article/k-p-k_14_ujo_2_f0_14__7__2_z.html

【数字逻辑与EDA技术】数字电子技术基础-期末考试重点总结第一章 数制和码制第二章、逻辑代数基础第三章 门电路 第四章 组合逻辑电路第五章 半导体存储电路 第六章 时序逻辑电路第七章 有限状态机

概述

第一章 数制和码制