基于LSCF和LSFD算法在频域中识别快速实现的MIMO研究附Matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

????个人主页：Matlab科研工作室

????个人信条：格物致知。

更多Matlab仿真内容点击????

智能优化算法  神经网络预测 雷达通信  无线传感器

信号处理 图像处理 路径规划 元胞自动机 无人机  电力系统

⛄ 内容介绍

该工具允许使用 MIMO 系统的复杂频率响应函数 (FRF) 来识别模态参数、特征频率、模态阻尼因子和模态留数。使用基于fft的正规方程的快速实现来解决最小二乘问题，以提高算法的效率。

⛄ 部分代码

function [fn, xin, frfnumtot, FST, FF, XIXI, MATHP] = lscf(w, frf, n)

% Linear Square Complex Frequency estimator using discrete-time z-model

%    

%             k=n

%            ----- 

%                     k  

%            .     A z

%            /      

%            -----

%             k=0                            j k w dt

% H(z) = -------------------------,    z = e

%             k=n

%            ----- 

%                     k    

%            .     B z

%            /      

%            -----

%             k=0

%

% the frequency axis between f0 and fend is shifted using

%

%             1

% dt = --------------

%       2 (fend - f0)

%

% w = 2 pi (f - f0)

%

% w          natural frequency vector in rad/s

% frf        complex frequency response function matrix

%            each column corresponds to one FRF between one sensor

%            and one actuator

% n          [nmin : nmax] identification using stabilization chart

%

% fn         eigen frequency in Hz

% xin        modal damping factor

% frfnumtot  matrix with numerical identified complex frequency response

%            function using discrete-time z-model

% FST        cell array with frequency of stable poles in frequency and damping

% FF         cell array with frequency of stable poles in frequency

% XIXI       cell array with frequency of stable poles in damping

% MATHP      cell array with frequency of mathematical poles

%

% References:

% H. Van der Auweraer, P. Guillaume, P. Verboven and S. Vanlanduit, Application 

% of a  Fast-Stabilizing Frequency Domain Parameter Estimation Method, 

%Journal of Dynamics Systems, Measurement and Control, 123, pp 651-658, 2001.

%

%% Parameters and frequency shift

w0 = w ; % natural frequency in rad/s

L = length(w) ; % length of the signal

f = w/(2*pi) ; % frequency in Hz

yfrftot = 20*log10(abs(frf)) ;

f0 = min(f) ;

fend = max(f) ;

w = 2*pi*(f-f0) ; % shifted natural frequency

dt = 1/(2*(fend-f0)) ; % sample time

[L , noni] = size(frf) ; % noni: number output * number input

% cell array to save frequency of stable poles in frequency and damping

% at each iteration

FST = {} ; FF = {}; XIXI = {}; MATHP = {} ;

frfnumtot = zeros(L, noni) ;

disp('-----------------------------------------')

disp(['Identification between order ',num2str(n(1)),' and ',num2str(n(end))])

disp('-----------------------------------------')

n_min = min(n) ;

n_max = max(n) ;

Ptot = zeros(L, n_max+1) ;

for k=1:n_max+1

    % matrix P for normal equations using z-domain model

    Ptot(:, k) = zdomain(w, dt, k-1) ;

end

ip = 0 ;

iFST = 1 ;

%% fast implementation of normal equations using fft

% fft are padded with zeros because 2*L > L and dt=1/(2(fend-f0))

X1 = fft(frf, 2*L) ;

X2 = fft(conj(frf), 2*L) ;

% correction to avoid warning on the first term of the toeplitz matrices

X2(1,:)= X1(1,:) ;

Y1 = fft(ones(L,1), 2*L) ;

Z1 = fft(abs(frf).^2, 2*L) ;

%% calcul between n_min and n_max

P = Ptot(:, 1:n_min) ;

for p = n_min:n_max

    fn = [] ;

    xin = [] ;

    ff = [] ;

    xixi = [] ;

    mathp = [] ;

    P = cat(2, P, Ptot(:,p+1)) ;

    Xtot = {} ;

    Ytot = {} ;

    Ztot = {} ;

    Atot = {} ;

    M = zeros(p+1, p+1) ;

    % fast implementation using toeplitz matrix

    for ifrf = 1:noni

        X = toeplitz(-real(X1(1:p+1, ifrf)), -real(X2(1:p+1, ifrf).')) ;

        Y = toeplitz(real(Y1(1:p+1))) ;               

        Z = toeplitz(real(Z1(1:p+1, ifrf))) ;

        Xtot{ifrf} = X ; Ytot{ifrf} = Y ; Ztot{ifrf} = Z ;

        Mifrf = Z - X'*Y^(-1)*X ;

        M = M + Mifrf ;

    end

    M = 2*M ;

    B = lsqminnorm(-M(1:p, 1:p), M(1:p, p+1)) ;

    B = [B; 1] ;

    % calcul of frfnumtot only for the last iteration

    if p == n_max

        for ifrf = 1:1:noni

            Atot{ifrf} = -lsqminnorm(Ytot{ifrf},(Xtot{ifrf}*B)) ;

            frfnumtot(:,ifrf) = (P*Atot{ifrf})./(P*B) ;

        end

    end

    % solve eigenvalue problem using companion matrix

    poles = companion2poles(B, p, dt) ;

    % modal parameters

    wp = abs(poles) ;

    % correction of the shift frequency

    wp = wp+2*pi*f0 ;

    xip = -real(poles)./wp ;

    % reorganize modal parameters

    [wp, iwp] = sort(wp) ;

    xip = xip(iwp) ;

    fp = wp/(2*pi) ;

    % stabilization chart

    if ip == 0

        fmin1 = fp ;

        ximin1 = xip ;

    elseif ip > 0

        [fn, xin, ff, xixi, mathp] = stabchart(fp, xip, fmin1, ximin1, ...

        f, fn, xin, ff, xixi, mathp, p) ;

        xin = xin' ;

        fmin1 = fp ;

        ximin1 = xip ;

        FST{iFST} = fn ; FF{iFST} = ff ; XIXI{iFST} = xixi ; 

        MATHP{iFST} = mathp ;

        iFST = iFST+1 ;

    end

    ip = ip+1 ;

end

%% axes, label of the figure

xlim([f0 fend*(1+5/100)])

ylim([min(min(yfrftot)) max(max(yfrftot))])

xlabel('Frequency (Hz)')

ylabel('FRF (dB)')

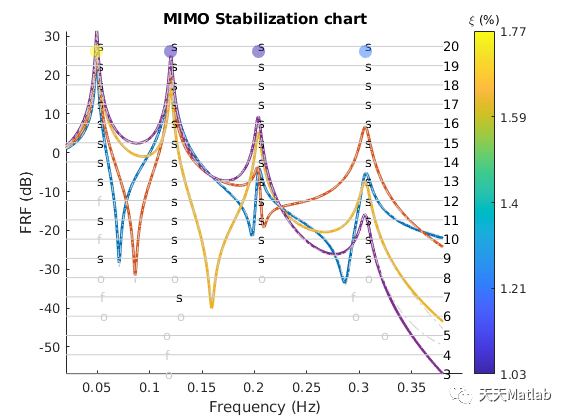
⛄ 运行结果

⛄ 参考文献

[1]王艺衡. 基于MIMO-OFDM系统的信道估计算法研究与实现[D]. 西安电子科技大学.

⛄ Matlab代码关注

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料

 

最后

以上就是炙热康乃馨为你收集整理的基于LSCF和LSFD算法在频域中识别快速实现的MIMO研究附Matlab代码的全部内容，希望文章能够帮你解决基于LSCF和LSFD算法在频域中识别快速实现的MIMO研究附Matlab代码所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。