采样时间对结果影响

90 阅读 0 评论 60 点赞

我是靠谱客的博主包容小猫咪，最近开发中收集的这篇文章主要介绍采样时间对结果影响，觉得挺不错的，现在分享给大家，希望可以做个参考。

Chirp信号在不同的采样频率下的波形

计算Chirp信号的公式在博文《Chirp信号公式与对离散生成算法之间的差异》进行了讨论。下面重新给出对应的计算公式：

${{{f_{end} - f_{start} } over {t_1 }} cdot {1 over 2}t^2 + f_{start} cdot t} right)} right]$

公式中的参数：
起始频率： $f_{start} = 250Hz$
结束频率： $f_{edn} = 2000Hz$
结束时间： $t_1 = 0.2048s$

分别使用10kHz, 200kHz的采样频率对上述信号进行采样，绘制出各自的信号波形如下：

（1）10kHz采样得到的2048个样本数据：
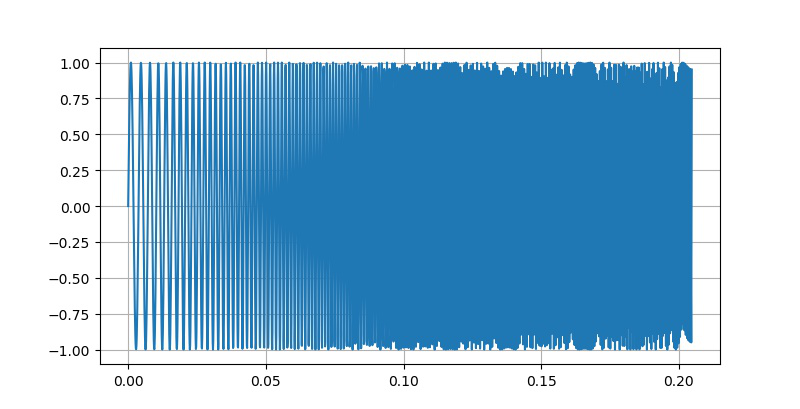
▲ 10kHz采样的波形

^{▲ 10kHz采样的波形}

（2）使用200kHz采样得到的40960个样本数据：
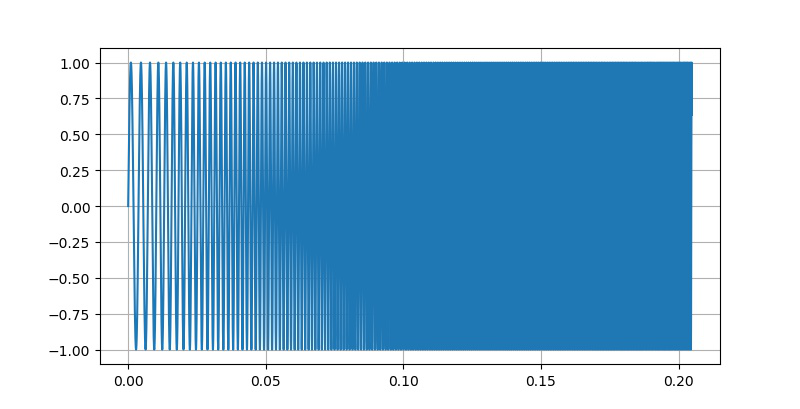
▲ 200kHz采样的波形

^{▲ 200kHz采样的波形}

对比上面两个波形可以看出，使用200kHz采样所得到的数据在波形上更加的完整。而10kHz的所得到的震荡信号的幅值在超过1000Hz之后就变得不那么整齐了。

将这两种不同采样率的波形拉开放大对比，在高频的时候，它们的差距还是蛮大的。
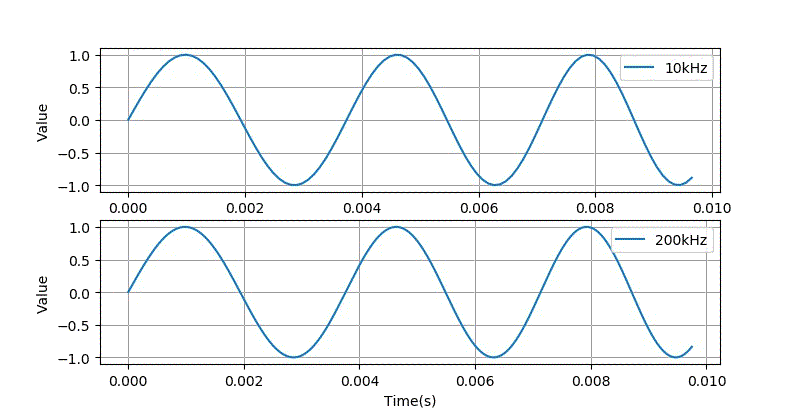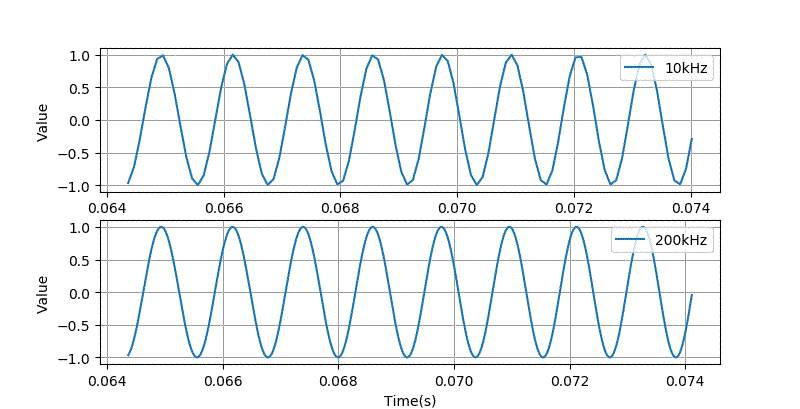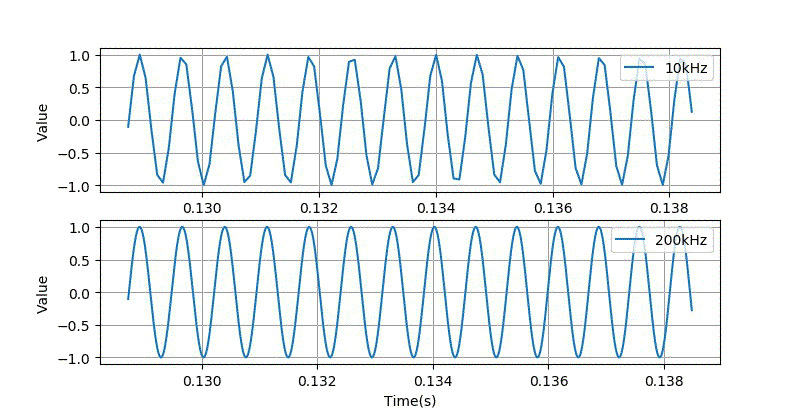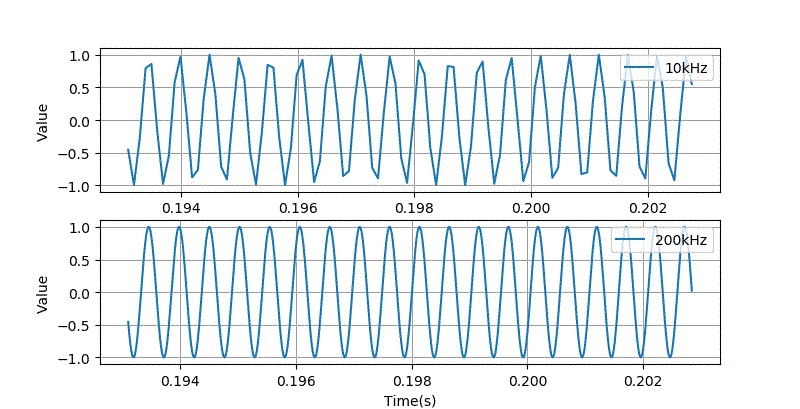
▲ 将两种不同采样率Chirp波形放大对比

^{▲ 将两种不同采样率Chirp波形放大对比}

▲ 使用10.24ms的数据进行相关所得到的波形

^{▲ 使用10.24ms的数据进行相关所得到的波形}

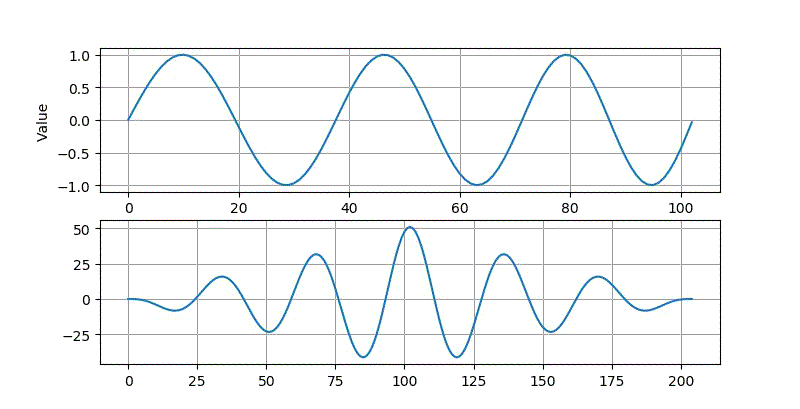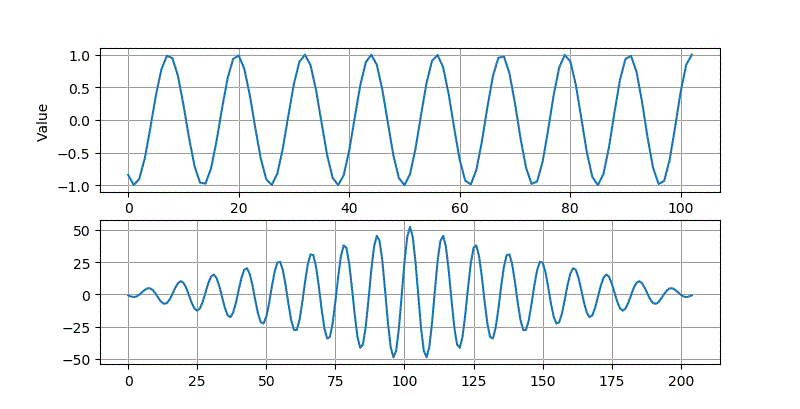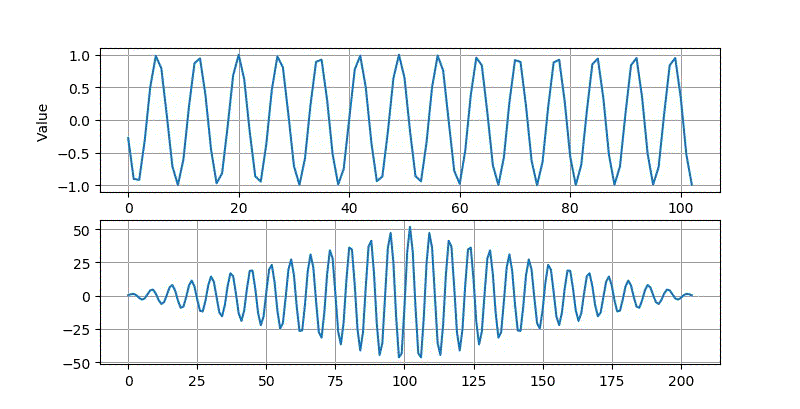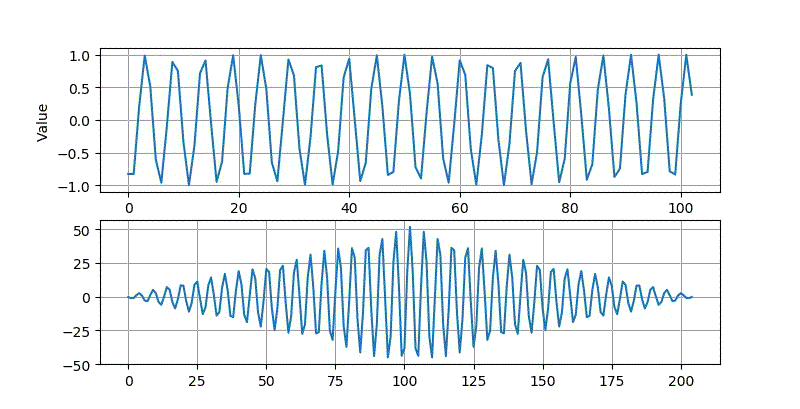
▲ 使用10.24ms的10kHz采样率数据进行相关所得到的波形

^{▲ 使用10.24ms的10kHz采样率数据进行相关所得到的波形}

以上就是包容小猫咪为你收集整理的采样时间对结果影响的全部内容，希望文章能够帮你解决采样时间对结果影响所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。