统计数据的展示

数据类型

数值型：采用某些特定的统计学方法

连续数值型：

身高、体重

离散数值型：

子女的个数：012345

分类型：其他方法

分类数据

1. 布尔变量

2. 名义变量

3. 等级变量

在python中作图

函数式和面向对象式的绘图方法

函数式

面向对象式（优势：学术上表达事情明确清晰）

交互式绘图

matplotlib交互不如Matlab直观

展示统计学数据集

seabornpandas 都是基于matplotlib

seaborn 旨在提供一个简洁、高层的接口，用于绘制富含信息扯且美观的统计学图形

pandas 提供了许多可视化数据框的方法

单变量数据

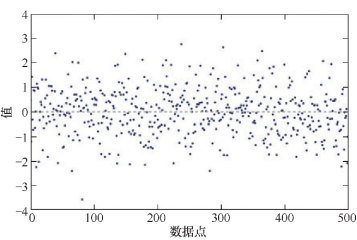
1.散点图

或

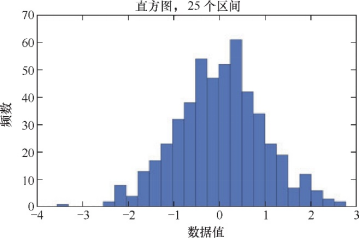
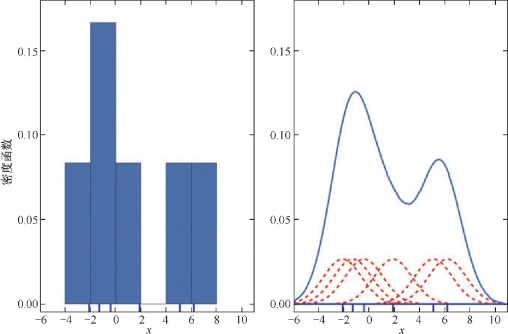
2.直方图

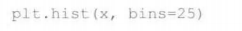
3.核密度（KDE）估计图

用正态分布解决直方图非连续的问题

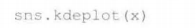
4.累积频率

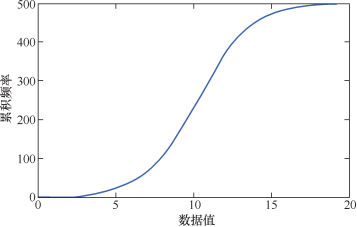
正态分布的累积频率函数

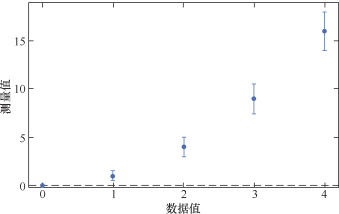
5.误差条图

使用标准误有一个很好的特性:当基于标准误的两组误差条图之间有重叠时，我们可以确定两组之间的均值没有统计学差异( p >0.05 )。反之则不一定成立!

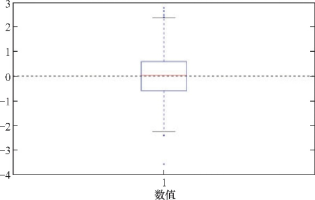
6.箱形图

箱子的底部和顶部分别表示第一分位数和第三分位数，箱子内部中间的线表示中位数，

下面的须表示在第一分位数外 1.5 x IQR (四分位距）范围内的最低值，而上面的须表示在第三分位数外

1.5 X IQR (四分位距）范围内的最高值。（另一个习惯用法是须表示了整个数据的范围。）

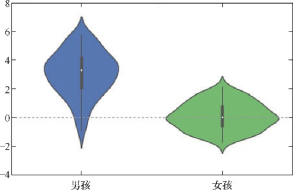
小提琴图=箱形图+核密度估计图

纵轴和箱形图一样，但是在水平方向上额外绘制了对称的核密度估计图

7.分组的条形图

8.饼图

二元变量和多元变量绘图

1.二元变量散点图

带有不同大小数据点的散点图

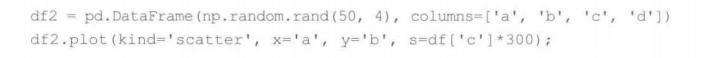
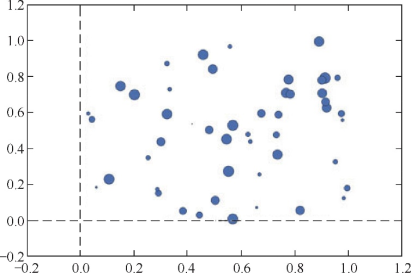
2.3D图

3D图坐标轴需要显式声明，一旦正确定义坐标轴，剩下的部分就很直观了

分布和假设检验

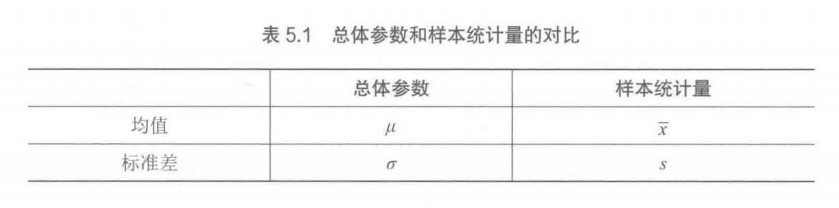
总体和样本

总体 ：包括数据集中的所有元素

样本 ：总体中的一个或多个观察值组成

参数 ：总体的特征，如均值或标准偏差（度量数据分布的分散程度）通常用希腊字母表示

统计量： 一个样本的可测量的特征

• 样本数据的均值；

• 样本数据的极差；

• 数据与样本均值的偏离

抽样分布：基于随机样本的给定统计量的概率分布

概率分布

概率密度：X为连续型随机变量，称f(x)为X的概率密度函数，简称为概率密度

概率分布：，在统计图上画出概率密度，概率分布是描述总体和样中数值数据分布的数学工具

离散分布

掷骰子

对于给定的离散分布， Pi称为该分布的概率质量函数 （PMF)

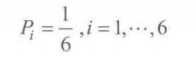
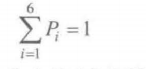
连续分布

例如，一个人的重量可以是任意正数，描述每个值的概率的曲线，即概率分布，是一个连续函数，称为概率

密度函数 (PDF）。

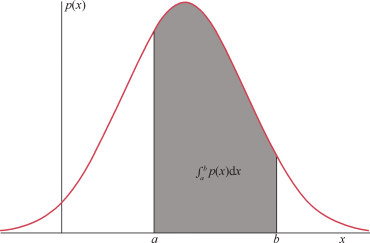
p(x) 是值 x 的概率密度函数。在 a 和 b 之间的 p(x) 上的积分表示在该范围内找到 x 的值的可能性

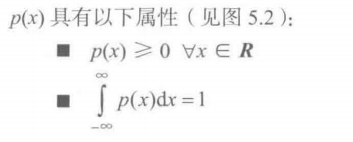
期望值和方差

1.期望值

离散分布：

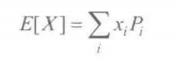
连续分布：

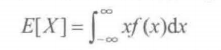
2.方差

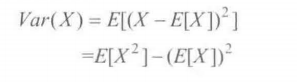
自由度Degrees of Freedom（DOF）

自由度：取值不受限制的变量个数

22个人，分三组，两组样本均值知道，总体样本均值知道，即可求出第三组样本均值，因此确定的值终于三个，自由度减三。

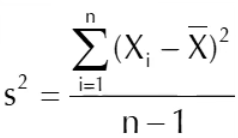
求方差，分母是自由度

研究设计

术语

因素：被控制的输入变量

协同因素：木被控制的输入变量

协变量：一个对研究结局有可能做出预测的变量，并且可以是因素或协同因素

两个输入和 个输出：

概述

单变量的分布

单变量的分布：一个变量的分布

离散分布：整数值

连续分布：浮点值

分布的特征描述

分布中心

用参数描述分布中心

1. 均值（算术均值）

受异常值影响

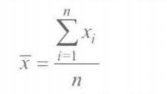
numpy

2.中位数

数据按顺序排列时中间的值，不受异常值影响

3.众数

一个分布中出现最频繁的值

4.几何均值

几何平均可以用来描述分布的位置，通过计算每个值的对数的算数平均值得到

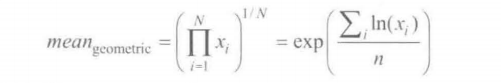
量化变异度

1.极差

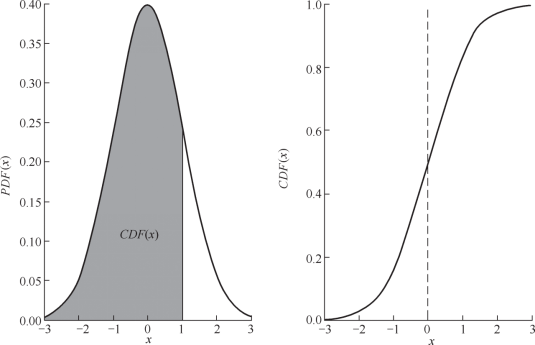
2.百分位数

CDF是PDF从负无穷大到给定值的积分

3.标准差和方差

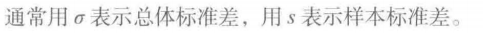
样本方差的极大似然估计（’有偏估计‘）（被除数为样本数）

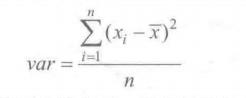
群体方差的‘无偏估计‘（被除数为自由度n-1）

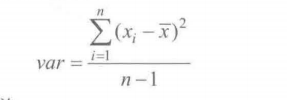
样本标准差

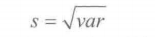
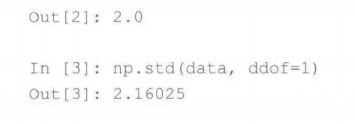
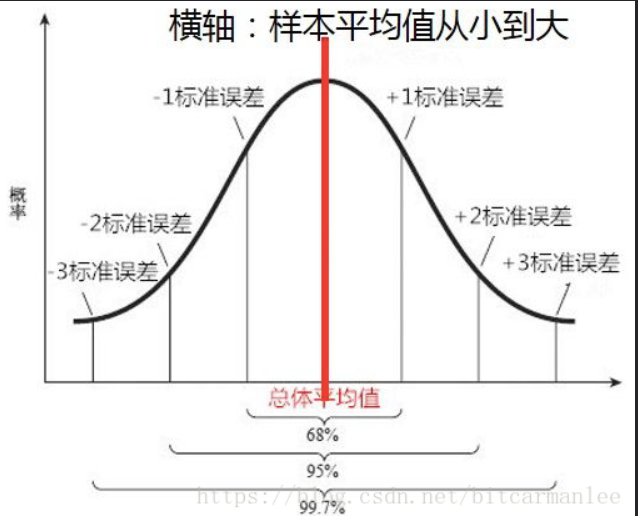
4.标准误

样本均值的标准误(Standard Error for the Sample Mean)

对一个总体多次抽样，每次样本大小都为n，那么每个样本都有自己的平均值，这些平均值的标准差叫做标准误

反映样本平均数对总体平均数的变异程度。

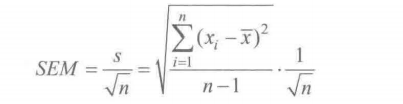
5.置信区间

[a,b]称为置信区间

a = 样本均值 - z标准误差

b = 样本均值 + z标准误差

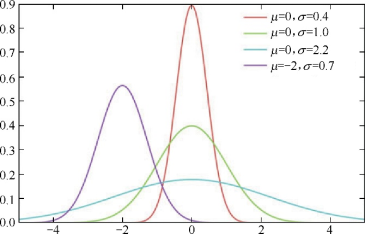
分布形状的参数描述

1.位置

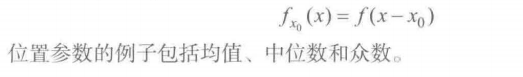
2.尺度

尺度参数描述了概率分布的宽度

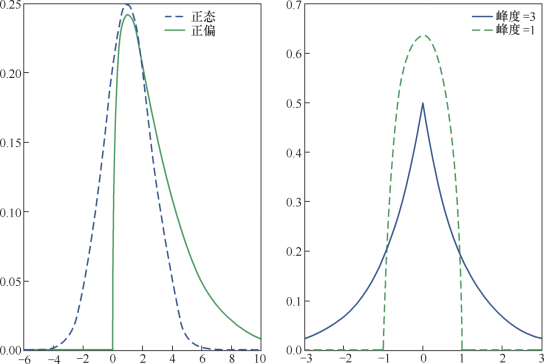
3.形状参数

偏度：标准差大于均值的一半是偏斜分布而不是正态

峰度：概率分布的’陡峭程度‘，正太分布峰度为3

离散分布

伯努利分布

抛硬币一次，是二项分布的特殊情况

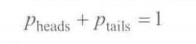
二项分布

抛硬币多次

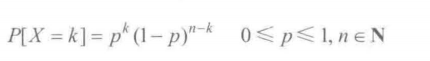
泊松分布

在连续的空间或时间内离散事件发生的次数（X为整数）

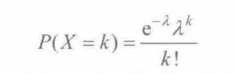
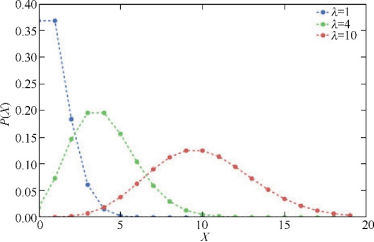
正态分布

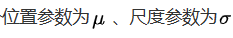
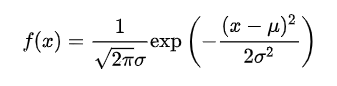
分布和假设检验

来自正态分布的连续型分布

ｔ分布：正态分布的总体中，样本均值的样本分布。通常用于小样本数且真实的均值／标准差不知道的情况。

卡方分布：用于描述正态分布数据的变异程度

F分布：用于比较两组正态分布的变异程度

ｔ分布

在大多数情况下，总体的均值和方差是未知的，我们在分析样本数据的时候一般都是处理ｔ分布

常见应用是：计算均值的置信区间

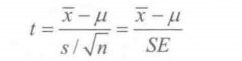
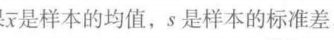
import numpy as np
from scipy import stats 
n=20
df=n-1#自由度
alpha=0.05#alpha是分位点 置信区间95%~0.05
stats.t(df).isf(alpha/2)
stats.norm.isf(alpha/2)
#均值的 95% 可信区间
alpha=0.95
df=len(data)-1
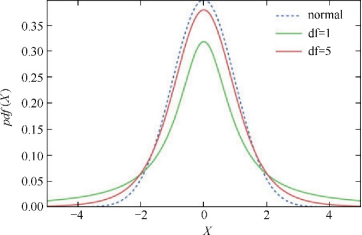
ci=stats.interval(alpha,df,loc=np.mean(data),scale=stats.sem(data))

ｔ分布的尾部比正态分布长，它更不易受极端例子影响

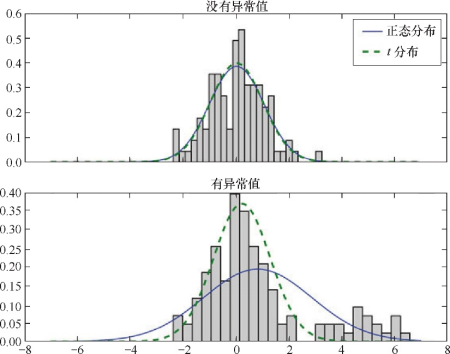
t 分布在处理异常值时比正态分布更加稳健。（上图）以来自正态分布的样本进行最佳拟合的正态分布和 t 分布。（下图）是相同的分布，但是加上了 20 个异常值，这些异常值在 5 附近呈正态分布

卡方分布

用于描述正态分布数据的变异程度

　

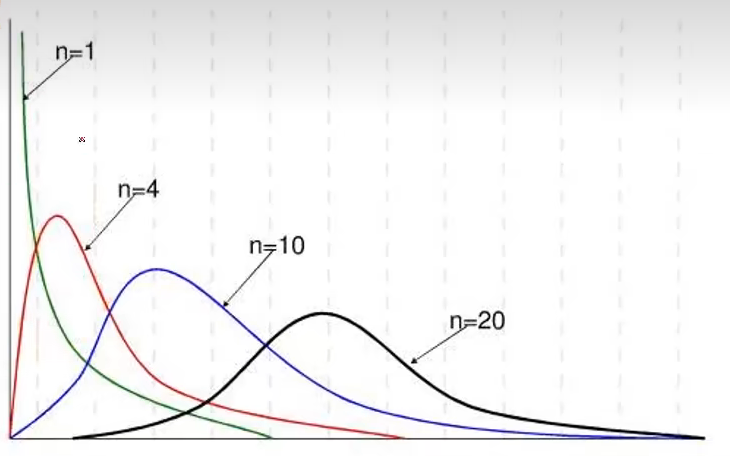
当服从正态分布的随机变量数（ｎ）越大时，自由度也越大，卡方分布图像越接近正态分布

F分布

• 比较两组正态分布的变异程度

• 方差分析

方差分析(Analysis of Variance，简称ANOVA)

又称“变异数分析”，用于两个及两个以上