学习视频：【零基础教程】老哥：数学建模算法、编程、写作和获奖指南全流程培训！

1. 线性规划的MATLAB标准形式

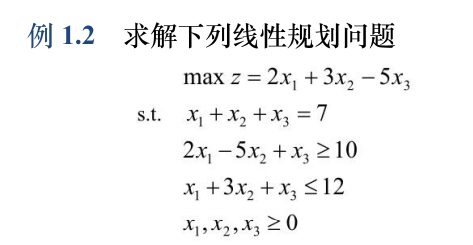
标准形式是最小值，我们要求最大值。只需要在原函数的基础上，将系数变成负数，最终求解值y也加上负号即可。

函数：linprog

f = [-2;-3;5];
a = [-2,5,-1;1,3,1];
b = [-10;12];
aeq = [1,1,1];
beq = 7;
[x,y] = linprog(f,a,b,aeq,beq,zeros(3,1));
x,y=-y

2. 整数规划问题

函数：intlinprog

intlinprog是matlab中用于求解混合整数线性规划(Mixed-integer linear programming)的一个函数，用法基本和linprog差不多

Matlab中，该模型的标注写法如下

例1：求解整数规划

例2：求解0-1规划

f=[-5 -8];
A=[1 1;5 9];
b=[6 45];
lb=zeros(2,1);
intcon=[1 2];
[x,fval]=intlinprog(f,intcon,A,b,[],[],lb,[]);
x,fval=-fval

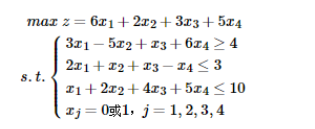
f=[-6 -2 -3 -5];
A=[-3 5 -1 -6;2 1 1 -1;1 2 4 5];
b=[-4 3 10]';
intcon=[1 2 3 4];
lb=zeros(4,1);
ub=ones(4,1);
[x,fval]=intlinprog(f,intcon,A,b,[],[],lb,ub);
x,fval=-fval

思路：在线性规划的基础上，对可行域中的解进行取整对比即可。

2.1 分枝定界法——整数规划求解

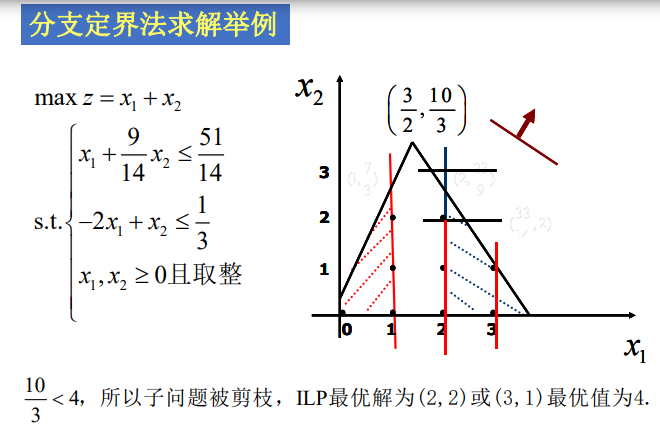
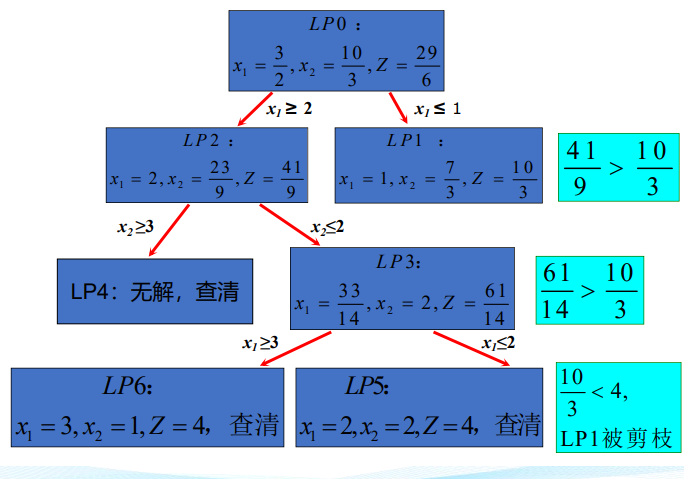
总结：对可行域内的整数解进行穷举比较。

2.2 割平面算法——整数规划求解

割平面算法

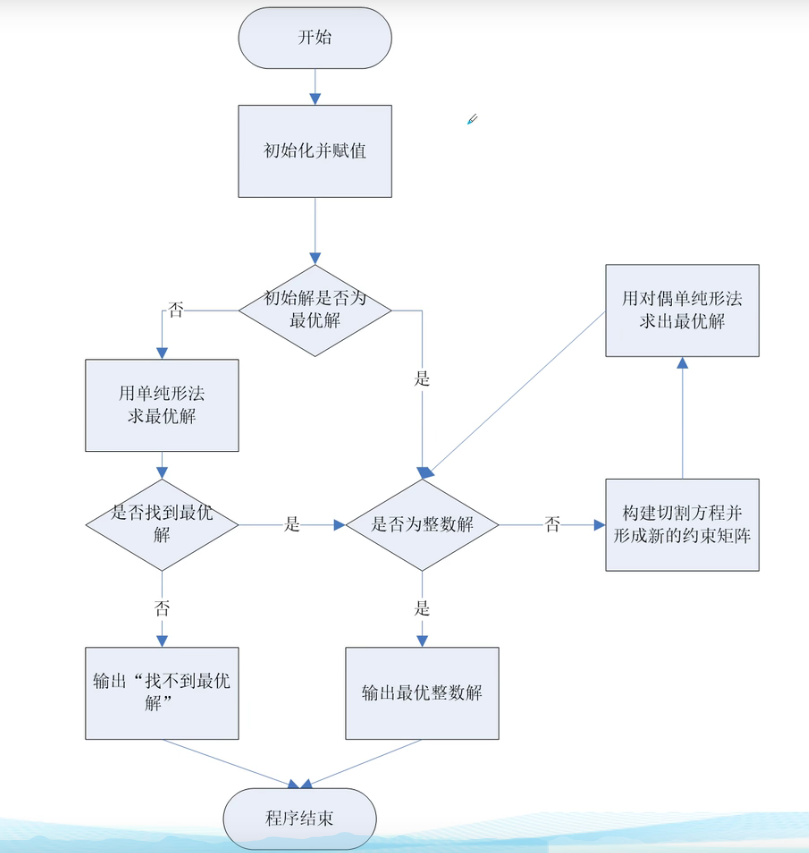
%功能：测试用割平面法求解整数规划
%调用格式：[intx,intf]=DividePlane(A,c,b,baseVector)
%其中，A：约束函数系数构成的约束矩阵；
%      c：目标函数系数向量；
%      b：约束右端向量；
%      baseVector：初始基向量；
%      intx：目标函数取最小值时的自变量值；
%      intf：目标函数的最小值；

A = [0.01 0.01 0.01 0.03 0.03 0.03 1 0 0 0;
    0.02 0 0 0.05 0 0 0 1 0 0;
    0 0.02 0 0 0.05 0 0 0 1 0;
    0 0 0.03 0 0 0.08 0 0 0 1];

c = [-20;-14;-16;-36;-32;-30];

b = [850;700;100;900];

[intx,intf] = DividePlane(A,c,b,[7 8 9 10])

2.3 匈牙利算法（0-1、分配问题）

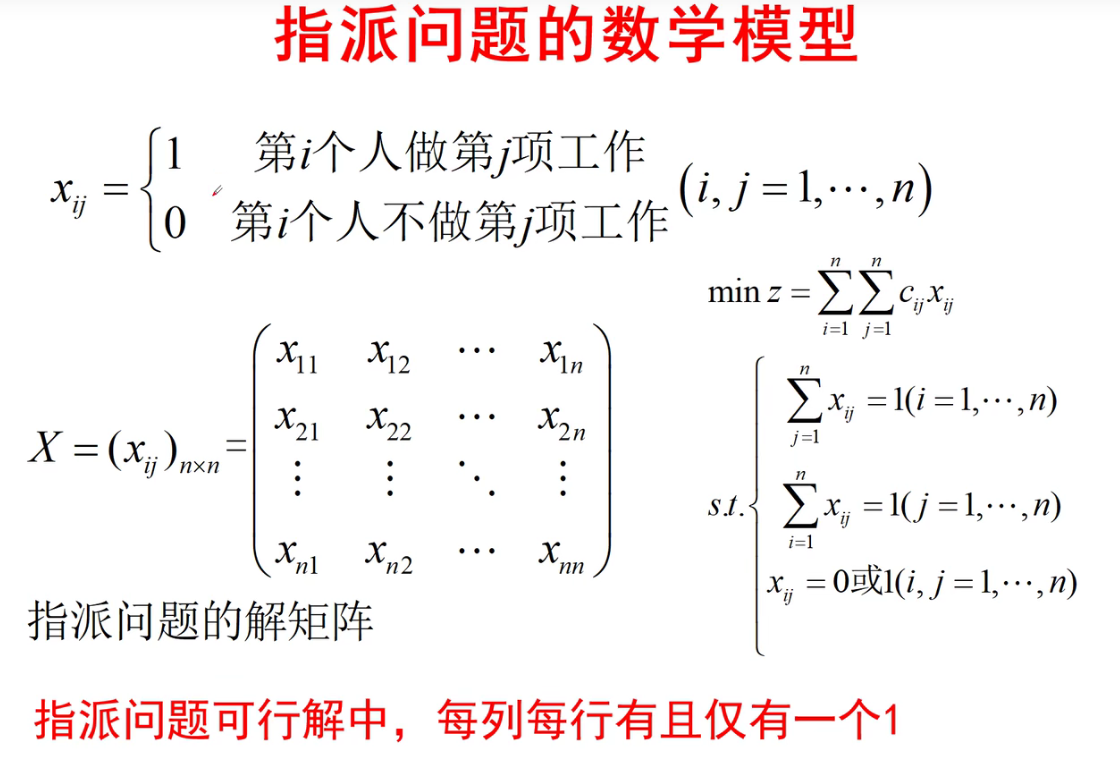
我将课件里的脚本改成了函数：

function [X,opt] = HA_fun(c,Matrix_dimensions)
%匈牙利算法解决0-1和指派问题
%   c: 输入的矩阵
%   Matrix_dimensions:矩阵的维度

c=c(:); %把矩阵c转化为向量
a=zeros(2*Matrix_dimensions,Matrix_dimensions^2);
for i=1:Matrix_dimensions %实现循环运算
    a(i,(i-1)*Matrix_dimensions+1:Matrix_dimensions*i)=1;
    a(Matrix_dimensions+i,i:Matrix_dimensions:Matrix_dimensions^2)=1;
end %此循环把指派问题转化为线性规划问题
b=ones(2*Matrix_dimensions,1);
[x,y]=linprog(c,[],[],a,b,zeros(Matrix_dimensions^2,1),ones(Matrix_dimensions^2,1));
X = reshape(x,Matrix_dimensions,Matrix_dimensions);
opt = y;

end

3. 非线性规划模型

函数：fmincon

二次规划是非线性规划的一种特殊形式。

4. 层次分析法

原理之间记过就不重复记录了：美赛笔记01_层次分析法模型

代码有很多，这里的是本节课中的代码。

% 使用方法
% （1）构造判断矩阵A
% （2）将下文代码复制粘贴到Matlab中即可
% 例如：A=[1 3 5;0.33 1 3;0.2 0.33,1]
disp('请输入准则层判断矩阵A(n阶)');
A=input('A=');
[n,n]=size(A);
[V,D]=eig(A);%求得特征向量和特征值
            %求出最大特征值和它所对应的特征向量
tempNum=D(1,1);
pos=1;
for h=1:n
    if D(h,h)>tempNum
        tempNum=D(h,h);
        pos=h;
    end
end    
w=abs(V(:,pos));
w=w/sum(w);
t=D(pos,pos);
disp('准则层特征向量w=');disp(w);disp('准则层最大特征根t=');disp(t);
         %以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59 1.60 1.61 1.615 1.62 1.63];
CR=CI/RI(n);
if CR<0.10
    disp('此矩阵的一致性可以接受!');
    disp('CI=');disp(CI);
    disp('CR=');disp(CR);
else disp('此矩阵的一致性验证失败，请重新进行评分!');
end

最后

以上就是矮小抽屉为你收集整理的MATLAB学习笔记_Day02求解线性规划（包括整数规划）、非线性规划、层次分析1. 线性规划的MATLAB标准形式2. 整数规划问题3. 非线性规划模型4. 层次分析法的全部内容，希望文章能够帮你解决MATLAB学习笔记_Day02求解线性规划（包括整数规划）、非线性规划、层次分析1. 线性规划的MATLAB标准形式2. 整数规划问题3. 非线性规划模型4. 层次分析法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。