概述
建立碰撞模型
碰撞场景
下图中，A点和D点分别表示rv和hv的中心质点，向量hv、rv的方向分别表示hv、rv的航向，hv与rv的航向夹角为
β
beta
β。以hv为坐标原点，建立载体坐标系，rv在未来的行径轨迹与x轴相交于点C，C点的坐标为
(
x
r
v
+
y
r
v
t
a
n
β
,
0
)
(x_{rv}+frac{y_{rv}}{tanbeta},text{ }0)
(xrv+tanβyrv, 0)，hv和rv到碰撞点C点的距离为
D
c
o
l
l
i
s
i
o
n
_
h
v
=
x
r
v
+
y
r
v
t
a
n
β
D
c
o
l
l
i
s
i
o
n
_
r
v
=
y
r
v
s
i
n
β
(1)
D_{collision_hv}=x_{rv}+frac{y_{rv}}{tanbeta}tag{1} \ D_{collision_rv}=frac{y_{rv}}{sinbeta}
Dcollision_hv=xrv+tanβyrvDcollision_rv=sinβyrv(1)
若hv和rv同时到达C点，那么就会发生碰撞。
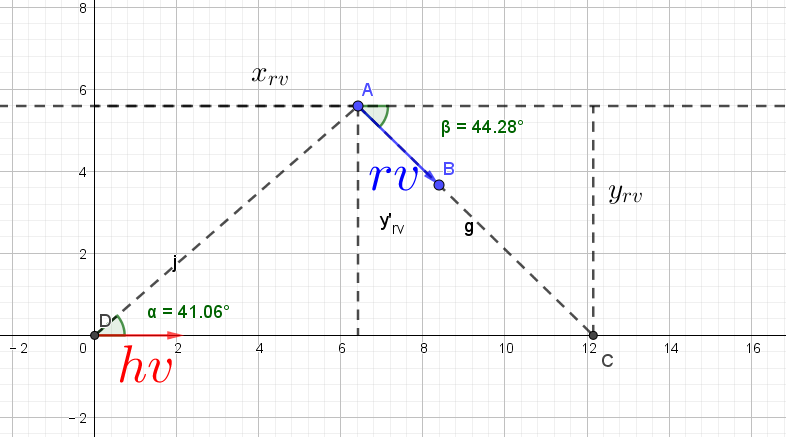
图1 交叉路口碰撞模型示意图
碰撞半径
由于在实际中，hv和rv并不是一个点，而是占有一定面积的一个矩形，因此，碰撞会发生在一个区域内。为了简化模型，这里假设碰撞区域是以C点为圆心，以
ρ
rho
ρ为半径的一个圆形区域，如下图所示：
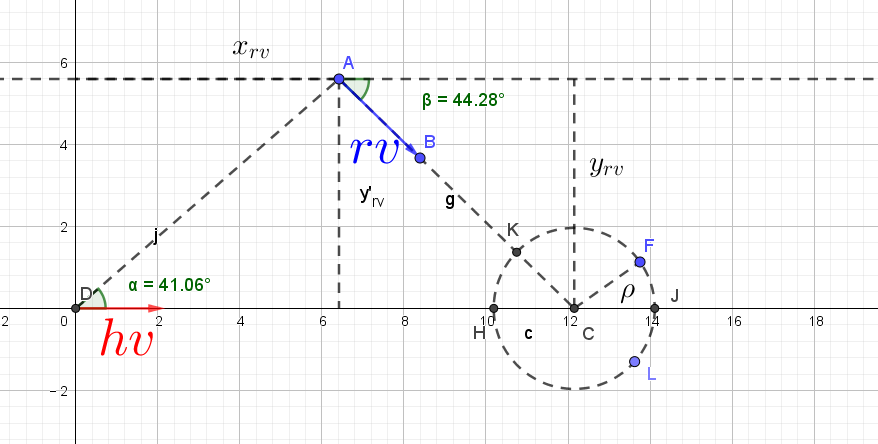
图2 碰撞半径模型
碰撞半径 ρ rho ρ受hv和rv的车长以及车宽影响，但是为了简化模型，将碰撞半径 ρ rho ρ固定为5m，即一个车长的长度。
是否会发生碰撞的条件判断
考虑到碰撞区域的存在，所以碰撞发生的临界条件可以简化为hv和rv达到和离开碰撞区域的时间。如下描述了碰撞发生的条件：
对于hv：
- hv达到碰撞区域时，rv也同时达到碰撞区域边缘；
- hv达到碰撞区域时，rv还未离开碰撞区域。
同理对于rv： - rv达到碰撞区域时，hv也同时达到碰撞区域边缘；
- rv达到碰撞区域时，hv还未离开碰撞区域。
设hv和rv达到和离开碰撞区域的时间分别为 t h v _ i n 、 t h v _ o u t 、 t r v _ i n 、 t r v _ o u t t_{hv_{in}}、t_{hv_{out}}、t_{rv_{in}}、t_{rv_{out}} thv_in、thv_out、trv_in、trv_out，则若满足如下条件：
t r v _ i n < t h v _ i n < t r v _ o u t (2) t_{rv_{in}}<t_{hv_{in}}< t_{rv_{out}}tag{2} trv_in<thv_in<trv_out(2)
或者：
t h v _ i n < t r v _ i n < t h v _ o u t (3) t_{hv_{in}}<t_{rv_{in}}< t_{hv_{out}}tag{3} thv_in<trv_in<thv_out(3)
时，表示会发生碰撞。
计算hv和rv达到和离开碰撞区域的时间
如上图2所示，hv的轨迹与碰撞区域相较于点H和点J，rv则是点K和点L，则hv、rv达到和离开碰撞区域的距离分别是：
D
h
v
_
i
n
=
D
c
o
l
l
i
s
i
o
n
_
h
v
−
ρ
=
(
x
r
v
+
y
r
v
t
a
n
β
)
−
ρ
D
h
v
_
o
u
t
=
D
c
o
l
l
i
s
i
o
n
_
h
v
+
ρ
=
(
x
r
v
+
y
r
v
t
a
n
β
)
+
ρ
D
r
v
_
i
n
=
D
c
o
l
l
i
s
i
o
n
_
r
v
−
ρ
=
y
r
v
s
i
n
β
−
ρ
D
r
v
_
o
u
t
=
D
c
o
l
l
i
s
i
o
n
_
r
v
+
ρ
=
y
r
v
s
i
n
β
+
ρ
(4)
D_{hv_{in}}=D_{collision_hv}-rho=(x_{rv}+frac{y_{rv}}{tanbeta})-rho \ D_{hv_{out}}=D_{collision_hv}+rho=(x_{rv}+frac{y_{rv}}{tanbeta})+rhotag{4} \ D_{rv_{in}}=D_{collision_rv}-rho=frac{y_{rv}}{sinbeta}-rho \ D_{rv_{out}}=D_{collision_rv}+rho=frac{y_{rv}}{sinbeta}+rho
Dhv_in=Dcollision_hv−ρ=(xrv+tanβyrv)−ρDhv_out=Dcollision_hv+ρ=(xrv+tanβyrv)+ρDrv_in=Dcollision_rv−ρ=sinβyrv−ρDrv_out=Dcollision_rv+ρ=sinβyrv+ρ(4)
假设hv和rv都是做匀速直线运动，则他们达到和离开碰撞区域的时间分别是：
t
h
v
_
i
n
=
D
h
v
_
i
n
v
h
v
t
h
v
_
o
u
t
=
D
h
v
_
o
u
t
v
h
v
t
r
v
_
i
n
=
D
r
v
_
i
n
v
r
v
t
r
v
_
o
u
t
=
D
r
v
_
o
u
t
v
r
v
(5)
t_{hv_{in}}=frac{D_{hv_{in}}}{Large{v_{hv}}} \ t_{hv_{out}}=frac{D_{hv_{out}}}{Large{v_{hv}}} \ t_{rv_{in}}=frac{D_{rv_{in}}}{Large{v}_{rv}} \ t_{rv_{out}}=frac{D_{rv_{out}}}{Large{v}_{rv}}tag{5}
thv_in=vhvDhv_inthv_out=vhvDhv_outtrv_in=vrvDrv_intrv_out=vrvDrv_out(5)
若满足公式(2)、(3)中的条件，则会发生碰撞。
若匀速直线运动会发生碰撞，则计算是应该采取加速还是减速措施
若根据公式(2)、(3)中的条件发现会发生碰撞，还应该计算加速或者减速的情况下是否可以避免碰撞。
加速计算
加速的最小安全距离是，当rv刚好达到碰撞区域边缘时，hv已经驶离了碰撞区域。由于公式(5)中已经计算出了rv达到碰撞区域的时间
t
r
v
_
i
n
t_{rv_in}
trv_in，因此这里不再计算，直接引用。hv加速时，可以认为hv以固定的加速度
a
h
v
_
a
c
c
e
a_{hv_acce}
ahv_acce做匀加速直线运动（实际计算中，加速时加速度可以取2.6
m
/
s
2
m/s^2
m/s2），因此，在
t
r
v
_
i
n
t_{rv_in}
trv_in时间内，hv运动的距离是：
S
h
v
_
a
c
c
e
=
v
h
v
t
r
v
_
i
n
+
1
2
a
h
v
_
a
c
c
e
(
t
r
v
_
i
n
)
2
(6)
S_{hv_{acce}}=v_{hv}t_{rv_in}+frac{1}{2}a_{hv_acce}(t_{rv_in})^2tag{6}
Shv_acce=vhvtrv_in+21ahv_acce(trv_in)2(6)
若满足
S
h
v
_
a
c
c
e
⩾
D
h
v
_
o
u
t
(7)
S_{hv_{acce}}geqslant D_{hv_{out}}tag{7}
Shv_acce⩾Dhv_out(7)
则表明加速后，不会发生碰撞。如不满足，则要进行减速计算。
减速计算
减速的最小安全距离是，当rv已经驶出碰撞区域后，hv还未达到碰撞区域。由于公式(5)中已经计算出了rv离开碰撞区域的时间
t
r
v
_
o
u
t
t_{rv_out}
trv_out，因此这里不再计算，直接引用。hv减速时，可以认为hv以固定的加速度
a
h
v
_
d
e
c
a_{hv_dec}
ahv_dec做匀减速直线运动（实际计算中，加速时加速度可以取6.25
m
/
s
2
m/s^2
m/s2），因此，在
t
r
v
_
o
u
t
t_{rv_out}
trv_out时间内，hv运动的距离是：
S
h
v
_
d
e
c
=
v
h
v
t
r
v
_
o
u
t
+
1
2
a
h
v
_
d
e
c
(
t
r
v
_
o
u
t
)
2
(8)
S_{hv_{dec}}=v_{hv}t_{rv_out}+frac{1}{2}a_{hv_dec}(t_{rv_out})^2tag{8}
Shv_dec=vhvtrv_out+21ahv_dec(trv_out)2(8)
若满足
S
h
v
_
d
e
c
⩽
D
h
v
_
i
n
(9)
S_{hv_{dec}}leqslant D_{hv_{in}}tag{9}
Shv_dec⩽Dhv_in(9)
则表明减速后，不会发生碰撞。
若公式(7)和(9)有一个满足，则不会发生碰撞，否则势必会发生碰撞。
最后
以上就是温婉中心为你收集整理的交叉路口碰撞预警学习笔记的全部内容，希望文章能够帮你解决交叉路口碰撞预警学习笔记所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复