数据分析之可重复与独立样本的T-Test分析

数据分析之独立样本的T-Test分析

比较两个独立样本数据之间是否有显著性差异，将实验数据与标准数据对比，查看

实验结果是否符合预期。T-Test在生物数据分析，实验数据效果验证中很常见的数

据处理方法。http://www.statisticslectures.com/tables/ttable/ - T-table查找表

独立样本T-test条件：

1.      每个样本相互独立没有影响

2.      样本大致符合正态分布曲线

3.      具有同方差异性

单侧检验(one-tail Test)与双侧检验(Two-Tail Test)

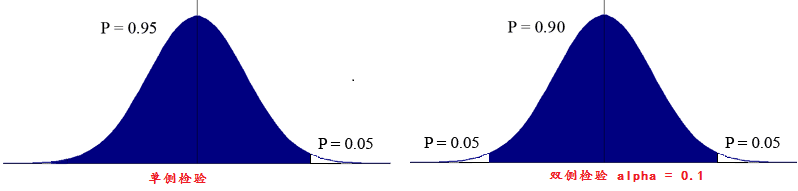
基本步骤：

1.双侧检验, 条件声明  alpha值设置为0.05

根据t-table, alpha = 0.05, df = 38时, 对于t-table的值为2.0244

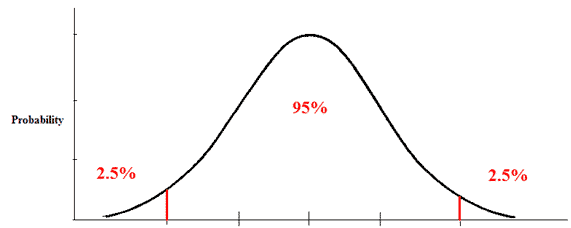
2. 计算自由度(Degree of Freedom)

Df = （样本1的总数 + 样本2的总数）- 2

3. 声明决策规则

如果计算出来的结果t-value的结果大于2.0244或者小于-2.0244则拒绝

4. 计算T-test统计值

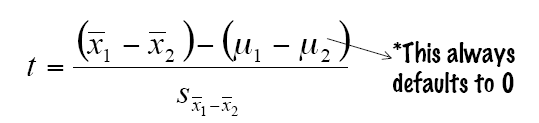
5. 得出结论

如果计算结果在双侧区间之内，说明两组样本之间没有显著差异。

可重复样本的T-Test计算

同样一组数据在不同的条件下得到结果进行比对，发现是否有显著性差异，最常见

的对一个人在饮酒与不饮酒条件下驾驶车辆测试，很容易得出酒精对驾驶员有显著

影响

算法实现：

对独立样本的T-Test计算最重要的是计算各自的方差与自由度df1与df2

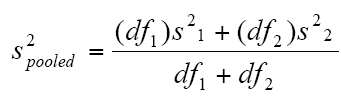
对可重复样本的对比t-test计算

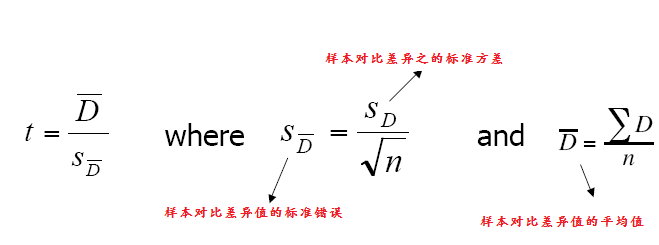
程序实现：

package com.gloomyfish.data.mining.analysis; 
        
public class TTestAnalysisAlg { 
        
    private double alpahValue = 0.05; // default 
    private boolean dependency = false; // default 
        
    public TTestAnalysisAlg() { 
        System.out.println("t-test algorithm"); 
    } 
        
    public double getAlpahValue() { 
        return alpahValue; 
    } 
        
    public void setAlpahValue(double alpahValue) { 
        this.alpahValue = alpahValue; 
    } 
        
    public boolean isDependency() { 
        return dependency; 
    } 
        
    public void setDependency(boolean dependency) { 
        this.dependency = dependency; 
    } 
        
    public double analysis(double[] data1, double[] data2) { 
        double tValue = 0; 
        if (dependency) { 
            // Repeated Measures T-test. 
            // Uses the same sample of subjects measured on two different 
            // occasions 
            double diffSum = 0.0; 
            double diffMean = 0.0; 
            int size = Math.min(data1.length, data2.length); 
            double[] diff = new double[size]; 
            for(int i=0; i<size; i++) 
            { 
                diff[i] = data2[i] -data1[i]; 
                diffSum += data2[i] -data1[i]; 
            } 
            diffMean = diffSum / size; 
            diffSum = 0.0; 
            for(int i=0; i<size; i++) 
            { 
                diffSum += Math.pow((diff[i] -diffMean), 2); 
            } 
            double diffSD = Math.sqrt(diffSum / (size - 1.0)); 
            double diffSE = diffSD / Math.sqrt(size); 
            tValue = diffMean / diffSE; 
        
        } else { 
        
            double means1 = 0; 
            double means2 = 0; 
            double sum1 = 0; 
            double sum2 = 0; 
        
            // calcuate means 
            for (int i = 0; i < data1.length; i++) { 
                sum1 += data1[i]; 
            } 
        
            for (int i = 0; i < data2.length; i++) { 
                sum2 += data2[i]; 
            } 
        
            means1 = sum1 / data1.length; 
            means2 = sum2 / data2.length; 
        
            // calculate SD (Standard Deviation) 
            sum1 = 0.0; 
            sum2 = 0.0; 
        
            for (int i = 0; i < data1.length; i++) { 
                sum1 += Math.pow((means1 - data1[i]), 2); 
            } 
        
            for (int i = 0; i < data2.length; i++) { 
                sum2 += Math.pow((means2 - data2[i]), 2); 
            } 
        
            double sd1 = Math.sqrt(sum1 / (data1.length - 1.0)); 
            double sd2 = Math.sqrt(sum2 / (data2.length - 1.0)); 
        
            // calculate SE (Standard Error) 
            double se1 = sd1 / Math.sqrt(data1.length); 
            double se2 = sd2 / Math.sqrt(data2.length); 
            System.out.println("Data Sample one - > Means :" + means1 
                    + " SD : " + sd1 + " SE : " + se1); 
            System.out.println("Data Sample two - > Means :" + means2 
                    + " SD : " + sd2 + " SE : " + se2); 
        
            // degree of freedom 
            double df1 = data1.length - 1; 
            double df2 = data2.length - 1; 
        
            // Calculate the estimated standard error of the difference 
            double spooled2 = (sd1 * sd1 * df1 + sd2 * sd2 * df2) / (df1 + df2); 
            double Sm12 = Math.sqrt((spooled2 / df1 + spooled2 / df2)); 
            tValue = (means1 - means2) / Sm12; 
        } 
        
        System.out.println("t-test value : " + tValue); 
        return tValue; 
        
    } 
        
    public static void main(String[] args) { 
        int size = 10; 
        System.out.println(Math.sqrt(size)); 
    } 
        
}

测试程序：

package com.gloomyfish.dataming.study; 
    
import com.gloomyfish.data.mining.analysis.TTestAnalysisAlg; 
    
public class TTestDemo { 
        
    public static double[] data1 = new double[]{ 
        35, 40, 12, 15, 21, 14, 46, 10, 28, 48, 16, 30, 32, 48, 31, 22, 12, 39, 19, 25 
    }; 
    public static double[] data2 = new double[]{ 
        2, 27, 38, 31, 1, 19, 1, 34, 3, 1, 2, 3, 2, 1, 2, 1, 3, 29, 37, 2 
    }; 
    public static void main(String[] args) 
    { 
        TTestAnalysisAlg tTest = new TTestAnalysisAlg(); 
        tTest.analysis(data1, data2); 
        tTest.setDependency(true); 
        double[] d1 = new double[]{2, 0, 4, 2, 3}; 
        double[] d2 = new double[]{8, 4, 11, 5, 8}; 
            
        //  The critical value for a one-tailed t-test with 
        //  df=4 and α=.05 is 2.132 
        double t = tTest.analysis(d1, d2); 
        if(t > 2.132 || t < -2.132) 
        { 
            System.err.println("Very Bad!!!!"); 
        } 
    } 
    
}